二叉排序树的理解和实现(Java)

二叉排序树的定义和性质

二叉排序树又称二叉排序树。它或者是一个空树，或者是一个具有下列性质的二叉树：

• 若它的左子树不空，则左子树上所有节点的值均小于它的根结构的值
• 若它的右子树不空，则右子树上所有结点的值均大于它的根节点的值
• 它的左、右子树也分别是二叉排序树

如下图是一个二叉排序树：



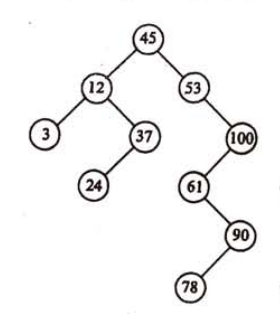
下面的代码(Java实现)基本全部基于递归实现(非递归操作复杂且效率高)，简单的实现了BST的这些操作：初始二叉排序树、查找、插入、删除任意结点、遍历二叉树(中序)。

对于二叉排序树的结点定义

public class BinaryTreeNode {

	public int data; //数据域
	public BinaryTreeNode left, right; //指向左右子节点的指针

	public BinaryTreeNode(int data, BinaryTreeNode left, BinaryTreeNode right) {
		this.data = data;
		this.left = left;
		this.right = right;
	}
}

同时，在二叉查找树实现类中定义二叉查找树的根节点：

public BinaryTreeNode root;

初始化二叉查找树

	public void insertBinaryTree(int[] datas) {

		if(datas.length < 1) {
			System.out.println("the datas Array length small zero!");
			return;
		}
		this.root = new BinaryTreeNode(datas[0], null, null);

		for (int i = 1; i < datas.length; i++) {
			this.insert(this.root, datas[i]);
		}
	}

	private void insert(BinaryTreeNode root, int data) {
		if(data > root.data) {
			if(root.right == null)
				root.right = new BinaryTreeNode(data, null, null);
			else
				this.insert(root.right, data);
		}
		else {
			if(root.left == null)
				root.left = new BinaryTreeNode(data, null, null);
			else
				this.insert(root.left, data);
		}
	}

通过传递给insertBinaryTree()存储二叉查找树值的数组来完成初始化。通过insert()方法递归的来完成对结点的初始化操作。

二叉排序树的遍历(中序)

	public void inOrder(BinaryTreeNode root) {
		if(root != null) {
			this.inOrder(root.left);
			System.out.print(root.data + "-");
			this.inOrder(root.right);
		}
	}

根据二叉排序树的特性我们知道如果根节点非空，则根节点的左子树上所有结点的值均小于根节点，右子树上的所有结点值均大于根节点。同理对任意子树都满足上面。所以对于二叉排序树的遍历是对二叉排序树的由小到大的升序输出。在这里前序和后序遍历与中序逻辑相似，不做展示。

根据键值查询BST

	public boolean SearchBST(BinaryTreeNode root, int key) {
		if(root == null) {
			return false;
		}
		else if(key == root.data) {
			return true;
		}
		else if(key < root.data) {
			return this.SearchBST(root.left, key);
		}
		else {
			return this.SearchBST(root.right, key);
		}
	}

查询操作也基于递归，查询过程和节点结点值进行比较，若成功返回true。

二叉排序树的插入操作

	public boolean InsertBST(BinaryTreeNode root, int key) {
		if(!this.SearchBST(root, key)) {
			this.insert(root, key);
			return true;
		}
		else {
			System.out.println("the key existence in BinaryTree");
			return false;
		}
	}

该操作的思路是查询带插入的key是否已经在二叉排序树中，如果不在，执行insert()方法递归的将key插入到指定的位置，如果存在，返回错误信息并结束。

但是后面在想的时候发现这段代码虽然实现很简单，但是执行步骤却很复杂：在查找是否存在时就需要遍历一次完整的二叉排序树，之后在插入时同样需要遍历一次，将key插入。所以想到了一个优化就是在查找时保存key值应该插入的结点(注意，这个时候还没有插入，所以此时结点并不是真正存在的)的父结点。这样在执行插入时将插入操作的时间复杂度将为O(1)．

二叉排序树的插入操作优化：

声明一个parent结点来用来缓存查找时查到的父节点

public BinaryTreeNode parent = null;

对查询方法做简单调整：

	public boolean SearchBST2(BinaryTreeNode root, BinaryTreeNode parent, int key) {
		if(root == null) {
			this.parent = parent;
			return false;
		}
		else if(key == root.data) {
			this.parent = root;
			return true;
		}
		else if(key < root.data) {
			return this.SearchBST2(root.left, root, key);
		}
		else {
			return this.SearchBST2(root.right, root, key);
		}
	}

首次操作时parent=null，之后保存当前查询root结点的父节点。

对插入方法做简单调整：

	public boolean InsertBST2(BinaryTreeNode root, int key) {
		if(!this.SearchBST2(root, this.parent, key)) {
			BinaryTreeNode keyNode = new BinaryTreeNode(key, null, null);
			if(this.parent == null) {
				root = keyNode;
			}
			else if(key < this.parent.data) {
				this.parent.left = keyNode;
			}
			else this.parent.left = keyNode;
			return true;
		}
		else {
			System.out.println("the key existence in BinaryTree");
			return false;
		}
	}

这样在查询操作完成后通过简单的语句便可将key插入指定的位置，而不需要在做一次递归。

删除二叉排序树的任意结点

对于二叉排序树的删除操作并不是很容易，因为我们需要保证再删除了结点后，让这棵树依旧满足二叉排序树的特性，所以在删除时就需要考虑多种情况。一般分为三种情况进行讨论。

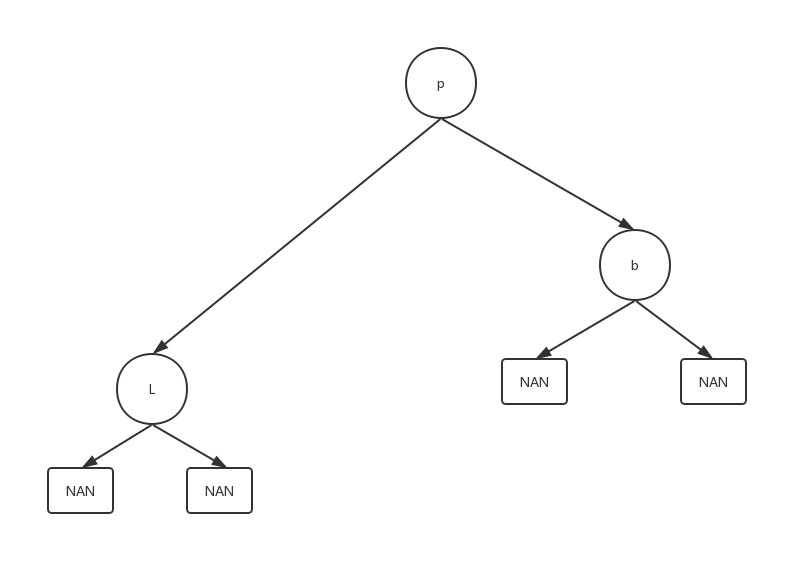
我们做一个约定：定义待删除的结点是结点x，其父结点是结点p，左子树结点是l，右子树结点是r，兄弟结点为b。其中NAN均为虚拟的null结点。

待删除的结点为叶子结点时

直接删除叶子结点x，并将父结点指向该节点的域置位NAN(null)。



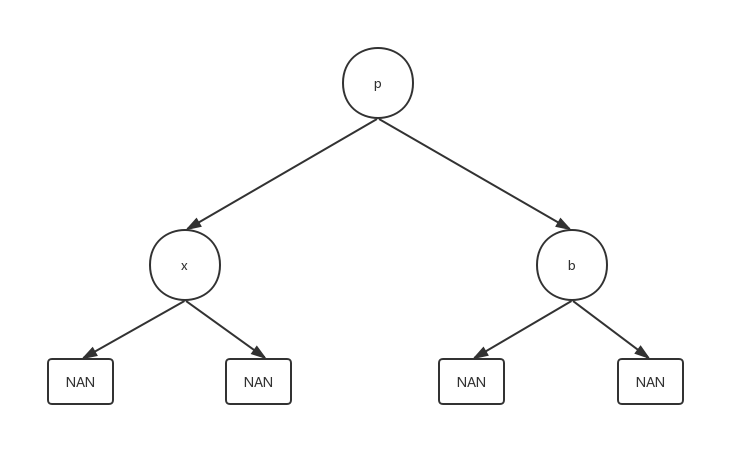
这时直接删除x结点，然后将p的左结点指向NAN结点

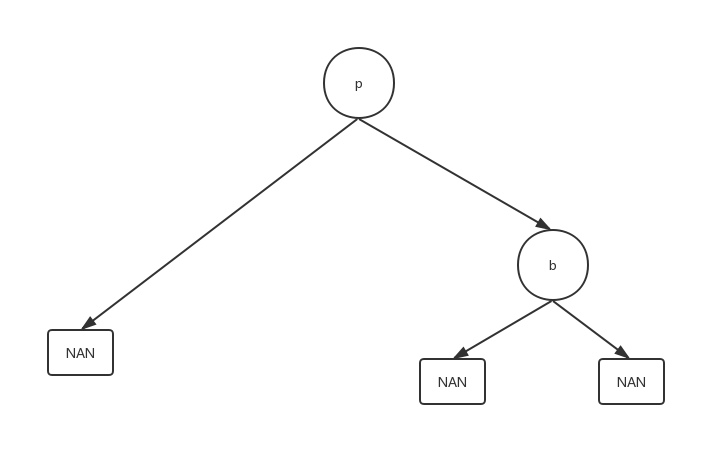
当删除的结点只有左子树或只有右子树

相对来说也好解决，那就是结点删除后，将它的左子树或右子树整个移动到删除结点的位置即可，可以理解为独子继承父业。

比如要删除结点x，直接将父结点p指向待删除的结点x的指针直接指向x结点的唯一儿子结点(l或则是r)，然后删除x结点即可。

该图只演示了删除只有左子树的结点的时候，删除只有右子树的时候思路相同。



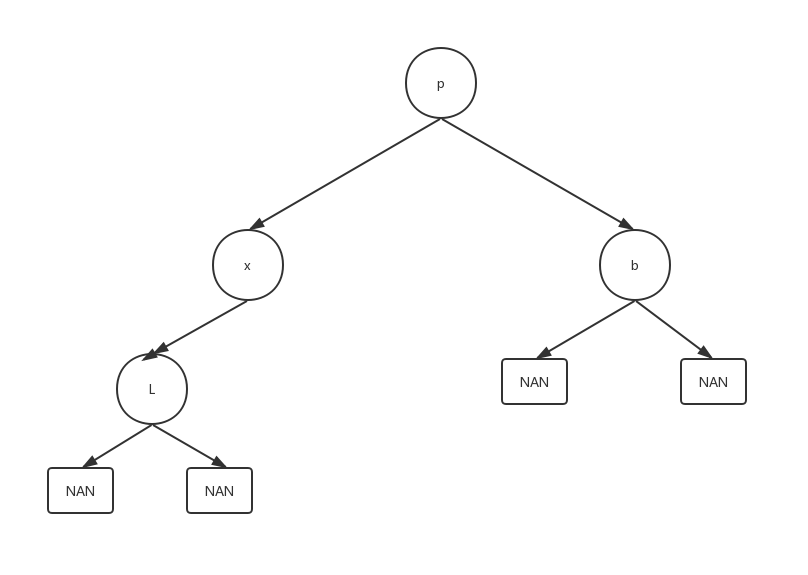
这时候将p的左子树指向x唯一的子结点L,，然后在删除x

当删除的x结点存在左右结点时

这也是最麻烦的一种情况，通常的解决方式是用删除结点x的前驱(或后继)结点填补它的位置。因为x有一个左子结点，因此它的前驱结点就是左子树中的最大结点，这样替换就能保证有序性，因为x.data和它的前驱之间不存在其他的键值。

操作如下：

1. 寻找到待删除的结点的前驱结点，并用s指向其前驱结点
2. 找到待删除结点的前驱结点的父结点，并用q来指向前驱结点的父节点。
3. 将x的前驱结点的值赋给x，完成替换操作。
4. 最后修改q的指向为s的子节点，并删除s。

递归寻找待删除的结点：

	public boolean DeleteBST(BinaryTreeNode root, int key) {

		if(root == null) {
			System.out.println("the root node is null");
			return false;
		}
		else {
			if(key == root.data) {
				return this.delete(root);
			}
			else if(key < root.data) {
				 return this.DeleteBST(root.left, key);
			}
			else {
				 return this.DeleteBST(root.right, key);
			}
		}
	}

删除指定的x结点：

	public boolean delete(BinaryTreeNode root) {
		BinaryTreeNode q, s;
		if(root.right == null) {
			root = root.left;
		}
		else if(root.left == null) {
			root = root.right;
		}
		else {
			q = root;
			s = root.left;
			while(s.right != null) {
				q = s;
				s = s.right;
			}
			root.data = s.data;
			if(q != root) {
				q.right = s.left;
			}
			else {
				q.left = s.left;
			}
		}
		return true;
	}

源代码:

public class BinaryTreeBuilder {

	public BinaryTreeNode root;
	public BinaryTreeNode parent = null;

	public void insertBinaryTree(int[] datas) {

		if(datas.length < 1) {
			System.out.println("the datas Array length small zero!");
			return;
		}
		this.root = new BinaryTreeNode(datas[0], null, null);

		for (int i = 1; i < datas.length; i++) {
			this.insert(this.root, datas[i]);
		}
	}

	private void insert(BinaryTreeNode root, int data) {
		if(data > root.data) {
			if(root.right == null)
				root.right = new BinaryTreeNode(data, null, null);
			else
				this.insert(root.right, data);
		}
		else {
			if(root.left == null)
				root.left = new BinaryTreeNode(data, null, null);
			else
				this.insert(root.left, data);
		}
	}

	public void inOrder(BinaryTreeNode root) {
		if(root != null) {
			this.inOrder(root.left);
			System.out.print(root.data + "-");
			this.inOrder(root.right);
		}
	}

	public boolean SearchBST(BinaryTreeNode root, int key) {
		if(root == null) {
			return false;
		}
		else if(key == root.data) {
			return true;
		}
		else if(key < root.data) {
			return this.SearchBST(root.left, key);
		}
		else {
			return this.SearchBST(root.right, key);
		}
	}

	public boolean SearchBST2(BinaryTreeNode root, BinaryTreeNode parent, int key) {
		if(root == null) {
			this.parent = parent;
			return false;
		}
		else if(key == root.data) {
			this.parent = root;
			return true;
		}
		else if(key < root.data) {
			return this.SearchBST2(root.left, root, key);
		}
		else {
			return this.SearchBST2(root.right, root, key);
		}
	}

	public boolean InsertBST(BinaryTreeNode root, int key) {
		if(!this.SearchBST(root, key)) {
			this.insert(root, key);
			return true;
		}
		else {
			System.out.println("the key existence in BinaryTree");
			return false;
		}
	}

	public boolean InsertBST2(BinaryTreeNode root, int key) {
		if(!this.SearchBST2(root, this.parent, key)) {
			BinaryTreeNode keyNode = new BinaryTreeNode(key, null, null);
			if(this.parent == null) {
				root = keyNode;
			}
			else if(key < this.parent.data) {
				this.parent.left = keyNode;
			}
			else this.parent.left = keyNode;
			return true;
		}
		else {
			System.out.println("the key existence in BinaryTree");
			return false;
		}
	}

	public boolean DeleteBST(BinaryTreeNode root, int key) {

		if(root == null) {
			System.out.println("the root node is null");
			return false;
		}
		else {
			if(key == root.data) {
				return this.delete(root);
			}
			else if(key < root.data) {
				 return this.DeleteBST(root.left, key);
			}
			else {
				 return this.DeleteBST(root.right, key);
			}
		}
	}

	public boolean delete(BinaryTreeNode root) {
		BinaryTreeNode q, s;
		if(root.right == null) {
			root = root.left;
		}
		else if(root.left == null) {
			root = root.right;
		}
		else {
			q = root;
			s = root.left;
			while(s.right != null) {
				q = s;
				s = s.right;
			}
			root.data = s.data;
			if(q != root) {
				q.right = s.left;
			}
			else {
				q.left = s.left;
			}
		}
		return true;
	}

	public static void main(String[] args) {
		int[] datas = {62, 88, 58, 47, 35, 73, 51, 99, 37, 93};

		BinaryTreeBuilder b = new BinaryTreeBuilder();
		b.insertBinaryTree(datas);

		b.inOrder(b.root);
		b.InsertBST(b.root, 1);
		System.out.println();
		b.inOrder(b.root);
	}
}

对于BST的总结

BST以链接方式存储，保持了链接存储结构在执行插入或删除操作时不用移动元素的优点，只要找到合适的插入和删除位置后，仅需要修改链接指针即可。插入删除的时间性能比较好。而对于BST的查找，其比较次数等于给定值的结点在二叉排序树的层数，极端情况下，最少为1次，最多不会超过树的深度。也就是说BST的查找性能取决于BST的形状。

我们希望二叉排序树是比较平衡的，其深度与完全二叉树相同，均为log⁡2n\log_{2}nlog2​n + 1，那么查找的时间复杂度也就为O(logn)，近似于折半查找。这就引申出一个问题，即如何让BST平衡化。