Spring-servlet随笔1

一：工程思想

1.建立父工程

2：导入通用依赖

3：删除无用文件

4：创建不同模块。

pom.xml 依赖文件：

<dependencies>
   <dependency>
       <groupId>junit</groupId>
       <artifactId>junit</artifactId>
       <version>4.12</version>
   </dependency>
   <dependency>
       <groupId>org.springframework</groupId>
       <artifactId>spring-webmvc</artifactId>
       <version>5.1.9.RELEASE</version>
   </dependency>
   <dependency>
       <groupId>javax.servlet</groupId>
       <artifactId>servlet-api</artifactId>
       <version>2.5</version>
   </dependency>
   <dependency>
       <groupId>javax.servlet.jsp</groupId>
       <artifactId>jsp-api</artifactId>
       <version>2.2</version>
   </dependency>
   <dependency>
       <groupId>javax.servlet</groupId>
       <artifactId>jstl</artifactId>
       <version>1.2</version>
   </dependency>
</dependencies>

二：servlet

1.子项目需要有web的支持（需要含有web.xml）

2.可以选择导入自身需要的特定依赖。

3.控制类

：java包下

：继承httpservlet 父类（本质上还是继承了servlet类）

：基本两个方法：doget 和dopost。两个方法都有两个参数，都是分别是httpservletrequest 和httpservletresponse 类型。表示接收请求和响应。

：doget（）方法中需要时1.传参。2.分装。3.转发或者重定向。

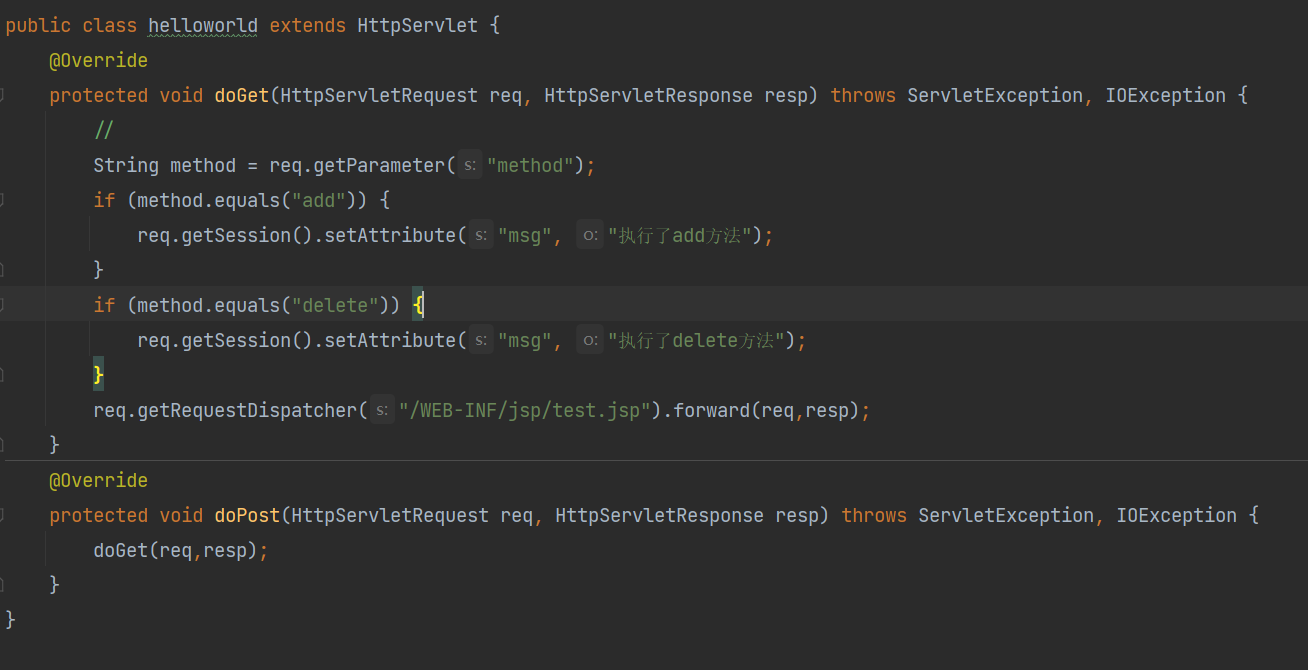
4.注册服务器servlet。

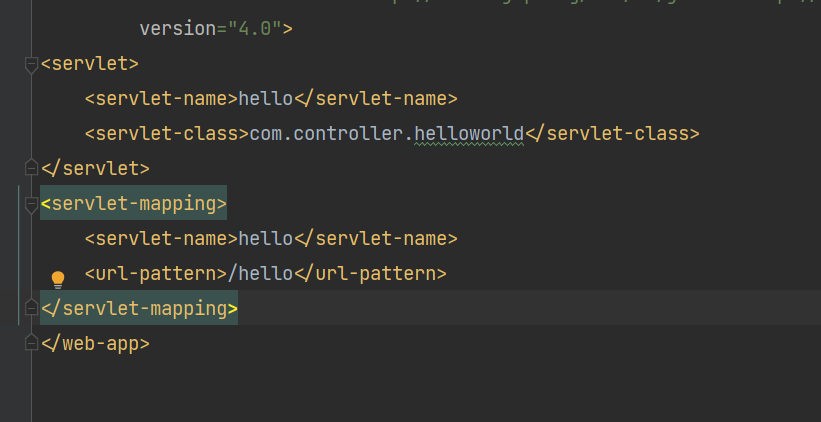
：servlet-mapping 和servlet 两个标签。

：一个是指定控制类是谁？一个是指定输入什么请求绑定哪个控制类？

：

5.index.jsp 丶web包丶jsp获取数据。

：index是在web下的，默认启动的，本身是可以根据welcome-file-list 标签来改变。

：jsp可以放在web下也可以放在web-inf下，两者的区别在于前者是公共的，没有后者安全。

：jsp获取数据${参数msg}，一般是转发的对象获取参数，而参数的内容的定义是在控制类手里。

6.Tomcat

：最好不要使用版本10.

：版本10自带了servlet-api，更改了启动文件，所以运行可能会导致实例化servlet类异常。

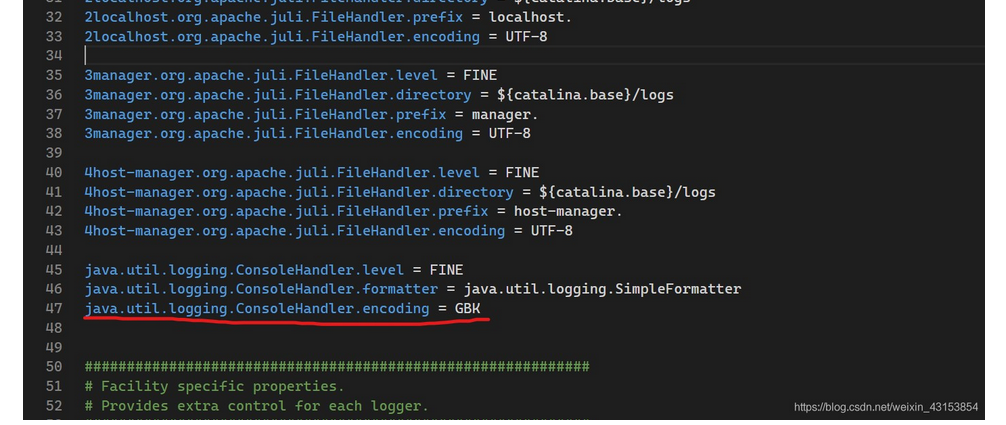
：关于安装Tomcat，无需配置环境变量，特别是含有多个tomcat，tomcat的config/logging 文件更改GBK