2020北航OO第一单元总结

前言

学习面向对象这门课程的后的第一单元作业，主线是多项式求导，三次作业层层推进，由单一的幂函数求导，到幂函数和三角函数的复合求导，最后再到两种函数的嵌套求导，由两个类到重构后的十几个类，我逐渐对面向对象的思想有了更深一步的理解，对结构化的设计也有了更加深刻的体会。

第一次作业

作业要求

实现仅含幂函数和常数的多项式求导，数据长度上限1000，性能上要求结果越短越好（即化简到最简），保证输入数据合法。

实现简述

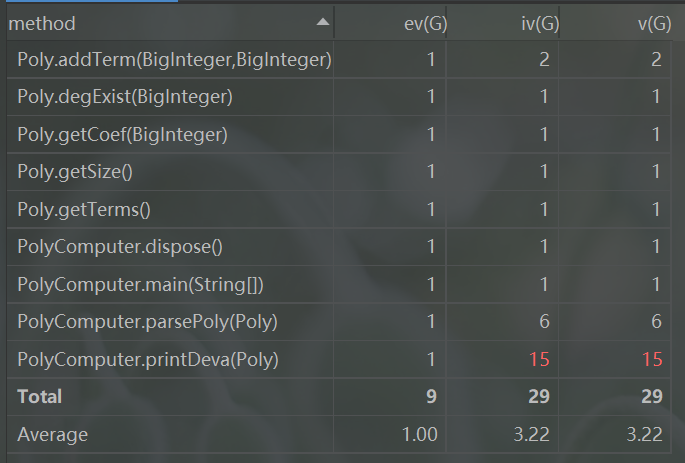
完成本次作业时，由于扩展意识不足，采取了仅为解决当前问题的设计模式，包含两个类Poly和PolyComputer，其中Poly类用一个HashMap来存储多项式每一项的系数和指数，使用BigInteger来管理系数和指数，用PolyComputer类读入字符串并进行处理，并在其中直接对求导结果进行输出，以下是我的类图分析

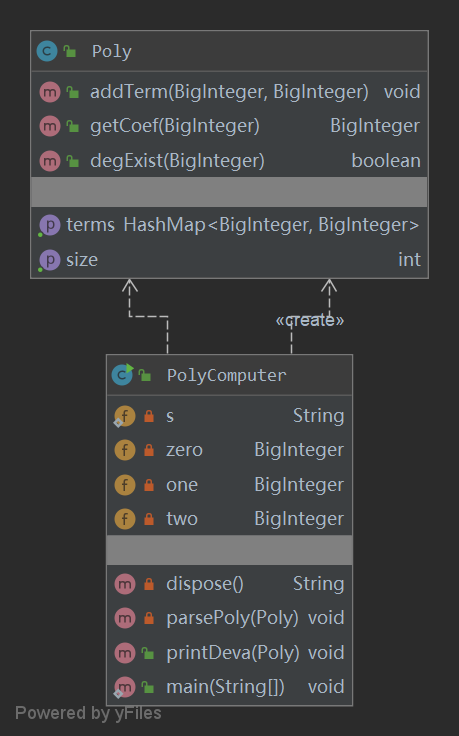
优缺点评价

优点
- 由于保证输入数据合法，在dispose处理字符串时先去掉空格并对先连的正负号进行合并，使得在parsePoly中利用正则表达式解析字符串更加简便
- 在用addTerm增加项时利用DegExist判断当前指数的项是否存在，存在就直接合并，做到了及时合并同类项
- 在printDeva输出时对系数和指数为0、±1时进行了特判，使输出结果达到较简的形式
缺点
- 在输出时的特判情况较多，易出错
- 直接对多项式进行求导，没有存储求导结果，使得printDeva与其它模块的耦合性过强，代码质量低
- 由于前期对字符串进行处理后再进行正则判断，无法适应后面需要判断格式的改变
- 未对函数设置专门类，导致代码在遇到多种函数复合求导时需要重构，扩展性低

bug分析

本次作业中，由于我在判断输出是失误，导致＞1时才输出指数，因为这一个失误下的大bug，在强测及互测阶段我被hack得很惨。当然我也进行了深刻的反思，由于第一次作业对规则还不是特别熟悉，自己在课下并没有做好充分的测试，才导致了这一bug苟过中测残留到强测及互测阶段。

在对别人的代码进行测试的过程中，我一般是构造边缘数据进行测试，如系数及指数为±1、0，连续几项相同指数需要合并，常数单一项等的情况，然后再读别人的代码进行针对性测试。最后，也成功几次hack到了别人。

第二次作业

作业要求

在第二次作业中，增加了三角函数的求导及f(x)*g(x)的复合求导形式，但三角函数因子只能为sin(x)和cos(x)，同时，也要求对输入数据进行格式判断。

实现简述

在实现本次作业过程中，由于上一次代码扩展性太差，且考虑到下次作业会更加复杂，我选择了及时重构。重构时的思路主要分为以下三个方面：

1、结构化层次关系的设计

首先，我定义了Factor类，设置系数和指数属性，在里面定义了一些因子共有的特征及加和乘的运算，然后使幂函数PowFunc和三角函数TriFunc 继承自Factor类，在每个子类中重写derivation()和toString()方法，在三角函数内设type属性存储三角函数类型。

然后，考虑到本次作业的特征，每项最多由幂函数*正弦函数*余弦函数的格式组成，故在Term类仅设置三个因子对象做为属性，并对无参数的构造方法初始化为系数为1，指数为0的形式，同时，为了将每项系数合为一起，我将幂函数的系数默认为项的系数，在每一项被加入到多项式时利用combineCoef()方法将三个函数的系数合并。

最后，将原来的Poly类内由存每项的系数和指数，改为存多个Term的容器，并且在addTerm()时利用isCoefZero()及时删去了零项。

总之，在对象的创建上，我整体实现了由factor→term→poly的层次结构。

关于求导方面，我利用三层结构的迭代求导，在Term类内的derivation()方法中根据f(x)*g(x)的求导规则进行特殊书写。

2、输入数据的格式判断及解析

对于Wrong Format!判断，我自定义了InputException()的例外，并在其中设置printError()方法，在检测到非法格式时抛出例外。在Main类中进行try-catch的捕捉。

由于上次作业我先对表达式进行处理，导致无法判断输入数据格式，在本次作业中，我将原来的PolyComputer类改为StringHandler类，进行输入数据的判断和处理，并在正则表达式中补入了空格，先根据正则表达式检测数据格式，然后用dispose()方法对表达式进行处理，最后以项为单位解析表达式，存入一个Poly对象中。

3、关于优化

这次的作业如果利用各种三角函数的公式，其实有很多点可以进行优化，但是很多时候实现并不容易，且容易引发很多未知bug，况且很多优化规则的实例出现概率很小，故我最后只在以下三个方面进行了优化。

sin²(x)+cos²(x)=1
同类项合并
x**2→x*x

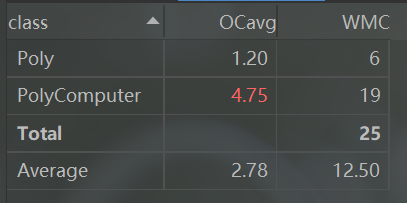
最后，我重构后的代码结构类图分析如下：

其中，StringHandler的循环复杂度较高，但因为涉及到字符串的解析，所以我认为是无法避免的。

优缺点评价

优点
- 结构层次较为清楚，有一定的可扩展性
- 各类功能简单，不易出现bug
- 实现了简单的优化
缺点
- 对Term类的属性处理不当，导致后面在增加多中因子时需要重构，改为存储Factor的容器
- 在Poly中进行优化时涉及到多个类的方法调用，耦合度较高
- 在StringHandler处理字符串时，生成项判断可以利用工厂方法来进行解耦，也会使思路更加清晰

bug分析

由于吸取了上一次的经验，之前进行了自我测试，并写了自动化测试工具进行测试，在强测及互测阶段，我的程序并没有被hack到，但我也知道它可能在某个神奇的地方仍存在bug

与此同时，在测试别人代码时，我偷懒使用了自动化测试工具，并且由于当时在忙一些其它的事情，我没有时间去分析完每个人的代码，自己构造的一些测试点也没有hack到别人，最后自动化测试也不争气，我体会了唯一一个和平的互刀环节。

第三次作业

作业要求

本次作业主要增加了三角函数的嵌套求导，并增加了表达式因子

实现简述

1、结构层次关系的设计

由于增加了表达式因子和嵌套的三角函数，我增加了NestFactor和ExprFunc两类，其中ExprFunc继承自Poly类，将原来的Factor父类改为存储变量因子的VariableFactor，并使所有的因子实现Factor接口，实现求导、加乘等一系列因子的基本操作。

在处理嵌套因子时，由于嵌套的求导规则是对每层进行求导并相乘，在这里，为了防止爆栈，我在NestFactor用了一个Factor的容器，从外向内存储嵌套每层因子，求导时只需对容器的每一项进行求导，对于三角函数括号内的部分在TriFunc中定义factor字符串直接进行存储，在输出时代替原来x的位置即可

具体的UML类图如下：

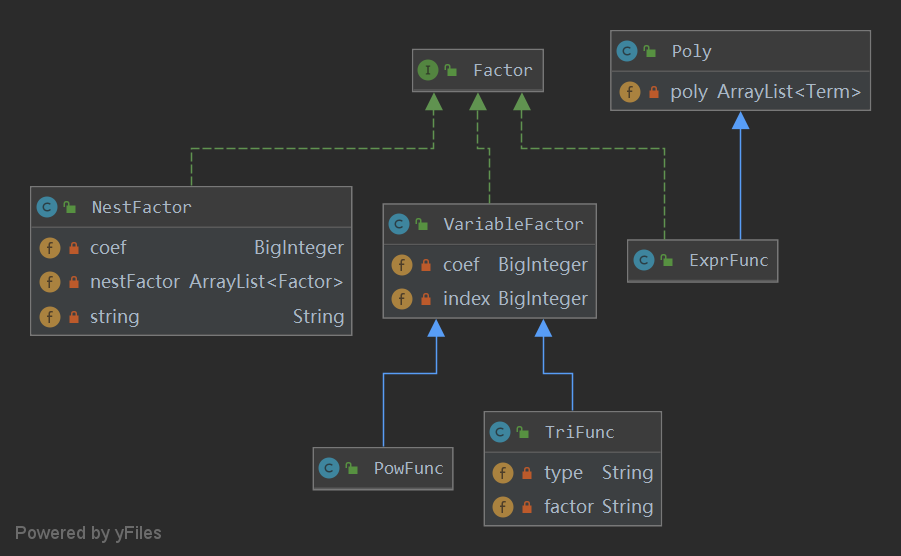
2、输入数据的格式判断及解析

在输入数据的格式判断，由于此次为含递归的正则表达式，不能简单用正则表达式直接判断，在此，我新建了一个FormatCheck类，对输入表达式进行递归判断，并专门写一个findRightBlacket()的静态方法，返回与当前字符串最左侧括号所匹配的右括号位置。

在解析表达式时，我新建了一个PolyHandler类，将表达式以项为单位传入Term中，循环填充一个Poly类的对象，同时，为了减少类之间的耦合度，我将格式检查也在这里进行。具体的关系如下图：

在解析表达式时，吸取上一次的经验，我新建了FactorFactory的工厂类，把解析出的因子表达式传入生成相应类型的Factor对象

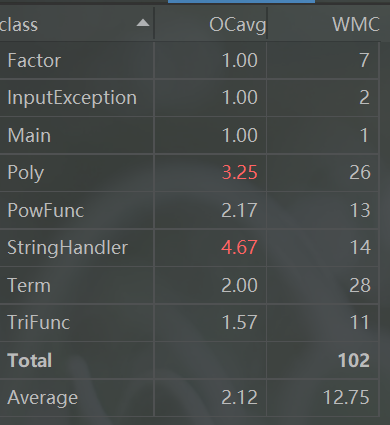
在下面类度量中，可以发现在，仍是在含表达式的解析的类循环复杂度比较高

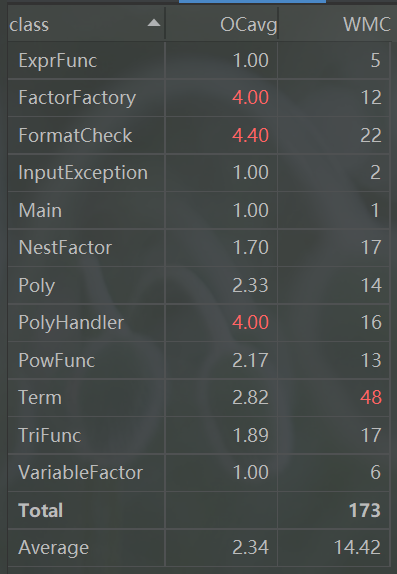
3、关于优化

实现了部分同类的因子和项之间的合并
在NestFactor中，通过重写的toString()对嵌套因子内部的字符串进行循环替换，简化了含前导0、符号多余以及因子之间可合并的地方
x**2→x*x

优缺点评价

优点
- 表达式的解析分为几部分在类的内部执行，减少了表达式解析的循环深度
- 迭代求导部分思路比较清楚
- 嵌套因子的处理较为简便
缺点
- 由于三角函数可被归为ExprFunc和TriFunc两类，同类项合并时不好判断
- 由于表达式因子的存在，使得因子求导的返回必须是Poly类对象，对于VariableFactor类，其实返回Factor类就够了，但还需要把他们一步步转成Poly类，觉得较为冗余，但也没有好的办法解决
- 在对求导结果进行复合时，需要分类处理，不能做到很好的归一化，否则会出现神奇的bug，感觉有点麻烦，应该还有解决办法

bug分析

这次作业太过复杂了，果然最后出现了一些很神奇的边缘bug，虽然很好改，但我被hack得很惨

在表达式因子求导得到Term类对象后，我将它toString()的结果传入了Term中进行新的一项的解析，但由于我将x**2转化成了x*x，会导致传入sin(x*x)类不合法因子，而我并未对此类因子进行解析，所以最终会出现RuntimeError
在由于优化，输出时可能会有sin(x*x)类不合法输出格式的因子
由于我在TriFunc类里的toString()方法内直接选择对factor为0的因子输出为0，导致有cos(0)时会出现错误

在测别人的bug时，我针对sin(0)**0，cos(0)等类型的易错点设置了测试样例，果然也hack到了一波别人，同时也测试了多层括号嵌套、连续符号判断等情况

总结

在这次作业中，我对面向对象的思想有了更深的理解，也更加意识到了层次化设计的重要性。一次重构的痛苦经历，也给了我足够的警醒，在以后的作业中，我会在一开始就考虑更具可扩展性的设计。