Counterfactual VQA: A Cause-Effect Look at Language Bias

目录

• 概
• 主要内容
  • 实现
• 代码

Niu Y., Tang K., Zhang H., Lu Z., Hua X. and Wen J. Counterfactual VQA: A Cause-Effect Look at Language Bias. CVPR, 2021.

概

利用因果分析消除VQA(Visual Question Answering (VQA))中的language bias.

主要内容

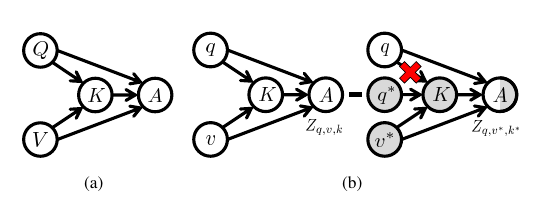
如上图所示,

\(Q\): question;

\(V\): image;

\(K\): multi-modal knowledge;

\(A\): answer.

影响最后决策\(A\)有三种:

1. \(Q \rightarrow A\), 直接受question影响, 比如模型对于所有的问图中的香蕉是什么颜色的问题均回答"黄色", 显然是不考虑图片的影响(因为可能是绿色), 这种实际上就是language bias;
2. \(V \rightarrow A\), 直接受图片影响;
3. \(V, Q \rightarrow K \rightarrow A\), 这里有一个mediator K, 即部分影响兼顾了\(Q, V\).

理想的VQA模型应该舍弃1中的影响, 在因果分析里头, 这部分direct effect被称之为natural direct effect (pure direct effect实际上):

\[NDE = A_{q, v^*, k*} - A_{q*, v^*, k^*}.
\]

余下的是TIE (total indirect effect):

\[TIE = TE - NDE = A_{q, v, k} - A_{q, v^*, k^*}.
\]

作者的思路是在inference的时候找到一个\(a\), 最大化TIE.

需要说明的是:

\[\mathrm{Pr}[A|do(Q, V, K)]
=\mathrm{Pr}[A|Q, V]\\
\mathrm{Pr}[A|do(Q, V^*, K^*)]
=\mathrm{Pr}[A|Q, V^*, K^*]\\
\]

这条件成立的原因单纯是因为作者的假设中并没有confounder, 实际上个人认为应当加一个\(V \rightarrow A\)的 arrow, 虽然这个并不影响上面的结论.

然后作者计算TIE也并不是针对\(A\), 而是\(A\)的score, \(Z=Z(Q=q, V=v, K=k)\).

实现

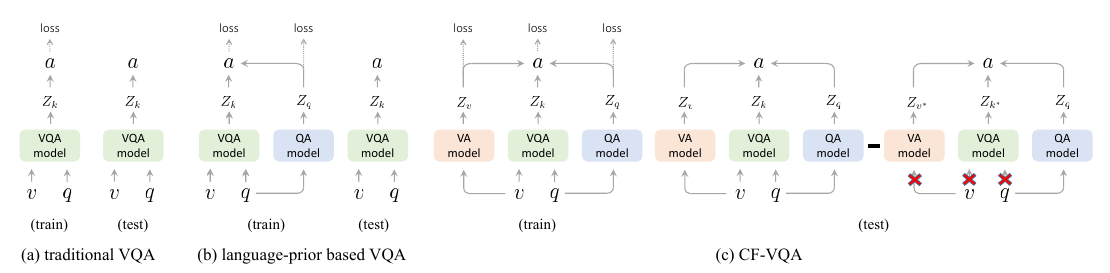
不同以往, 这一次可以显示地设置\(v^*, k^*\)了:

\[Z_q = \mathcal{F}_Q(q), Z_v=\mathcal{F}_V (v), Z_k=\mathcal{F}_{VQ}(v, q), Z_{q, v, k} = h(Z_q, Z_v, Z_k).
\]

特别的, 在\(q^*, v^*, k^*\)的情况下, 作者采取了如下的策略:

\[Z_q =
\left \{
\begin{array}{ll}
z_q = \mathcal{F}_Q(q), & \mathrm{if}\: Q= q \\
z_{q^*} = c, & \mathrm{if}\: Q=\empty.
\end{array}
\right .
\]

\[Z_v =
\left \{
\begin{array}{ll}
z_v = \mathcal{F}_V(v), & \mathrm{if}\: V= v \\
z_{v^*} = c, & \mathrm{if}\: V=\empty.
\end{array}
\right .
\]

\[Z_q =
\left \{
\begin{array}{ll}
z_k = \mathcal{F}_{VQ}(v,q), & \mathrm{if}\: V=v, Q = q \\
z_{k^*} = c, & \mathrm{if}\: V = \empty \: \mathrm{or}\: Q = \empty.
\end{array}
\right .
\]

这里\(c\)为可学习的变量.

注: 作者在代码中给出, \(c\)为一scalar, 也就是说实际上是:

\[z_* = c \cdot \mathbb{1}_{z}.
\]

作者也在文中指出, 这是为了一个Uniform的假设.

注: 看起来, 似乎应该对不同的\(Z_*\)指定不同的\(c\), 但是实际上, 是不影响的. 这一点是因为在下面HM和SUM的处理方式中, 无论是\(c_1\cdot c_2\cdot c_3\)

还是\(c_1 + c_2 + c_3\)都等价于\(c\) (这里要感谢作者的答复).

有了上面的准备, 下面是\(h\)的构造, 因为我们需要把不同的特征融合起来, 作者给出了两种方案:

1. Harmonic (HM):

\[h(Z_q, Z_v, Z_k) = \log \frac{Z_{HM}}{1 + Z_{HM}}, Z_{HM} = \sigma(Z_q) \cdot \sigma(Z_v) \cdot \sigma(Z_k).
\]

1. SUM:

\[h(Z_q, Z_v, Z_k) = \log \sigma(Z_{SUM}), Z_{SUM} = Z_q + Z_v + Z_k.
\]

在训练的时候, 用的是如下的损失:

\[\mathcal{L}_{cls} = \mathcal{L}_{VQA}(v, q, a)+ \mathcal{L}_{QA}(q, a) + \mathcal{L}_{VA}(v, a).
\]

以及, 为了训练\(c\)(且仅用于训练c),

\[\mathcal{L}_{kl} = \frac{1}{|A|}\sum_{a\in \mathcal{A}}-p(a|q,v,k)\log p(a|q, v^*,k^*),
\]

其中\(p(a|q,v,k)=softmax(Z_{q,v, k})\).

虽然感觉可以直接通过最大化TIE来训练c比较合理, 但是正如作者在附录中给出的解释一下, 这种情况明显会导致\(c \rightarrow 0\)并导致\(Z_{q, v^*, k^*}\rightarrow -\infty\).

代码

原文代码