noip提高组模拟赛(QBXT)T2

T2count题解

【 问题描述】:

小 A 是一名热衷于优化各种算法的 OIER,有一天他给了你一个随机生成的 1~n 的排列， 并定 义区间[l,r]的价值为：

\[\huge C_{l,r}=\max(a_i-a_j|l \le i,j \le r )
\]

他想请你告诉他， 所有区间的价值的总和为多少

【 输入】

第一行一个数 T(<=10)， 表示数据组数 对于每一组数据： 第一行一个数 n（ 1<=n,m<=100,000） 第二行 n 个数 a1...an， 表示一个 1~n 的随机的排列

【 输出】

对于每组数据输出一个数， 表示答案

【 输入样例】

1
4
3 2 4 1

【 输出样例】

14

【 数据范围】

对于 60%的数据： n<=1000

对于 100%的数据， n<=100,000

我们先看普通的暴力：

让\(mi[l][r]\)表示从\(l\)到\(r\)区间的最小值

让\(mx[l][r]\)表示从\(l\)到\(r\)区间的最大值

则答案为：

\[\large \sum_{l=1}^{n}\sum_{r=l}^{n}(mx[l][r]-mi[l][r])
\]

但是仔细观察式子我们可以发现：

\[\sum_{l=1}^{n}\sum_{r=l}^{n}(mx[l][r]-mi[l][r])=\sum_{l=1}^{n}\sum_{r=l}^{n}mx[l][r]-\sum_{l=1}^{n}\sum_{r=l}^{n}mi[l][r]
\]

然后mx和mi的部分我们可以单独求

所以以最大值为例子

一个点可以管辖的范围为左边第一个比他大的点到右边第一个比他大的点

我们设\(l[i]\)为左边第一个比\(a[i]\)大的位置\(r[i]\)为右边第一个比\(a[i]\)大的位置

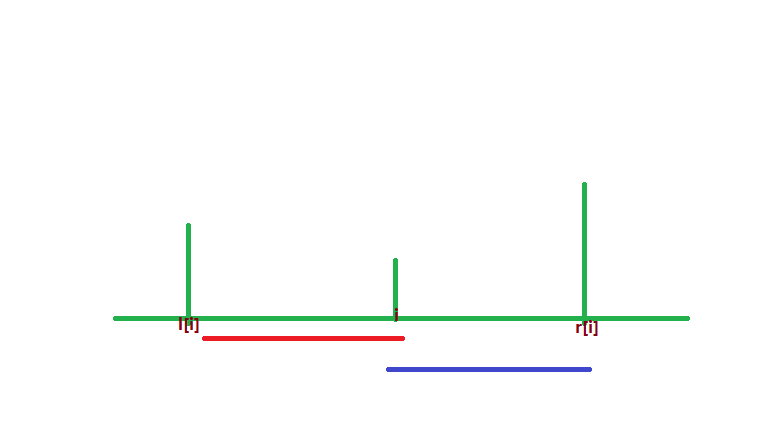
则只要满足\(l[i]<x\le i\)并且\(i\le y <r[i]\)的所有区间\([x,y]\)的最小大值都为i

所以这一部分区间我们把它乘起来

然后所有区间最大值的和为

\[\large \sum_{i=1}^{n}(r[i]-i)\times(i-l[i])\times a[i]
\]

最小值同理

然后求靠左/右的第一个比他大/小的数就可以用单调栈来解决

最后把最大值的和和最小值的和相减就是答案

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define int long long
#define clear(x) memset(x,0,sizeof x)
const int maxn=1e5+5;
int read(){
	int s=0,f=1;char ch;
	while(!isdigit(ch=getchar()))(ch=='-')&&(f=-1);
	for(s=ch-'0';isdigit(ch=getchar());s=s*10+ch-'0');
	return s*f;
}
int a[maxn];
int s1[maxn],t1;
int l[maxn],r[maxn];
int n;
int ans=0;
inline void clearlr(){for(int i=1;i<=n;++i){l[i]=0;r[i]=n+1;}}
signed main(){
#ifndef nFILE
	freopen("count.in","r",stdin);
	freopen("count.out","w",stdout);
#endif
	int T=read();
	while(T--){
		ans=0;
		n=read();
		clear(a);
		for(int i=1;i<=n;++i){(a[i]=read());}
		clear(s1);t1=0;
		clearlr();
		for(int i=1;i<=n;++i){
			while(t1&&a[s1[t1]]<a[i])r[s1[t1--]]=i;
			s1[++t1]=i;
		}
		clear(s1);t1=0;
		for(int i=n;i;--i){
			while(t1&&a[s1[t1]]<a[i])l[s1[t1--]]=i;
			s1[++t1]=i;
		}
		for(int i=1;i<=n;++i){ans+=(r[i]-i)*(i-l[i])*a[i];}
		clear(s1);t1=0;
		clearlr();
		for(int i=1;i<=n;++i){
			while(t1&&a[s1[t1]]>a[i])r[s1[t1--]]=i;
			s1[++t1]=i;
		}
		clear(s1);t1=0;
		for(int i=n;i;--i){
			while(t1&&a[s1[t1]]>a[i])l[s1[t1--]]=i;
			s1[++t1]=i;
		}
		for(int i=1;i<=n;++i){ans-=(r[i]-i)*(i-l[i])*a[i];}
		cout<<ans<<endl;
	}
	return 0;
}