BitArray编写埃拉托斯特尼筛法(原书错误,学习更正)
刚开始代码无法运行,修改后原书代码可以运行了,可是书本的思想还是错的。
虽然接下来的都是讲错误的思想下的“错误”的修改。
原书缺了窗体控件的代码,虽然在VS下不需要手动写窗体的代码,但是刚开始确实也不会怎么弄窗体
记录窗体拖拽的方法:
首要的一步是新建一个Windows窗体应用程序:文件 --> 新建 --> 项目 --> 选择Windows窗体应用程序;
此时VS界面左侧应当要有“工具箱”,有的话这里面的控件就可以直接拖了,没有的话需要设置
在第一排的菜单栏 -->点“重置窗口布局” -->左侧显示“工具箱” -->单击“工具箱” --> 选点击“公共控件” -->可拖拽各控件(Button/Label/ListBox/ListView/TextBox......)
书本窗体复原:
书本代码可运行版:
using System;
using System.Collections;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms; namespace WindowsFormsApplication3
{
public partial class Form1: Form
{
public Form1()
{
InitializeComponent();
} private void button1_Click(object sender, EventArgs e)
{
BitArray bitSet = new BitArray();
int value = Int32.Parse(txtValue.Text);
BuildSieve(bitSet);
// Console.WriteLine("bitSet.Get(value)" + bitSet.Get(value));
if(bitSet.Get(value))
lblPrime.Text = (value + "is a prime number." + bitSet.Get(value));
else
lblPrime.Text = (value + "is not a prime number." + bitSet.Get(value));
}
private void BuildSieve(BitArray bits)
{
string primes="";//这里要赋值,否则出错
for (int i = ; i <= bits.Count - ; i++)
bits.Set(i, true);
int lastBit = Int32.Parse(Convert.ToString(Math.Sqrt(bits.Count)));//注意:Int32.Parse(string);
for (int i = ; i <= lastBit - ; i++)
{
if (bits.Get(i))
for (int j = * i; j <= bits.Count - ; j++)
bits.Set(j, false);
int counter = ; for(int k=;k<=bits.Count-;k++)
{
if(bits.Get(k))
{
primes +=k.ToString();
counter++;
if((counter%)==)
primes+="\t";
else
primes+="\n";
}
}
txtPrimes.Text = primes; } } private void SeiveofEratosthenes_Load(object sender, EventArgs e)
{ }
}
}
但遗憾最后运行的结果与思想是不对的:
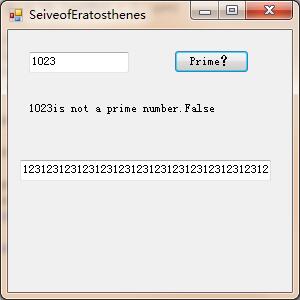
BitArray编写埃拉托斯特尼筛法(原书错误,学习更正)的更多相关文章
- LeetCode - 204. Count Primes - 埃拉托斯特尼筛法 95.12% - (C++) - Sieve of Eratosthenes
原题 原题链接 Description: Count the number of prime numbers less than a non-negative number, n. 计算小于非负数n的 ...
- 洛谷P3383 【模板】线性筛素数 (埃拉托斯特尼筛法)
题目描述 如题,给定一个范围N,你需要处理M个某数字是否为质数的询问(每个数字均在范围1-N内) 输入输出格式 输入格式: 第一行包含两个正整数N.M,分别表示查询的范围和查询的个数. 接下来M行每行 ...
- 统计所有小于非负整数 n 的质数的数量,埃拉托斯特尼筛法
素数的定义:质数又称素数.一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数. 1.暴力算法: 令i=2; 当i<n的时候,我们循环找出2-i的质数,即让i%(2~i-1), ...
- 周赛Problem 1021: 分蛋糕(埃拉托斯特尼筛法)
Problem 1021: 分蛋糕 Time Limits: 1000 MS Memory Limits: 65536 KB 64-bit interger IO format: %lld ...
- 利用OpenMP实现埃拉托斯特尼(Eratosthenes)素数筛法并行化 分类: 算法与数据结构 2015-05-09 12:24 157人阅读 评论(0) 收藏
1.算法简介 1.1筛法起源 筛法是一种简单检定素数的算法.据说是古希腊的埃拉托斯特尼(Eratosthenes,约公元前274-194年)发明的,又称埃拉托斯特尼筛法(sieve of Eratos ...
- LOJ6053 简单的函数 【Min_25筛】【埃拉托斯特尼筛】
先定义几个符号: []:若方括号内为一个值,则向下取整,否则为布尔判断 集合P:素数集合. 题目分析: 题目是一个积性函数.做法之一是洲阁筛,也可以采用Min_25筛. 对于一个可以进行Min_25筛 ...
- hdu 1431 素数回文(暴力打表,埃托色尼筛法)
这题开始想时,感觉给的范围5 <= a < b <= 100,000,000太大,开数组肯定爆内存,而且100000000也不敢循环,不超时你打我,反正我是不敢循环. 这题肯定得打表 ...
- 学习PHP爬虫--《Webbots、Spiders和Screen Scrapers:技术解析与应用实践(原书第2版)》
<Webbots.Spiders和Screen Scrapers:技术解析与应用实践(原书第2版)> 译者序 前言 第一部分 基础概念和技术 第1章 本书主要内容3 1.1 发现互联网的真 ...
- PHP和MySQL Web开发(原书第4版) 高清PDF+源代码
PHP和MySQL Web开发(原书第4版) 高清PDF+源代码 [日期:2014-08-06] 来源:Linux社区 作者:Linux [字体:大 中 小] 内容简介 <PHP和My ...
随机推荐
- 《面向对象的JavaScript》读书笔记
发现了2004年出版的一本好书,用两天快速刷了一遍,草草整理了一下笔记,在此备忘. 类:对象的设计蓝图或制作配方. 对象 === 实例 :老鹰是鸟类的一个实例 基于相同的类创建出许多不同的对象,类更多 ...
- JDK 中的监控与故障处理工具-04 (jmap)
jmap : memory map for java jmap 命令用于生成堆转储快照文件, 一般称为heapdump 或者 dump 文件.如果不是用 jmap 命令, 要获得 java 堆转储快照 ...
- Python学习札记(一) 初始python
参考: 廖雪峰教程:Python简介 笔记 1.C语言是可以用来编写操作系统的贴近硬件的语言,所以,C语言适合开发那些追求运行速度.充分发挥硬件性能的程序.而Python是用来编写应用程序的高级编程语 ...
- Hadoop 常用指令
1. 察看hdfs文件系统运行情况 bin/hdfs dfsadmin -report 2. 为了方便执行 HDFS 的操作指令,我们可以将需要的 Hadoop 路径写入环境变量中,便于直接执行命令. ...
- IO与NIO
IO IO概念: Java IO Java IO 即java的输入系统,不管我们编写任何种语言,都难免输入输出相关的媒介打交道,其实和媒介进行IO的过程是十分复杂的,还要考虑的因素特别多,比如我们要考 ...
- scp 上传 下载 文件
linux 中的ssh命令: scp 可以用来上传本地文件到远程服务器 或下载远程服务器中的文件到本地 1. 上传本地文件到远程服务器 scp readme.md user@www.*****.com ...
- mysql数据库优化课程---15、mysql优化步骤
mysql数据库优化课程---15.mysql优化步骤 一.总结 一句话总结:索引优化最立竿见影 1.mysql中最常用最立竿见影的优化是什么? 索引优化 索引优化,不然有多少行要扫描多少次,1亿行大 ...
- mysql 命令行参数说明
mysql --help -h : 主机名 -u : 用户名 -p : 密码 -P : 端口,不写默认(3306) -D :指定数据库(一般不指定) -e :查询语句 --column-names : ...
- Windows、Ubuntu双系统正确卸载Ubuntu系统
先判断启动方式,以管理员身份打开cmd或者power shell,输入bcdedit,找到path那一行,如果是winload.efi就是uefi引导,若为exe就是legacy引导 或者win+r输 ...
- 021——VUE中变异方法 push/unshift pop/shift
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
