Luogu P2680 运输计划(二分+树上差分)

P2680 运输计划

题意

题目背景

公元\(2044\)年,人类进入了宇宙纪元。

题目描述

公元\(2044\)年，人类进入了宇宙纪元。

\(L\)国有\(n\)个星球，还有\(n-1\)条双向航道，每条航道建立在两个星球之间，这\(n-1\)条航道连通了\(L\)国的所有星球。

小\(P\)掌管一家物流公司，该公司有很多个运输计划，每个运输计划形如：有一艘物流飞船需要从\(u_i\)号星球沿最快的宇航路径飞行到\(v_i\)号星球去。显然，飞船驶过一条航道是需要时间的，对于航道\(j\)，任意飞船驶过它所花费的时间为\(t_j\)，并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新，\(L\)国国王同意小\(P\)的物流公司参与\(L\)国的航道建设，即允许小\(P\)把某一条航道改造成虫洞，飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小\(P\)的物流公司就预接了\(m\)个运输计划。在虫洞建设完成后，这\(m\)个运输计划会同时开始，所有飞船一起出发。当这\(m\)个运输计划都完成时，小\(P\)的物流公司的阶段性工作就完成了。

如果小\(P\)可以自由选择将哪一条航道改造成虫洞，试求出小\(P\)的物流公司完成阶段性工作所需要的最短时间是多少？

输入输出格式

输入格式：

第一行包括两个正整数\(n, m\)，表示\(L\)国中星球的数量及小\(P\)公司预接的运输计划的数量，星球从\(1\)到\(n\)编号。

接下来\(n-1\)行描述航道的建设情况，其中第\(i\)行包含三个整数\(a_i,b_i\)和\(t_i\)，表示第\(i\)条双向航道修建在\(a_i\)与\(b_i\)两个星球之间，任意飞船驶过它所花费的时间为\(t_i\)。数据保证\(1 \leq a_i,b_i \leq n\)且\(0 \leq t_i \leq 1000\)。

接下来\(m\)行描述运输计划的情况，其中第\(j\)行包含两个正整数\(u_j\)和\(v_j\)，表示第\(j\)个运输计划是从\(u_j\)号星球飞往\(v_j\)号星球。数据保证\(1 \leq u_i,v_i \leq n\)。

输出格式：

一个整数，表示小\(P\)的物流公司完成阶段性工作所需要的最短时间。

输入输出样例

输入样例：

6 3
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5

输出样例：

11

说明

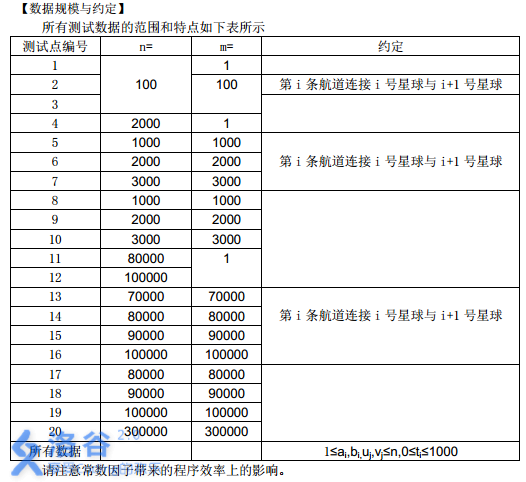
所有测试数据的范围和特点如下表所示

思路

树上差分板子题，要不你试试？ --logeadd

过了一个月终于把它试出来了...

首先对于答案我们来二分，二分的左区间为\(0\)（当然，最优的左区间并不是\(0\)），有区间为最长的运输计划的长度。

运输区间的长度可以用\(O( \log ^2 n)\)的树链剖分或者\(O( \log n)\)的倍增算法（按照这题的数据强度的话后者显然更可过），可是我们如何判定二分出的答案是否可行呢？

首先处理出长度超过二分答案的边的数量\(sum\)，然后从根跑一边\(dfs\)，统计每个结点下的每一子树中有多少点在计划中会走到该子树的根结点。如果该值为\(sum\)，则用这条边更新最大边权，最后直接看最长计划长度减去最大边权是否小于二分答案即可。

现在又有问题了：如何快速统计呢?这就需要树上差分了。对于每一个计划我们把它看成两个部分：从\(u\)到\(LCA(u,v)\)和从\(LCA(u,v)\)到\(v\)，我们再不妨把所有分出的部分都看成向上运输的计划，即把它看成这样的两部分：从\(u\)到\(LCA(u,v)\)和从\(v\)到\(LCA(u,v)\)。然后在树上统计每一结点作为计划开头的次数，记为正数；统计每一结点作为结尾的次数，记为负数。

那么按照上面\(dfs\)的思路，我们就可以这么写：

int dfs2(int now)//先看下面那个函数
{
    int re=0;//该结点信息
    for(register int i=top[now];i;i=nex[i])
    {
        if(to[i]==fa[now][0]) continue;
        int lzq=dfs2(to[i]);//该结点下的子树信息，
        re+=lzq;
        if(lzq==sum&&len[i]>tmp) tmp=len[i];//如果刚好有sum条边，更新答案
    }
    return re+js[now];
}
inline bool check(int now)//二分出的答案为now
{
    memset(js,0,sizeof js);//结点作为计划开头的次数计数
    tmp=-0x3f3f3f3f,sum=0;//sum记录需要减少时间的计划数量，tmp记录有sum条边同时经过的边的最大长度
    for(register int i=0;i<m;i++) if(tim[i]>now) sum++,js[u[i]]++,js[v[i]]++,js[st[i]]-=2;//计数统计
    dfs2(1);//开始dfs
    return max_time-tmp<=now;//判断最大时间的一个计划的时间是否可减少至now
}

AC代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN=3e5+5;
int n,m,u[MAXN],v[MAXN],st[MAXN],tim[MAXN];
int cnt,top[MAXN],to[MAXN<<1],len[MAXN<<1],nex[MAXN<<1];
int dep[MAXN],dis[MAXN],fa[MAXN][20];
int L,R,ans,max_time,tmp,sum,js[MAXN];
inline int read()
{
    int re=0;
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
void dfs1(int now)
{
    for(register int i=1;i<=19;i++) fa[now][i]=fa[fa[now][i-1]][i-1];
    for(register int i=top[now];i;i=nex[i])
    {
        if(to[i]==fa[now][0]) continue;
        dis[to[i]]=dis[now]+len[i],dep[to[i]]=dep[now]+1,fa[to[i]][0]=now;
        dfs1(to[i]);
    }
}
int dfs2(int now)
{
    int re=0;
    for(register int i=top[now];i;i=nex[i])
    {
        if(to[i]==fa[now][0]) continue;
        int lzq=dfs2(to[i]);
        re+=lzq;
        if(lzq==sum&&len[i]>tmp) tmp=len[i];
    }
    return re+js[now];
}
inline int LCA(int x,int y)
{
    if(dep[x]<dep[y]) swap(x,y);
    for(register int i=19;i>=0;i--) if(dep[fa[x][i]]>=dep[y]) x=fa[x][i];
    if(x==y) return x;
    for(register int i=19;i>=0;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}
inline bool check(int now)
{
    memset(js,0,sizeof js);
    tmp=-0x3f3f3f3f,sum=0;
    for(register int i=0;i<m;i++) if(tim[i]>now) sum++,js[u[i]]++,js[v[i]]++,js[st[i]]-=2;
    dfs2(1);
    return max_time-tmp<=now;
}
int main()
{
    n=read(),m=read();
    for(register int i=0;i<n-1;i++)
    {
        int x=read(),y=read(),z=read();
        to[++cnt]=y,len[cnt]=z,nex[cnt]=top[x],top[x]=cnt;
        to[++cnt]=x,len[cnt]=z,nex[cnt]=top[y],top[y]=cnt;
    }
    dep[1]=1;
    dfs1(1);
    for(register int i=0;i<m;i++)
    {
        u[i]=read(),v[i]=read(),st[i]=LCA(u[i],v[i]);
        tim[i]=dis[u[i]]-dis[st[i]]+dis[v[i]]-dis[st[i]];
        if(tim[i]>max_time) max_time=tim[i];
    }
    L=0,R=max_time;
    while(L<=R)
    {
        int mid=(L+R)>>1;
        if(check(mid)) ans=mid,R=mid-1;
        else L=mid+1;
    }
    printf("%d",ans);
    return 0;
}