Educational Codeforces Round 80 (Rated for Div. 2)(A-E)

C D E 这三道题感觉挺好

 

 

 

决定程序是否能通过优化在要求的时间内完成，程序运行时间为t，你可以选择花X天来优化，优化后程序的运行时间为t/(x+1)取上整，花费的时间为程序运行时间加上优化时间

如果程序运行时间小于等于要求时间，那就不需要优化，否则必须优化，假设优化X天，那么总时间就是X+t/(X+1) ,我们的目标事求他的最小值，根据均值不等式

另外均值不等式中等于号成立的条件是x1=x2=....xn

code

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1e4+5;
int main(){
	int T;
	scanf("%d",&T);
	while(T--){
		int n,d;
		scanf("%d%d",&n,&d);
		if(d<=n) puts("YES");
		else {
			int x=sqrt(d);
			int ans=min(ceil(1.0*d/x)+x,ceil(1.0*d/(x+1))+(x+1));
			if(ans<=n+1) puts("YES");
			else puts("NO");
		}
	} 

}
 

　

对式子进行化简即可发现规律 ，偷懒直接贴官方的题解

#include<cstdio>
#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
int main(){
	int T;
	cin>>T;
	while(T--){
		int a,b;
		cin>>a>>b;
		ll now=9,cnt=0;
		while(now<=b){
			now=now*10+9;
			cnt++;
		}
		cout<<1ll*a*cnt<<endl;
	}
}
 

　　

两种方法，都需要发现一个性质就是一个长度为2*m的非递减序列仅能构造出一个解

所以这道题本质上是找到使用1-n能凑出多少个不同的非递减序列，并且不能重复

法一： 

法二：问题等价于1-n中每一个数有无限个，从中挑出2*m个元素组成一个集合，有多少种选法，答案是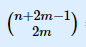

#include<cstdio>
#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
const ll P=1e9+7;
ll jc[1100],inv[1100];
ll qpow(ll a,int n){
	ll ans=1;
	for(;n;n>>=1,a=a*a%P)
		if(n&1) ans=ans*a%P;
	return ans;
}
int main(){
	jc[0]=1;
	for(int i=1;i<=1050;i++){
		jc[i]=jc[i-1]*i%P;
		inv[i]=qpow(jc[i],P-2);
	}
	inv[0]=1;
	int n,m;
	cin>>n>>m;
	cout<<jc[n+2*m-1]*inv[2*m]%P*inv[n-1]%P<<endl;
}
 

　　

先贴一波官方题解

先二分答案，然后将矩阵的每一行压缩成一个m位的二进制 数（如果比X小就赋值为0，否则赋值为1）这样问题就转化为了是否存在两个数异或值为2^m-1

由于n比较大，不能n^2，但是发现可能的二进制数很少，所以我们可以用将可能的二进制数存下来，然后去枚举这些二进制数，复杂度不高了

#include<cstdio>
#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
const int dim1=3e5+5;
const int dim2=8;
int a[dim1][dim2];
int n,m;
int ans_l,ans_r;
bool check(int x){
	vector<int> mask(1<<m,-1);
	for(int i=0;i<n;i++){
		int now=0;
		for(int j=0;j<m;j++){
			if(a[i][j]>=x) now^=1<<j;
		}
		mask[now]=i;
	}
	for(int m1=0;m1<1<<m;m1++){
		for(int m2=0;m2<1<<m;m2++){
			if(mask[m1]!=-1 && mask[m2]!=-1 && (m1|m2)==(1<<m)-1) {
				ans_l=mask[m1],ans_r=mask[m2];
				return 1;
			}
		}
	}
	return false;
}
int main(){
	cin>>n>>m;
	for(int i=0;i<n;i++)
		for(int j=0;j<m;j++)
			scanf("%d",&a[i][j]);
	int l=1,r=1e9;
	while(l<r){
		int mid=(l+r+1)/2;
		if(check(mid)) l=mid;
		else r=mid-1;
	}
	check(l);
	printf("%d %d\n",ans_l+1,ans_r+1);

}
 

　　

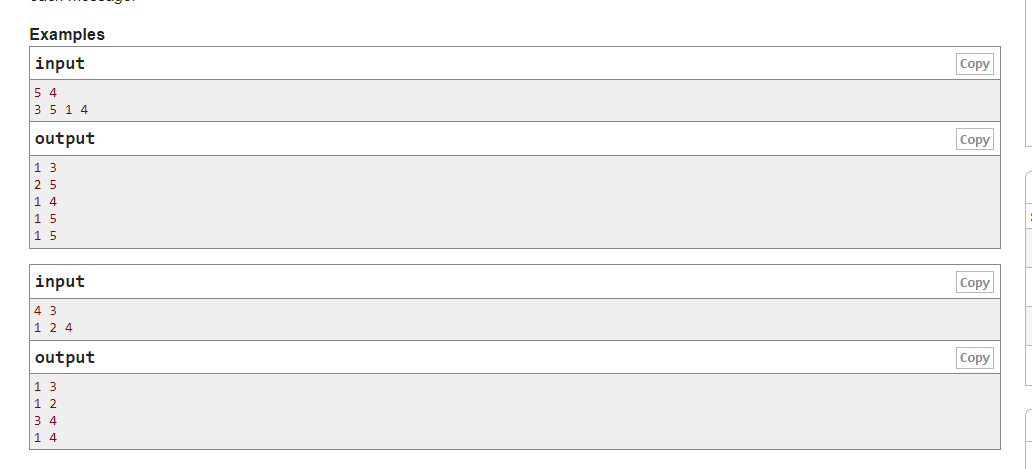
法一 好想但是代码比较复杂

最小值很容易确定，出现过就是1，否则就是其初始位置

对于每一个数来说，他的最大值有两种情况，第一种是他第一次到达队首之前的位置是哪里，这个等价于计数他前面有多少个数比他大，树状数组来解决

第二个就是相邻两次到达队首的时刻，这个就是就是计数两次之间有多少个不同的数，这个用莫队来完成

法二：模拟移动过程，但是需要将队列逆序，这样避免的移动，插入队首的操作可以看做是队尾增加一个数

插入的同时计算并更新最大值

说的比较粗略，具体看官方题解

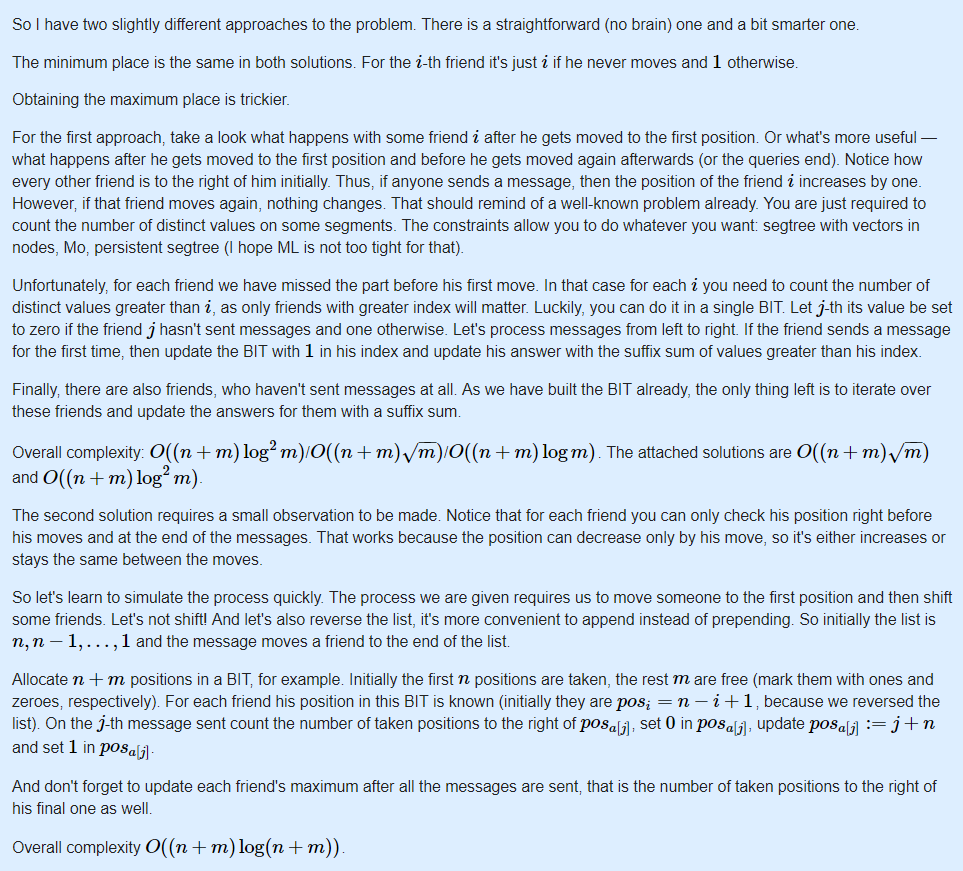
法一 树状数组+莫队

#include<bits/stdc++.h>

#define X first
#define Y second 

using namespace std;

const int N=3e5+5;
const int tk=550;

typedef pair<int,int> pi;
typedef long long ll;

int cnt[N],tot;

vector<int> pos[N];

int a[N];

void add(int x){
	++cnt[x];
	if (cnt[x] == 1) ++tot;
}

void rem(int x){
	if (cnt[x] == 1) --tot;
	--cnt[x];
}

int f[N];

void upd(int x){
	for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
		++f[i];
}

int get(int x){
	int res = 0;
	for (int i = x; i < N; i |= i + 1)
		res += f[i];
	return res;
}

int main(){
	int n,m;
	cin>>n>>m;
	for(int i=0;i<m;i++){
		scanf("%d",&a[i]);
		--a[i];
	}
	for(int i=0;i<m;i++){
		pos[a[i]].push_back(i);
	}
	vector<pi> qr;
	for(int i=0;i<n;i++){
		for(int j=1;j<pos[i].size();j++){
			qr.push_back(make_pair(pos[i][j-1]+1,pos[i][j]-1));
		}
		if(!pos[i].empty()) qr.push_back(make_pair(pos[i].back()+1,m-1));
	}

	sort(qr.begin(),qr.end(),[](pi x,pi y){
		if(x.X/tk!=y.X/tk) return x.X<y.X;
		if((x.X/tk)&1) return x.Y<y.Y;
		return x.Y>y.Y;
	});
	vector<pi> ans(n);
	for(int i=0;i<n;i++)
		ans[i]={i,i};
	for(int i=0;i<m;i++)
		ans[a[i]].X=0;
	int L=0,R=-1;
	for(int i=0;i<(int)qr.size();i++){
		int l=qr[i].X,r=qr[i].Y;
		if(l>r) continue;
		int x=a[qr[i].X-1];
		while(L<l) rem(a[L++]);
		while(L>l) add(a[--L]);
		while(R>r) rem(a[R--]);
		while(R<r) add(a[++R]);
		ans[x].Y=max(ans[x].Y,tot);
	}
	for(int i=0;i<m;i++){
		if(i==pos[a[i]][0]) {
			ans[a[i]].Y=max(ans[a[i]].Y,a[i]+get(a[i]));
			upd(a[i]);
		}
	}
	for(int i=0;i<n;i++){
		if(pos[i].empty()){
			ans[i].Y=max(ans[i].Y,i+get(i));
		}
	}
	for(int i=0;i<n;i++){
		printf("%d %d\n",ans[i].X+1,ans[i].Y+1);
	}
}

法2 树状数组

#include<bits/stdc++.h>

using namespace std;

const int maxn=6e5+5;

int f[maxn];

void upd(int x,int val){
	for(int i=x;i>=0;i=(i&(i+1))-1)
		f[i]+=val;
}

int get(int x){
	int res=0;
	for(int i=x;i<maxn;i|=i+1)
		res+=f[i];
	return res;
}

int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	vector<int> mi(n);
	iota(mi.begin(),mi.end(),0);
	vector<int> mx=mi;
	vector<int> a(m);
	for(int i=0;i<m;i++)
		scanf("%d",&a[i]),--a[i],mi[a[i]]=0;
	vector<int> pos(n);
	for(int i=0;i<n;i++)
		pos[i]=n-i-1;
	for(int i=0;i<n;i++)
		upd(i,1);
	for(int i=0;i<m;i++){
		mx[a[i]]=max(mx[a[i]],get(pos[a[i]]+1));
		upd(pos[a[i]],-1);
		pos[a[i]]=i+n;
		upd(pos[a[i]],1);
	}
	for(int i=0;i<n;i++)
		mx[i]=max(mx[i],get(pos[i]+1));
	for(int i=0;i<n;i++)
		printf("%d %d\n",mi[i]+1,mx[i]+1);
	return 0;
}