求两个有序数组的中位数或者第k小元素

问题：两个已经排好序的数组，找出两个数组合并后的中位数（如果两个数组的元素数目是偶数，返回上中位数）。

设两个数组分别是vec1和vec2，元素数目分别是n1、n2。

算法1：最简单的办法就是把两个数组合并、排序，然后返回中位数即可，由于两个数组原本是有序的，因此可以用归并排序中的merge步骤合并两个数组。由于我们只需要返回中位数，因此并不需要真的合并两个数组，只需要模拟合并两个数组：每次选数组中较小的数，统计到第（n1+n2+1）/2个元素就是要找的中位数。算法复杂度为O(n1+n2)

int findMedian_merge(vector<int> &vec1, vector<int> &vec2)
{
    int N1 = vec1.size(), N2 = vec2.size();
    int medean = (N1 + N2 + 1) / 2, i = 0, j = 0;
    for(int k = 1; k < medean; k++)
    {
        if(i < N1 && j < N2)
        {
            if(vec1[i] < vec2[j])i++;
            else j++;
        }
        else if(i >= N1)//数组vec1到达末尾
            j++;
        else if(j >= N2)//数组vec2到达末尾
            i++;
    }
    if(i < N1 && j < N2)
        return vec1[i] < vec2[j] ? vec1[i] : vec2[j];
    else if(i >= N1)
        return vec2[j];
    else if(j >= N2)
        return vec1[i];
}

讲下面的算法之前，先说2个结论1：某个数组中有一半的元素不超过数组的中位数，有一半的元素不小于中位数（如果数组中元素个数是偶数，那么这里的一半并不是严格意义的1/2）。结论2：如果我们去掉数组比中位数小的k个数，再去掉比中位数大的k个数，得到的子数组的中位数和原来的中位数相同。

算法2：利用折半查找的思想，假设两个数组的中位数分别是vec1[m1], vec2[m2]                                                      本文地址

1、如果vec1[m1] = vec2[m2] ，那么刚好有一半元素不超过vec1[m1]，则vec1[m1]就是要找的中位数。

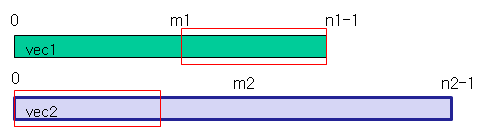
2、如果vec1[m1] < vec2[m2] 根据结论1很容易可以推理出，这个中位数只可能出现在vec1[n1/2,…,n1-1]或vec2[0,…,(n2-1)/2]中，那么vec1[n1/2,…,n1-1]和vec2[0,…,(n2-1)/2]的中位数是不是和原来两个数组的中位数相同呢？根据结论2，如果原数组长度相等，即n1=n2，那么中位数不变；如果长度不相等，vec2中去掉的大于中位数的数的个数 > vec1中去掉的小于中位数的数的个数 ，则中位数不一定不变。因此我们要在两个数组中去掉相同个数的元素。如下图所示，假设n1 < n2, 两个数组都去掉n1/2个元素，则子数组vec1[n1/2,…,n1-1]和vec2[0,…,n2-1-n1/2]的中位数和原来的中位数相同，图中红色方框里是去掉的元素。

注意：在n1<n2的假设下，不管我们是求上中位数还是下中位数，我们每次去掉的元素都是n1/2（整数除法）个。例如vec1 = [1,3,5,7],vec2 = [2,4,6,8], 如果我们要求的是上中位数，m1 = m2 =1，即3 < 4, 要删掉vec1的前半段，这里vec1[m1] = 3 要不要删除呢，我们只要判断一下3能否可能成为中位数，假设3是中位数，不超过3的数只有3个（1,2,3），总得元素有8个，因此3不可能成为上中位数，我们可以在vec1中删除2两个元素。如果是求下中位数，即m1 = m2 = 2，即5 < 6,删除vec1前半段时要不要删除5呢？注意到比不超过5的数有5个，不低于5的数有4个，因此5有可能成为下中位数，因此5不能删除，vec1中只能删除左边两个元素。同理当vec1的个数是奇数时，vec1的中位数永远不能删除，即只能删除vec1的n1/2（整数除法）个元素

3、如果vec1[m1] > vec2[m2] ，同上分析，中位数只可能出现在vec1的前半段或vec2的后半段。如下图所示，两个数组分别去掉n1/2个元素后，子数组vec1[0,…,n1/2-1]和vec2[n1/2,…,n2-1]的中位数和原来的中位数相同

子数组递归求解，即可求出中位数，算法复杂度为O(log(n1+n2)).注意一下递归结束条件和边界处理。如果要求下中位数只要稍作修改，可以参考另一篇博客

int findMedian_logn(int vec1[], int n1, int vec2[], int n2)
{
    int m1 = (n1-1) / 2, m2 = (n2-1) / 2;
    if(n1 == 1)
    {//递归结束条件
        if(n2 == 1)
            return vec1[0] < vec2[0] ? vec1[0] : vec2[0];
        if(n2 % 2 == 0)
        {
            if(vec1[0] >= vec2[m2+1])
                return vec2[m2+1];
            else if(vec1[0] <= vec2[m2])
                return vec2[m2];
            else return vec1[0];
        }
        else
        {
            if(vec1[0] >= vec2[m2])
                return vec2[m2];
            else if(vec1[0] <= vec2[m2-1])
                return vec2[m2-1];
            else return vec1[0];
        }
    }
    else if(n2 == 1)
    {//递归结束条件
        if(n1 % 2 == 0)
        {
            if(vec2[0] >= vec1[m1+1])
                return vec1[m1+1];
            else if(vec2[0] <= vec1[m1])
                return vec1[m1];
            else return vec2[0];
        }
        else
        {
            if(vec2[0] >= vec1[m1])
                return vec1[m1];
            else if(vec2[0] <= vec1[m1-1])
                return vec1[m1-1];
            else return vec2[0];
        }
    }
    else
    {
        int cutLen = n1/2 > n2/2 ? n2/2 : n1/2;//注意每次减去短数组的一半，如果数组长度n是奇数，一半是指n-1/2
        if(vec1[m1] == vec2[m2])return vec1[m1];
        else if(vec1[m1] < vec2[m2])
            return findMedian_logn(&vec1[cutLen], n1-cutLen, vec2, n2-cutLen);
        else
            return findMedian_logn(vec1, n1-cutLen, &vec2[cutLen], n2-cutLen);
    }
}

算法3：这里我们把问题扩展一下，求两个有序数组的第k小的元素。我们假设这个第k小的元素是X，若X在数组vec1的第i个位置，如果把X放到vec2中，那么X在排数组vec2中的第（k-i+1）个位置，则X >= vec2中第k-i个元素 且 X <= vec2中第k-i+1个元素。

因此我们可以首先假设元素X在数组vec1中，对vec1中的元素进二分查找。

选取vec1中的元素vec1[idx1]（idx1 = n1/(n1+n2)*(k-1), 即第idx1+1个元素，由于不是中位数，因此不是选取中间元素），看vec2中的元素vec2[idx2]（idx2 = k-idx1-2, 即第k-idx1-1个元素）：

注意到这里的一个不变式：idx1及前面元素的个数 + idx2及前面元素的个数 = k，即（idx1+1）+（idx2+1）= k

1、如果vec1[idx1] == vec2[idx2] ,刚好有idx1+1+idx2+1 = k个元素不超过vec1[idx1], 则vec1[idx1]为所求

2、如果vec1[idx1] < vec2[idx2], 不超过vec1[idx1]的元素个数肯定小于k，因此vec1[idx1]以及其前面的元素肯定小于我们要求的元素；对于vec2[idx2+1]以及其后面的元素，不超过他们的数的个数肯定大于K个，因此vec2[idx2+1]以及其后面的元素肯定大于我们要求的元素。故搜索范围缩小到vec1[idx1+1,…,n1-1] 和vec2[0...idx2]

3、如果vec1[idx1] > vec2[idx2], 同理搜索范围缩小到vec1[0...idx1]和vec2[idx2+1,....n2-1]

其实算法思想和上面的算法2相同。上述算法也可以每次取vec1和vec2的第k/2个元素比较，这样每次可以使k减小一半，可以参考here

注意边界处理。算法中每次迭代平均k都会减小约k/2,因此算法复杂度为O（logk），而k = （n1+n2）/m, m是一个常数，即复杂度为O（log(n1+n2)）

 //找到两个有序数组中第k小的数,k>=1
     int findKthSmallest(int vec1[], int n1, int vec2[], int n2, int k)
     {
         //边界条件处理
         if(n1 == )return vec2[k-];
         else if(n2 == )return vec1[k-];
         if(k == )return vec1[] < vec2[] ? vec1[] : vec2[];

         int idx1 = n1*1.0 / (n1 + n2) * (k - );
         int idx2 = k - idx1 - ;

         if(vec1[idx1] == vec2[idx2])
             return vec1[idx1];
         else if(vec1[idx1] < vec2[idx2])
             return findKthSmallest(&vec1[idx1+], n1-idx1-, vec2, idx2+, k-idx1-);
         else
             return findKthSmallest(vec1, idx1+, &vec2[idx2+], n2-idx2-, k-idx2-);
     }

算法4：对于寻找两个有序数组第k小的元素，还有一种简化算法1，复杂度为O（k）的算法，在归并两个数组的过程中，如果如果已经选择的元素达到k，就不许要再归并下去了。

参考资料：

kenby：http://blog.csdn.net/kenby/article/details/6833407

David Luo：http://www.cnblogs.com/davidluo/articles/k-smallest-element-of-two-sorted-array.html

Hackbuteer1: http://blog.csdn.net/hackbuteer1/article/details/7584838

Median of Two Sorted Arrays

Find the k-th Smallest Element in the Union of Two Sorted Arrays

 leetcode之 median of two sorted arrays

【版权声明】转载请注明出处：http://www.cnblogs.com/TenosDoIt/p/3554479.html