支持向量机-SVM 学习
一 、支持向量机(SVM)
1.1 符号定义
标签 y 不再取 0 或 1,而是: y∈{-1, 1}
定义函数:
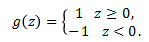
向量,没有第 0 个维度,b 为截距,预测函数定义为:

1.2 函数间隔与几何间隔
1.2.1 函数间隔
样本个体:

全体:

1.2.2 几何间隔
样本个体:

全体:
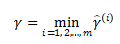
1.2.3 关系
函数间隔与几何间隔都是对预测置信度的度量,这个间隔越大,说明预测样本离着分界线越远,我们预测的结果也就更加可靠。

1.3 优化目标
假设样本是线性可分的,优化目标为
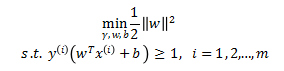
1.4 广义拉格朗日乘数法
带约束的优化为:
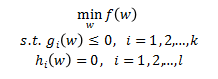
转化为:
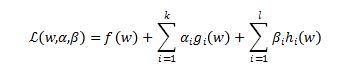
【原始问题】:
记量 为:
为: 
原始问题为:
【对偶问题】:
记量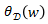 为:
为: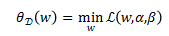
对偶问题为: 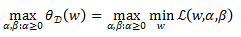
对于原始问题和对偶问题,以下关系恒成立:
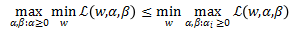
KKT条件:

当KKT条件满足时,对偶问题和原始问题有着相同的解。
1.5 最优间隔分类器
SVM的拉格朗日乘数法:
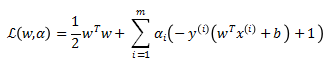
原始问题:
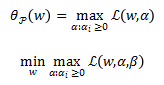
对偶问题:

根据KKT条件:
对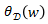 关于
关于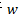 求梯度,令之为0,可得:
求梯度,令之为0,可得:
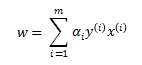
对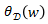 关于 b 求导,令之为0,可得:
关于 b 求导,令之为0,可得:
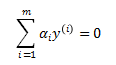
带回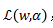 ,得:
,得:

因此SVM的对偶问题为:

将对偶解 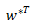 带入原始问题,对所有的
带入原始问题,对所有的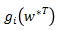 不等于 0 对应的系数
不等于 0 对应的系数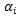 求导,令其等于0,得:
求导,令其等于0,得:

因为 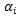 不为的项
不为的项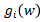 为0,即该点为支持向量。理想情况分割线两侧各有一个最近的点,且我们也仅在两侧各取一个点。因此,对于
为0,即该点为支持向量。理想情况分割线两侧各有一个最近的点,且我们也仅在两侧各取一个点。因此,对于 的,两侧同时乘 -1,累加两个式子得:
的,两侧同时乘 -1,累加两个式子得:
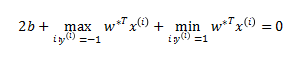
即:

上述算法称为最优间隔分类器。
1.6 SVM核
将 中的内积
中的内积 替换为
替换为 ,称
,称 为核。核 K 的合法取法有很多,如:
为核。核 K 的合法取法有很多,如:
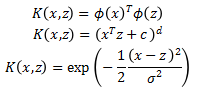
不同的核将 x 和 z 映射到了不同的空间之中,一组低维的向量投射至高维通常更容易划分。
1.7  正则化与软间隔
正则化与软间隔
对于一些线性不可分的情况,或者为了抵制噪音的影响,使用 软边距进行处理。为每组数据加入一个允许误差
软边距进行处理。为每组数据加入一个允许误差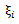 ,同时在优化目标中加入惩罚项
,同时在优化目标中加入惩罚项 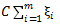 。SVM的原始优化问题变为:
。SVM的原始优化问题变为:
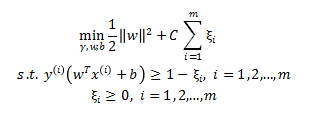
拉格朗日乘数法写作:
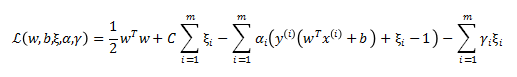
根据KKT条件,
令 ,得:
,得: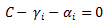
令 ,得:
,得:
令 ,得:
,得:
同样求对偶问题得到:

根据KKT条件,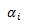 取值的关系如下:
取值的关系如下:
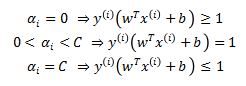
注意,b 不再是原始SVM的取值。
【Reference】
1. 支持向量机通俗导论(理解SVM的三层境界) 【这篇写的非常好】
支持向量机-SVM 学习的更多相关文章
- OpenCV 学习笔记 07 支持向量机SVM(flag)
1 SVM 基本概念 本章节主要从文字层面来概括性理解 SVM. 支持向量机(support vector machine,简SVM)是二类分类模型. 在机器学习中,它在分类与回归分析中分析数据的监督 ...
- 支持向量机通俗导论(SVM学习)
1.了解SVM 支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是 ...
- 转:SVM与SVR支持向量机原理学习与思考(一)
SVM与SVR支持向量机原理学习与思考(一) 转:http://tonysh-thu.blogspot.com/2009/07/svmsvr.html 弱弱的看了看老掉牙的支持向量机(Support ...
- coursera机器学习-支持向量机SVM
#对coursera上Andrew Ng老师开的机器学习课程的笔记和心得: #注:此笔记是我自己认为本节课里比较重要.难理解或容易忘记的内容并做了些补充,并非是课堂详细笔记和要点: #标记为<补 ...
- Stanford机器学习---第八讲. 支持向量机SVM
原文: http://blog.csdn.net/abcjennifer/article/details/7849812 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回 ...
- SVM学习笔记
一.SVM概述 支持向量机(support vector machine)是一系列的监督学习算法,能用于分类.回归分析.原本的SVM是个二分类算法,通过引入“OVO”或者“OVR”可以扩展到多分类问题 ...
- 【IUML】支持向量机SVM
从1995年Vapnik等人提出一种机器学习的新方法支持向量机(SVM)之后,支持向量机成为继人工神经网络之后又一研究热点,国内外研究都很多.支持向量机方法是建立在统计学习理论的VC维理论和结构风险最 ...
- [转]支持向量机SVM总结
首先,对于支持向量机(SVM)的简单总结: 1. Maximum Margin Classifier 2. Lagrange Duality 3. Support Vector 4. Kernel 5 ...
- 机器学习:Python中如何使用支持向量机(SVM)算法
(简单介绍一下支持向量机,详细介绍尤其是算法过程可以查阅其他资) 在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别.分类(异 ...
随机推荐
- VB.NET,C#.NET调用Web Service,利用visual studio 的实现方法
下面是一篇文章比较详细,其实具体操作很简单,把Web Service服务地址,利用工具(VS2010),通过添加引用的形式,添加到项目中来就可以应用了. 大家如果这个地方不会操场的话,可以问问我QQ: ...
- tf.contrib.rnn.static_rnn与tf.nn.dynamic_rnn区别
tf.contrib.rnn.static_rnn与tf.nn.dynamic_rnn区别 https://blog.csdn.net/u014365862/article/details/78238 ...
- 求通俗讲解下tensorflow的embedding_lookup接口的意思
https://www.zhihu.com/question/48107602 作者:王凯链接:https://www.zhihu.com/question/48107602/answer/15980 ...
- 条件随机场 (CRF) 分词序列谈之一(转)
http://langiner.blog.51cto.com/1989264/379166 原创作品,允许转载,转载时请务必以超链接形式标明文章 原始出处 .作者信息和本声明.否则将追究法律责任.ht ...
- 强化Linux安全的10个技能
1.找出不必要的服务 很明显,服务器上跑的服务,并不是每个都有用的.强烈建议检查并关掉不需要的服务,从而减少风险(多跑一个服务,就可能多几个漏洞). 查询运行在runlevel 3的服务列表: [af ...
- Spark:JavaRDD 转化为 Dataset<Row>的两种方案
JavaRDD 转化为 Dataset<Row>方案一: 实体类作为schema定义规范,使用反射,实现JavaRDD转化为Dataset<Row> Student.java实 ...
- system函数的应用一例
system函数的应用一例
- oracle sqlldr使用(导入速度快,但对数据本身的处理功能弱)
oracle sqlldr使用(导入速度快,但对数据本身的处理功能弱) 博客分类: DB.Oracle OracleSQL sqlload.cmd pause sqlldr user/pass@tn ...
- iOS开发技巧 - 使用UISegmentedControl来对信息进行分组
(Swift) import UIKit class ViewController: UIViewController { var segmentedControl:UISegmentedContro ...
- 数据对接—kettle使用之四
上一篇介绍了表输出插件,并通过实例介绍插件的简单使用,如果有这样的需求大家可以参考一下并深入研究插件的其它细节设置.这一篇我们介绍和表输出对应的插件(表输入)的使用. 表输入: 1. 从步骤插入数据: ...
