关于matlab小记

目录：

1、函数取整

2、数据显示格式

3、三角函数运算

4、矩阵运算

5、函数句柄

6、二维函数图像绘制

7、符号对象

8、关于微积分

9、关于逻辑语句

10、关于运算符

───────────────────────────────────────────────────────────────────────────────────────────────────────

floor() 向下取整
ceil() 向上取整
round() 四舍五入到最近的整数
fix() 向零取整

───────────────────────────────────────────────────────────────────────────────────────────────────────

format long 显示15位双精度，7为单精度（scaled fixed point）
format short 显示5位(scaled fixed point format with 5 digits)
format short eng 至少5位加3位指数
format long eng16 位加至少3位指数
format hex 十六进制
format bank 2个十进制位
format + 正、负或零
format rat 有理数近似
format short 缺省显示
format long g 对双精度，显示15位定点或浮点格式，对单精度，显示7位定点或浮点格式。
format short g 5位定点或浮点格式
format short e 5位浮点格式
format long e 双精度为15位浮点格式，单精度为7为浮点格式

───────────────────────────────────────────────────────────────────────────────────────────────────────

matlab中三角函数sin、cos、tan等都是以弧度为单位的。
如果想用角度有两种方法。
一种是用sind、cosd、tand、atand等，他们是角度为单位的
另一种就是用deg2rad将角度转换为弧度。
下面是例子，四个式子的值是一样的。
sin(pi/6)
sind(30)
sin(deg2rad(30))
sind(rad2deg(pi/6))

───────────────────────────────────────────────────────────────────────────────────────────────────────

矩阵：

一般乘法 A*B

矩阵点乘（两矩阵的对应项相乘） A.*B

求矩阵的逆 inv(A)或A^-1

求矩阵的秩 rank(A)

求矩阵的迹trace(A)

───────────────────────────────────────────────────────────────────────────────────────────────────────

whos用于列出当前工作空间中所有变量，以及它们的名字、尺寸（比如一个矩阵或数组的行列维数）、所占字节数、属性等信息。这些信息都显示在matlab中的workspace窗口中。

───────────────────────────────────────────────────────────────────────────────────────────────────────

创建函数句柄一般语法格式：

Func_Handle = @Func_Filename;

　　①Func_Filename：函数所对应的M文件，或者matlab内部函数；

　　②Func_Handle：变量，保存函数句柄；

样例：

F_Handle = @cos
x =  : 0.25 * pi :  * pi
F_Handle(x)

函数句柄的好处：

　　①提高运行速度。因为matlab对函数的调用每次都是要搜索所有的路径，从set path中我们可以看到，路径是非常的多的，所以如果一个函数在你的程序中需要经常用到的话，使用函数句柄，对你的速度会有提高的。

　　②使用可以与变量一样方便。比如说，我再这个目录运行后，创建了本目录的一个函数句柄，当我转到其他的目录下的时候，创建的函数句柄还是可以直接调用的，而不需要把那个函数文件拷贝过来。因为你创建的function handles中，已经包含了路径。

───────────────────────────────────────────────────────────────────────────────────────────────────────

关于二维函数图形绘制：

绘制坐标轴的命令：

　plot 命令使用线性坐标空间绘制图形；

　loglog 命令在两个对数坐标空间中绘制图形；

　semilogx(或 semilogy)命令使用 x 轴（或 y 轴）为对数刻度，另外一个轴为线性刻度的坐标空间绘制图形；

　polar使用极坐标空间绘制图形。

plot函数的参数：

　　

　　

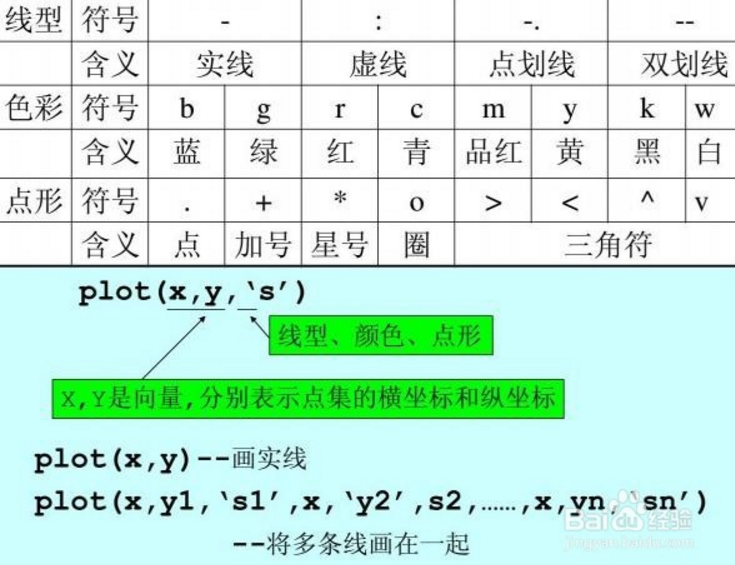
用法：

x=:0.25:;
y1=x.^0.1;
y2=x.^0.5;
y3=x.^0.8;
y4=x.^1.5;
t=:0.001:*pi;
hold on
plot(*cos(t),*sin(t),':')
plot(x,y1,'bo-',x,y2,'rH-')
plot(x,y3,'gp--')
plot(x,y4,'mx-.')
title('My Title'),xlabel('My X-axis Label'),ylabel('My Y-axis Label')
text(,,'Text for annotation')
grid
 
gtext('Text for annotation')

gtext命令是使用鼠标器定位的文字注释命令。当输入命令后，可以在屏幕上得到一个光标， 然后使用鼠标器控制它的位置。 按鼠标左键， 即可确定文字设定的位置。

hold on是图形保持命令，可以把当前图形保持在屏幕上不变，同时在这个坐标系内绘制另外一个图形，对应的命令为hold off。

axis([x-min,x-max,y-min,y-max])可以控制图形显示的坐标轴的范围。

axis square :  控制横纵坐标比例为1:1（输入axis(‘normal’)后返回一般状态）。

axis tight :  sets the axis limits to the range of the data.

───────────────────────────────────────────────────────────────────────────────────────────────────────

关于符号对象和符号表达式：

var = sym(A,flag)

A可以是数字、数值矩阵、数值表达式、字符串；

flag：

　　d：最接近的十进制浮点精确表示

　　e：（数值计算时）带估计误差的有理表示

　　f：十六进制浮点表示

　　r：默认设置时，最接近有理表示的形式

　　positive：限定A为正的实型符号变量

　　real：限定A为实型符号变量

syms a b c … flag；

───────────────────────────────────────────────────────────────────────────────────────────────────────

关于微积分：

1、求极限：

当计算lim(x->a)[f(x)]时，使用函数： limit((x - )/(x-),)

（注：没有标明x->a的参数a时，默认为零；x需要声明为符号对象）。

2、求微分：

syms x y
y = x^
diff(y)

3、求积分：

syms x
int(x * sin(x))
int(x * exp(x))
int(x * exp(x),,)
int(x)
int(x,,)

4、求解常微分方程（符号解法）：

　　r = dsolve( 'eqn1' , 'eqn2' , ... , 'cond1' , 'cond2' , ... , 'var' )

解释如下：eqni表示第i个微分方程，condi表示第i个初始条件，var表示微分方程中的自变量，默认为t。

样例：

syms x
dsolve('Dy = 3*x^2','x')  %计算"dy/dx = 3x^2"
dsolve('Dy = 3*x^2','y(0) = 2','x')  %计算"dy/dx = 3x^2",初始条件x=0时y=

[x,y]=dsolve('Dx=y','D2y-Dy=0','x(0)=1','y(0)=1','Dy(0)=1')

───────────────────────────────────────────────────────────────────────────────────────────────────────

关于逻辑语句：

if语句：

if <expression >
% Executes when the expression  is true
<statement(s)>
 
elseif <expression >
% Executes when the boolean expression  is true
<statement(s)>
 
elseif <expression >
% Executes when the boolean expression  is true
<statement(s)>
 
else
%  executes when the none of the above condition is true
<statement(s)>
 
end

例如：

a = ;
if(a<)
    fprintf('a < 10\n');
elseif(a<)
    fprintf('10 <= a <50\n');
elseif(a<)
    fprintf('50 <= a <80\n');
else
    fprintf('a >= 80\n');
end

while语句：

while <expression>
   <statements>
end

例如：

a = ;
while(a<)
    fprintf('now a = %d\n',a);
    a=a+;
end

for语句：

for a = :
   fprintf('now a = %d\n', a);
end
fprintf('\n');
for a = ::
   fprintf('now a = %d\n', a);
end
fprintf('\n');
for a = :-:
   fprintf('now a = %d\n', a);
end

break与continue的用法类似于C语言：

for a = :
   if(a == )
       continue;
   end
   fprintf('now a = %d\n', a);
end
 
fprintf('\n');
 
for a = :
   if(a == )
       break;
   end
   fprintf('now a = %d\n', a);
end

───────────────────────────────────────────────────────────────────────────────────────────────────────

关于运算符：

1、数学运算符

2、关系运算符

　　等于 ==

　　不等于 ~=

　　大于 >

　　大于等于 >=

　　小于 <

　　小于等于 <=

3、逻辑运算符

　　与：&

　　或：|

　　非：~