tensorflow入门 （一)

转载：作者：地球的外星人君
链接：https://www.zhihu.com/question/49909565/answer/207609620
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

分享一篇文章面向普通开发者的机器学习入门，作者@狸小华

前言

最近在摸索这方面相关的知识，本着整理巩固，分享促进的精神。所以有了这篇博文。

需要注意的是，本文受众：对机器学习感兴趣，且愿意花点时间学习的应用（业务）程序员

我本意是尽量简单，易于理解，快速上手，短时间能跑出来东西，这样子才能正向激励我们的学习欲望。

基于上述条件，需要你已经有一定的开发经验，微不足道的数学能力，以及善用搜索引擎的觉悟。开发环境搭建

开发环境搭建

首先，我希望你是Linux系用户,如果你是巨硬党，装一个VirtualBox吧，然后再装个ubuntu，由于我们只是入个门，对性能要求不高的。

机器学习相关的框架也很多，我这里选择了Keras，后端采用的Tensorflow 。那么理所当然的，会用到python来开发，没有python经验也莫慌，影响并不大。

1.ubuntu自带python 我就不介绍怎么安装了吧？

先安装pip(-dev
我用的python2.7，后文统一)打开你的终端，输入这个:(我建议更换下apt-get为国内镜像,安装完pip后也更换为国内镜像吧)

sudo apt-get install python-pip python

2.安装tensorflow和keras，matplotlib

还是打开终端，输入输入

mac端：

source activate ml_env27

>>conda install -c menpo menpoproject
>>pip install --upgrade tensorflow (use tensorflow-gpu if you want GPU support)
>>pip install -Iv keras==1.2.2 (make sure you install version 1.2.2)
>>conda install scikit-image h5py bidict psutil imageio
安装好依赖环境

python 测试

Python

import tensorflow as tf
hello = tf.constant('Hello, TensorFlow!')
sess = tf.Session()
print(sess.run(hello))

exit()

3.以后就用anconda配置好的环境配合pycharm来进行试验。

一些理论知识：

卷积神经网络CNN浅析

我建议你先把CNN当作一个黑盒子，不要关心为什么，只关心结果。

这里借用了一个分辨X和o的例子来这里看原文，就是每次给你一张图，你需要判断它是否含有"X"或者"O"。并且假设必须两者选其一，不是"X"就是"O"。

<img src="https://pic2.zhimg.com/50/v2-07b94113cd90697b17a3b149cff7f081_hd.png" data-rawwidth="725" data-rawheight="416" class="origin_image zh-lightbox-thumb" width="725" data-original="https://pic2.zhimg.com/v2-07b94113cd90697b17a3b149cff7f081_r.png">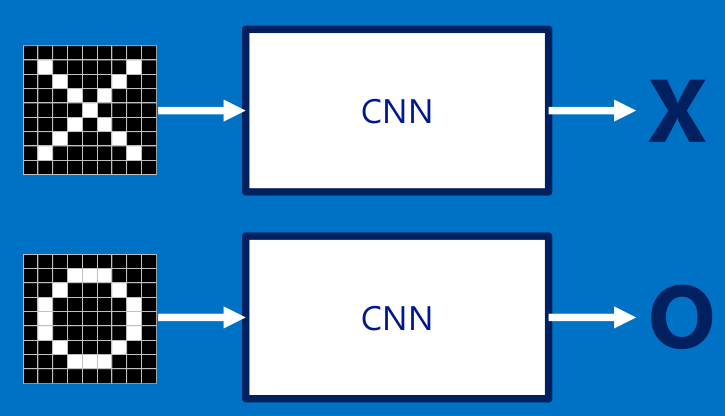

下面看一下CNN是怎么分辨输入的图像是x还是o，如果需要你来编程分辨图像是x还是o，你会怎么做？

可能你第一时间就想到了逐个像素点对比。但是，如果图片稍微有点变化呢？像是下面这个x，它不是标准的x，我们可以分辨它是x，

但是对于计算机而言，它就只是一个二维矩阵，逐个像素点对比肯定是不行的。

<img src="https://pic1.zhimg.com/50/v2-cc555b2db7b53159d41da4f6c9988610_hd.png" data-rawwidth="1208" data-rawheight="527" class="origin_image zh-lightbox-thumb" width="1208" data-original="https://pic1.zhimg.com/v2-cc555b2db7b53159d41da4f6c9988610_r.png">

CNN就是用于解决这类问题的，它不在意具体每个点的像素，而是通过一种叫卷积的手段，去提取图片的特征。

什么是特征?
特征就是我们用于区分两种输入是不是同一类的分辨点，像是这个XXOO的例子，如果要你描述X和O的区别，你会怎么思考？X是两条线交叉，O是封闭的中空的。。。

我们来看个小小的例子，如果下面两张图，需要分类出喜欢和不喜欢两类，那么你会提取什么作为区分的特征？(手动滑稽)

<img src="https://pic4.zhimg.com/50/v2-349af0484b75ab40928166d965aec783_hd.png" data-rawwidth="209" data-rawheight="160" class="content_image" width="209">

卷积层

所以对于CNN而言，第一步就是提取特征，卷积就是提取猜测特征的神奇手段。而我们不需要指定特征，任凭它自己去猜测，就像上图，

我们只需要告诉它，我们喜欢左边的，不喜欢右边的，然后它就去猜测，区分喜不喜欢的特征是黑丝，还是奶子呢？

<img src="https://pic1.zhimg.com/50/v2-389c7fe4b460d0c025c8413abfe5512c_hd.png" data-rawwidth="1211" data-rawheight="661" class="origin_image zh-lightbox-thumb" width="1211" data-original="https://pic1.zhimg.com/v2-389c7fe4b460d0c025c8413abfe5512c_r.png">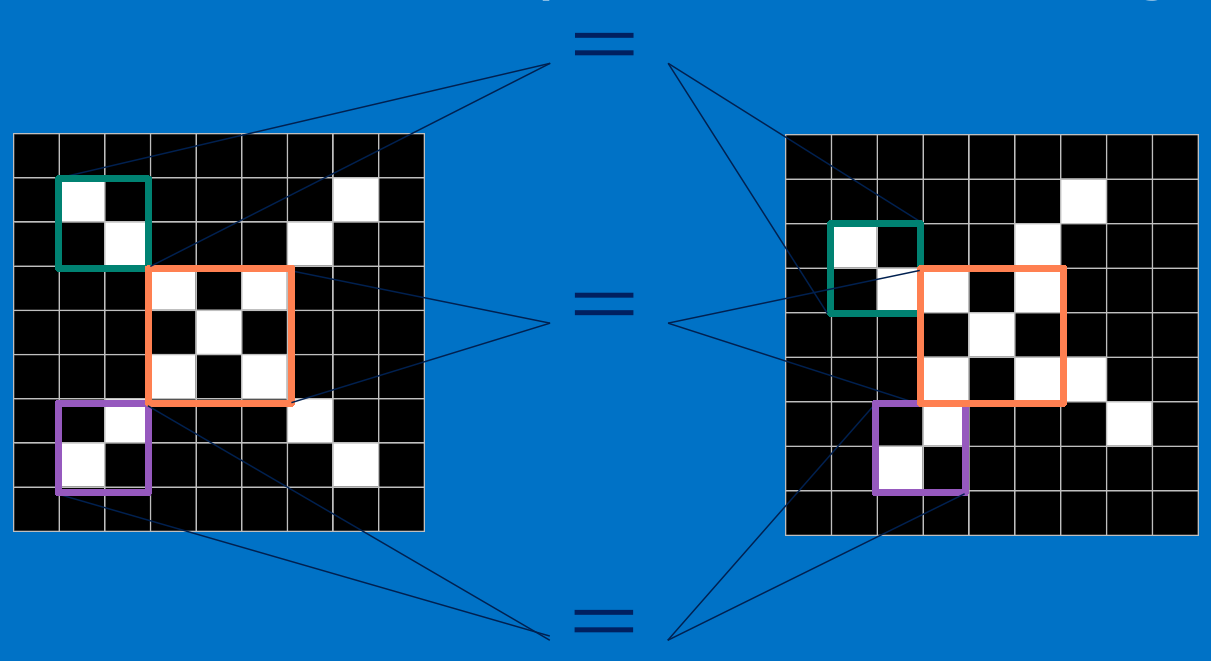

假设，我们上面这个例子，CNN对于X的猜测特征如上，现在要通过这些特征来分类。

计算机对于图像的认知是在矩阵上的，每一张图片有rgb二维矩阵（不考虑透明度）所以，一张图片，

应该是3x高度x宽度的矩阵。而我们这个例子就只有黑白，所以可以简单标记1为白，-1为黑。是个9x9的二维矩阵。

<img src="https://pic4.zhimg.com/50/v2-170b72d851cbf324cc09c0d1730efbaf_hd.png" data-rawwidth="1077" data-rawheight="310" class="origin_image zh-lightbox-thumb" width="1077" data-original="https://pic4.zhimg.com/v2-170b72d851cbf324cc09c0d1730efbaf_r.png">

我们把上面的三个特征作为卷积核(我们这里是假设已经训练好了CNN，训练提出的特征就是上面三个，我们可以通过这三个特征去分类 X )，去和输入的图像做卷积(特征的匹配)。

<img src="https://pic1.zhimg.com/50/v2-841bed5832b6d4bae2e22da73e77f99c_hd.png" data-rawwidth="394" data-rawheight="267" class="content_image" width="394">

<img src="https://pic4.zhimg.com/50/v2-c2c9d34affb2e12de57fc5542fd7be03_hd.png" data-rawwidth="395" data-rawheight="266" class="content_image" width="395">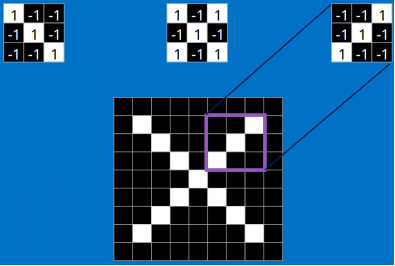

<img src="https://pic1.zhimg.com/50/v2-b6c5054d1be43bc293640f68f600cb14_hd.png" data-rawwidth="398" data-rawheight="265" class="content_image" width="398">

<img src="https://pic3.zhimg.com/50/v2-1edb7c99f28212c728b5c04cd7a3d9f2_hd.png" data-rawwidth="387" data-rawheight="259" class="content_image" width="387">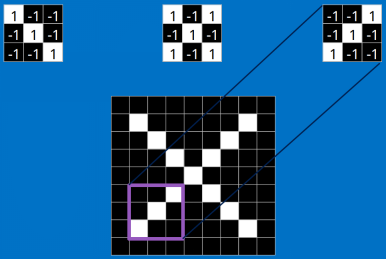

<img src="https://pic4.zhimg.com/50/v2-e39bbc74ac528680a6a14a23cbe280df_hd.png" data-rawwidth="386" data-rawheight="259" class="content_image" width="386">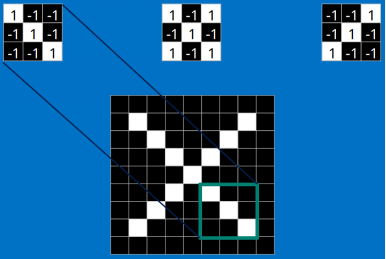

看完上面的，估计你也能看出特征是如何去匹配输入的，这就是一个卷积的过程，具体的卷积计算过程如下(只展示部分)：

<img src="https://pic1.zhimg.com/50/v2-eae07bcfbb079d9785a9bcb20436cc30_hd.png" data-rawwidth="954" data-rawheight="531" class="origin_image zh-lightbox-thumb" width="954" data-original="https://pic1.zhimg.com/v2-eae07bcfbb079d9785a9bcb20436cc30_r.png">

<img src="https://pic2.zhimg.com/50/v2-180debd15dc45f4fd095b8ebabf820e1_hd.png" data-rawwidth="956" data-rawheight="532" class="origin_image zh-lightbox-thumb" width="956" data-original="https://pic2.zhimg.com/v2-180debd15dc45f4fd095b8ebabf820e1_r.png">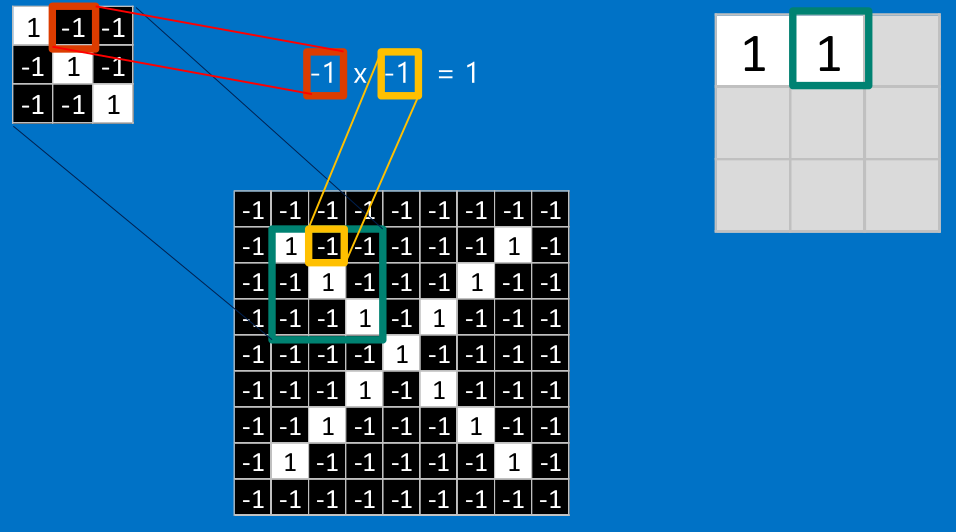

<img src="https://pic4.zhimg.com/50/v2-dbe766bfcc63774a9a59d0a0761a3e5f_hd.png" data-rawwidth="943" data-rawheight="531" class="origin_image zh-lightbox-thumb" width="943" data-original="https://pic4.zhimg.com/v2-dbe766bfcc63774a9a59d0a0761a3e5f_r.png">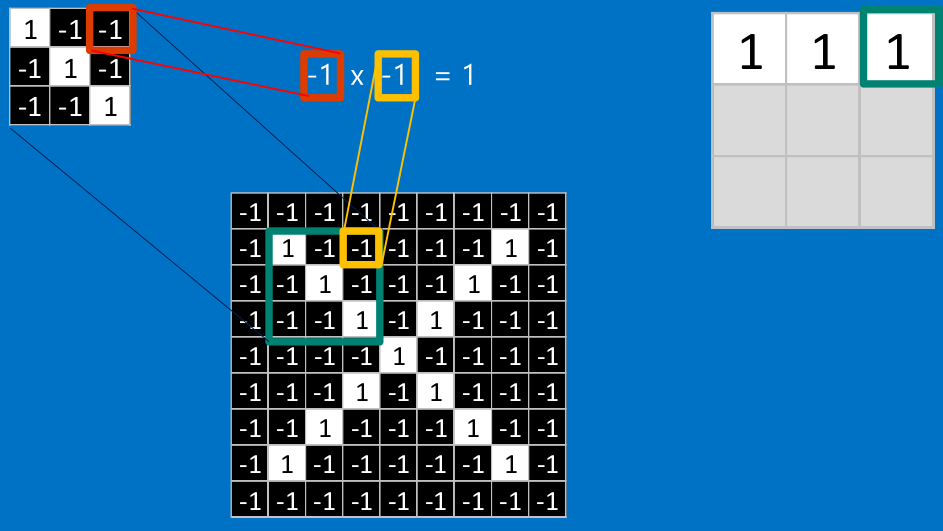

<img src="https://pic3.zhimg.com/50/v2-d744d1de3a4c9ec4214b52805ef70452_hd.png" data-rawwidth="950" data-rawheight="535" class="origin_image zh-lightbox-thumb" width="950" data-original="https://pic3.zhimg.com/v2-d744d1de3a4c9ec4214b52805ef70452_r.png">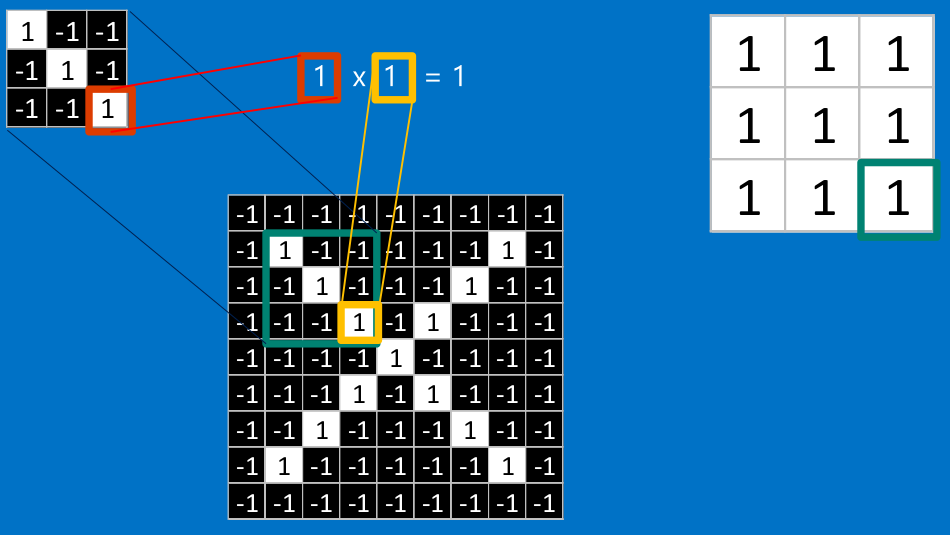

把计算出的结果填入新的矩阵

<img src="https://pic4.zhimg.com/50/v2-ff5a99b11326ec90e42257479fb0a597_hd.png" data-rawwidth="1133" data-rawheight="535" class="origin_image zh-lightbox-thumb" width="1133" data-original="https://pic4.zhimg.com/v2-ff5a99b11326ec90e42257479fb0a597_r.png">

其他部分也是相同的计算

<img src="https://pic3.zhimg.com/50/v2-dd011652f998e6a621eae0cd991cacfe_hd.png" data-rawwidth="953" data-rawheight="532" class="origin_image zh-lightbox-thumb" width="953" data-original="https://pic3.zhimg.com/v2-dd011652f998e6a621eae0cd991cacfe_r.png">

<img src="https://pic4.zhimg.com/50/v2-f6d277f4d8dc9fcd2ef3b4549ae6da93_hd.png" data-rawwidth="1145" data-rawheight="523" class="origin_image zh-lightbox-thumb" width="1145" data-original="https://pic4.zhimg.com/v2-f6d277f4d8dc9fcd2ef3b4549ae6da93_r.png">

最后，我们整张图用卷积核计算完成后：

<img src="https://pic4.zhimg.com/50/v2-b52238a119466319f83668010efbc5db_hd.png" data-rawwidth="1120" data-rawheight="409" class="origin_image zh-lightbox-thumb" width="1120" data-original="https://pic4.zhimg.com/v2-b52238a119466319f83668010efbc5db_r.png">

三个特征都计算完成后：

<img src="https://pic2.zhimg.com/50/v2-57d763b9349b1dc945bb7083035cc361_hd.png" data-rawwidth="856" data-rawheight="602" class="origin_image zh-lightbox-thumb" width="856" data-original="https://pic2.zhimg.com/v2-57d763b9349b1dc945bb7083035cc361_r.png">

不断地重复着上述过程，将卷积核（特征）和图中每一块进行卷积操作。最后我们会得到一个新的二维数组。

其中的值，越接近为1表示对应位置的匹配度高，越是接近-1，表示对应位置与特征的反面更匹配，而值接近0的表示对应位置没有什么关联。

以上就是我们的卷积层，通过特征卷积，输出一个新的矩阵给下一层。

池化层

在图像经过以上的卷积层后，得到了一个新的矩阵，而矩阵的大小，则取决于卷积核的大小，和边缘的填充方式，总之，在这个XXOO的例子中，我们得到了7x7的矩阵。池化就是缩减图像尺寸和像素关联性的操作，只保留我们感兴趣（对于分类有意义）的信息。

常用的就是2x2的最大池。

<img src="https://pic1.zhimg.com/50/v2-1819a146f4df7a1a764a4fa99f7ee4e0_hd.png" data-rawwidth="971" data-rawheight="466" class="origin_image zh-lightbox-thumb" width="971" data-original="https://pic1.zhimg.com/v2-1819a146f4df7a1a764a4fa99f7ee4e0_r.png">

<img src="https://pic2.zhimg.com/50/v2-274c2a16a6b519c3d480828628bcdfb9_hd.png" data-rawwidth="959" data-rawheight="459" class="origin_image zh-lightbox-thumb" width="959" data-original="https://pic2.zhimg.com/v2-274c2a16a6b519c3d480828628bcdfb9_r.png">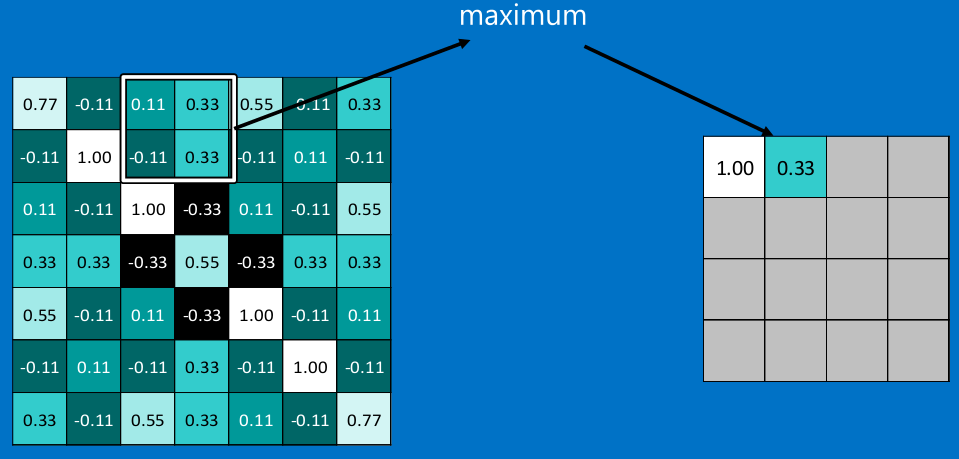

<img src="https://pic2.zhimg.com/50/v2-0e6cad2ee49abcf6baf202b8a09ead45_hd.png" data-rawwidth="963" data-rawheight="458" class="origin_image zh-lightbox-thumb" width="963" data-original="https://pic2.zhimg.com/v2-0e6cad2ee49abcf6baf202b8a09ead45_r.png">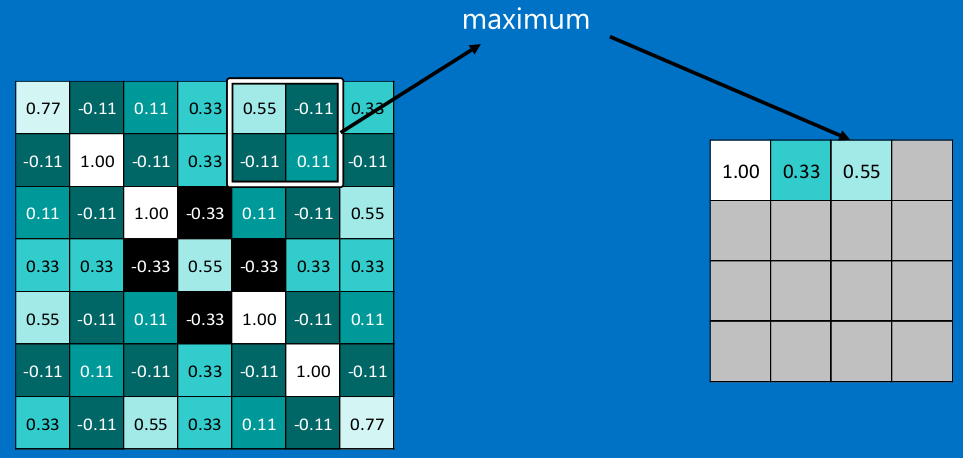

<img src="https://pic4.zhimg.com/50/v2-f7e608bfa6a8da46db8073950e4d32e3_hd.png" data-rawwidth="962" data-rawheight="458" class="origin_image zh-lightbox-thumb" width="962" data-original="https://pic4.zhimg.com/v2-f7e608bfa6a8da46db8073950e4d32e3_r.png">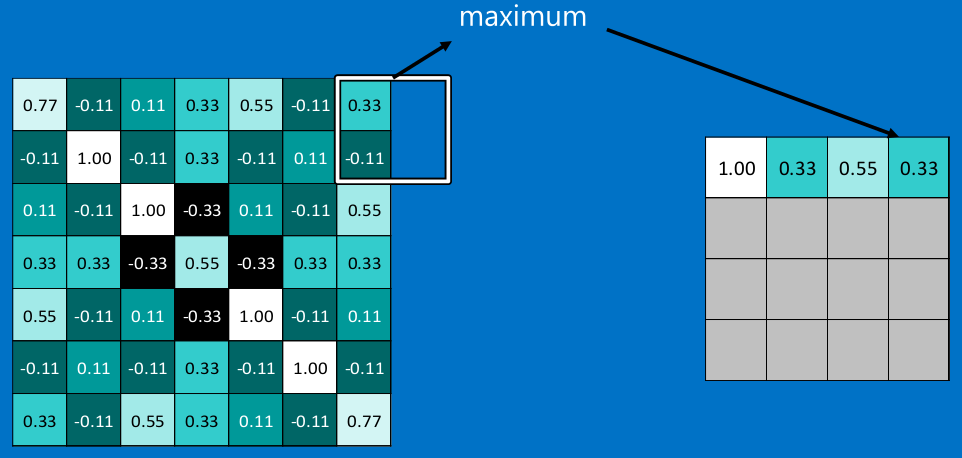

看完上面的图，你应该知道池化是什么操作了。

通常情况下，我们使用的都是2x2的最大池，就是在2x2的范围内，取最大值。因为最大池化（max-pooling）保留了每一个小块内的最大值，所以它相当于保留了这一块最佳的匹配结果（因为值越接近1表示匹配越好）。这也就意味着它不会具体关注窗口内到底是哪一个地方匹配了，而只关注是不是有某个地方匹配上了。

这也就能够看出，CNN能够发现图像中是否具有某种特征，而不用在意到底在哪里具有这种特征。这也就能够帮助解决之前提到的计算机逐一像素匹配的死板做法。

<img src="https://pic2.zhimg.com/50/v2-f707d3d2a2bacec1e40822a9473a3779_hd.png" data-rawwidth="818" data-rawheight="587" class="origin_image zh-lightbox-thumb" width="818" data-original="https://pic2.zhimg.com/v2-f707d3d2a2bacec1e40822a9473a3779_r.png">

同样的操作以后，我们就输出了3个4x4的矩阵。

全连接层

全连接层一般是为了展平数据，输出最终分类结果前的归一化。 我们把上面得到的4x4矩阵再卷积+池化，得到2x2的矩阵

<img src="https://pic2.zhimg.com/50/v2-9c967ec12fa4a969245de0ae7118bab9_hd.png" data-rawwidth="590" data-rawheight="491" class="origin_image zh-lightbox-thumb" width="590" data-original="https://pic2.zhimg.com/v2-9c967ec12fa4a969245de0ae7118bab9_r.png">

全连接就是这样子，展开数据，形成1xn的'条'型矩阵。

<img src="https://pic3.zhimg.com/50/v2-b833cf3280c2f12b6f50e6bf1ce48e3a_hd.png" data-rawwidth="1123" data-rawheight="485" class="origin_image zh-lightbox-thumb" width="1123" data-original="https://pic3.zhimg.com/v2-b833cf3280c2f12b6f50e6bf1ce48e3a_r.png">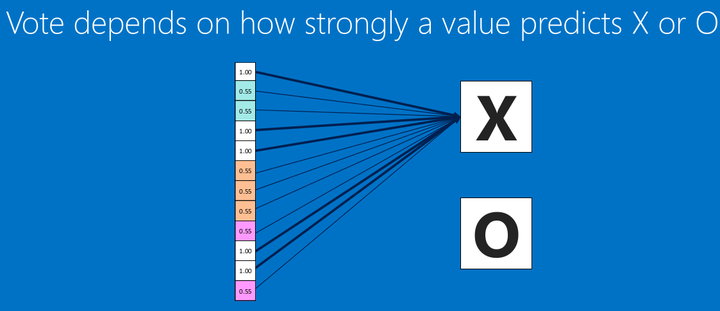

然后再把全连接层连接到输出层。之前我们就说过，这里的数值，越接近1表示关联度越大，然后我们根据这些关联度，分辨到底是O还是X.

<img src="https://pic4.zhimg.com/50/v2-e691bc8d06106b63539b280bd134c063_hd.png" data-rawwidth="1042" data-rawheight="517" class="origin_image zh-lightbox-thumb" width="1042" data-original="https://pic4.zhimg.com/v2-e691bc8d06106b63539b280bd134c063_r.png">

<img src="https://pic3.zhimg.com/50/v2-6840898a5893c31f77c89bcd539b4922_hd.png" data-rawwidth="996" data-rawheight="494" class="origin_image zh-lightbox-thumb" width="996" data-original="https://pic3.zhimg.com/v2-6840898a5893c31f77c89bcd539b4922_r.png">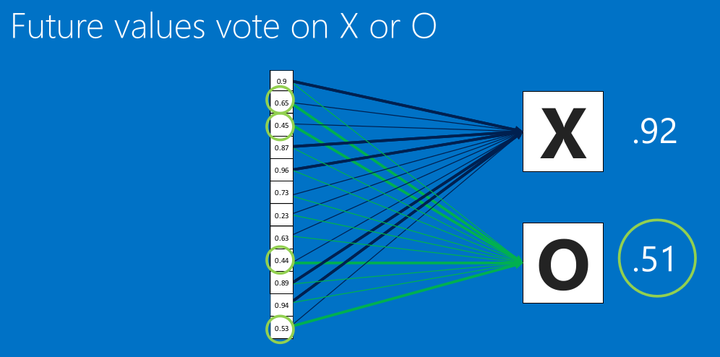

看上图（圈圈里面的几个关键信息点），这里有个新的图像丢进我们的CNN了，根据卷积>池化>卷积>池化>全连接的步骤，我们得到了新的全连接数据，然后去跟我们的标准比对，得出相似度，可以看到，相似度是X的为0.92 所以，我们认为这个输入是X。

一个基本的卷积神经网络就是这样子的。回顾一下，它的结构：

<img src="https://pic1.zhimg.com/50/v2-a1722f82172c24581f79c38c46f8a08c_hd.png" data-rawwidth="1186" data-rawheight="543" class="origin_image zh-lightbox-thumb" width="1186" data-original="https://pic1.zhimg.com/v2-a1722f82172c24581f79c38c46f8a08c_r.png">

Relu是常用的激活函数，所做的工作就是max(0,x)，就是输入大于零，原样输出，小于零输出零，这里就不展开了。

CNN实现手写数字识别

感觉，这个mnist的手写数字，跟其他语言的helloworld一样了。我们这里来简单实现下。首先，我建议你先下载好数据集，keras的下载太慢了（下载地址）。

下载好以后，按下面的位置放，你可能要先运行下程序，让他自己创建文件夹，不然，你就手动创建吧。

<img src="https://pic3.zhimg.com/50/v2-7bb39062bb6807c9d8fbdf706770cb26_hd.png" data-rawwidth="396" data-rawheight="239" class="content_image" width="396">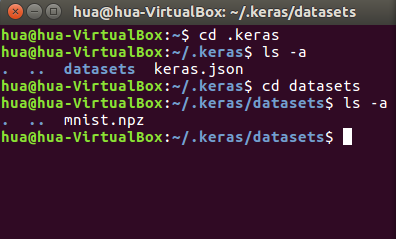

新建个python文件，test.py然后输入下面的内容

#coding: utf- from keras.datasets import mnist
import matplotlib.pyplot as plt
# 加载数据
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# 展示下第一张图
plt.imshow(X_train[], cmap=plt.get_cmap('PuBuGn_r'))
plt.show()

运行后出来张图片，然后关掉就行，这里只是看看我们加载数据有没有问题。

x_train,x_test是我们的图像矩阵数据，是28x28大小，然后有12500条吧好像。然后y_train,y_test都是标签数据，标明这张图代表是数字几。

#coding: utf- #Simple CNN import numpy
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout
from keras.layers import Flatten
from keras.layers.convolutional import Conv2D
from keras.layers.convolutional import MaxPooling2D
from keras.utils import np_utils

seed =
numpy.random.seed(seed)

#加载数据
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# reshape to be [samples][channels][width][height] X_train = X_train.reshape(X_train.shape[],, ,).astype('float32')
X_test = X_test.reshape(X_test.shape[],, ,).astype('float32')

# normalize inputs from - to - X_train = X_train /  X_test = X_test /  # one hot encode outputs y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
num_classes = y_test.shape[]

# 简单的CNN模型
def baseline_model():
    # create model model = Sequential()
    #卷积层
    model.add(Conv2D(, (, ), padding='valid', input_shape=(, ,), activation='relu')) #池化层
    model.add(MaxPooling2D(pool_size=(, )))
    #卷积
    model.add(Conv2D(, (, ), padding='valid' ,activation='relu')) #池化
    model.add(MaxPooling2D(pool_size=(, )))
    #全连接，然后输出
    model.add(Flatten())
    model.add(Dense(, activation='relu'))
    model.add(Dense(num_classes, activation='softmax')) # Compile model
    model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
    return model

# build the model model = baseline_model()

# Fit the model
model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=, batch_size=, verbose=)

代码也挺简单，因为keras也是封装的挺好的了。基本你看懂了前面的就没问题。

Epoch / 3s - loss: 0.2791 - acc: 0.9203 - val_loss: 0.1420 - val_acc: 0.9579
Epoch / 3s - loss: 0.1122 - acc: 0.9679 - val_loss: 0.0992 - val_acc: 0.9699
Epoch / 3s - loss: 0.0724 - acc: 0.9790 - val_loss: 0.0784 - val_acc: 0.9745
Epoch / 3s - loss: 0.0509 - acc: 0.9853 - val_loss: 0.0774 - val_acc: 0.9773
Epoch / 3s - loss: 0.0366 - acc: 0.9898 - val_loss: 0.0626 - val_acc: 0.9794
Epoch / 3s - loss: 0.0265 - acc: 0.9930 - val_loss: 0.0639 - val_acc: 0.9797
Epoch / 3s - loss: 0.0185 - acc: 0.9956 - val_loss: 0.0611 - val_acc: 0.9811
Epoch / 3s - loss: 0.0150 - acc: 0.9967 - val_loss: 0.0616 - val_acc: 0.9816
Epoch / 4s - loss: 0.0107 - acc: 0.9980 - val_loss: 0.0604 - val_acc: 0.9821
Epoch / 4s - loss: 0.0073 - acc: 0.9988 - val_loss: 0.0611 - val_acc: 0.9819

然后你就能看到这些输出，acc就是准确率了，看后面的val_acc就行。