二叉树总结(五)伸展树、B-树和B+树

一、伸展树

伸展树(Splay Tree)是一种二叉排序树，它能在O(log n)内完成插入、查找和删除操作。

因为，它是一颗二叉排序树，所以，它拥有二叉查找树的性质；除此之外，伸展树还具有的一个特点是：当某个节点被访问时，伸展树会通过旋转使该节点成为树根。这样做的好处是，下次要访问该节点时，能够迅速的访问到该节点。但是，它并不是单纯的把访问的节点放

到树根就完了，它还能减少该节点的访问路径上的节点的深度。

假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小，被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法，在每次查找之后对树进行重构，把被查找的条目搬移到离树根近一些的地方。伸展树应运而生，它是一种自

调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

伸展树保证从空树开始的任意连续的m次对树的操作最多话费花费O(mlogn)时间（n是节点数）；因此，它不存在坏的输入序列。

自底向上伸展树

伸展树包含之字形和一字型两种情形。

之字形情况

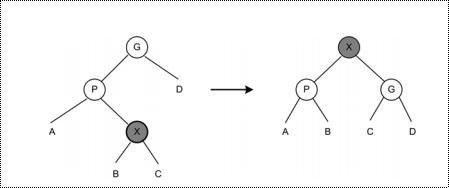
找到的节点是X时，类似平衡二叉树中的LR旋转的情况，可以将X变成树根；

一字型情况

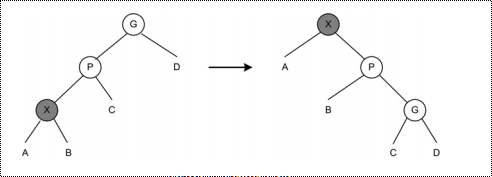
找到的节点是X时，类似平衡二叉树中的LL旋转的情况，使用两次LL旋转时就可以将X变成树根；

P(X) : 获得X的父节点，G(X) : 获得X的祖父节点（=P(P(X))）。
Function Buttom-up-splay:
    Do
        If X 是 P(X) 的左子结点 Then
            If P（X）是G（X）的左子结点
                P(X) 绕G(X)右旋
            Endif
            X 绕P(X)右旋
        Else If X 是 P(X) 的右子结点 Then
            If P（X）是G（X）的右子结点
                P(X) 绕G(X)左旋
            Endif
            X 绕P(X)左旋
        Endif
    While (P(X) != NULL)
EndFunction

自顶向下伸展树

在自底向上的伸展树中，我们需要求一个节点的父节点和祖父节点，因此这种伸展树难以实现。因此，我们可以构建自顶向下的伸展树。

当我们沿着树向下搜索某个节点X的时候，我们将搜索路径上的节点及其子树移走。我们构建两棵临时的树──左树和右树。没有被移走的节点构成的树称作中树。在伸展操作的过程中：

1. 当前节点X是中树的根。
2. 左树L保存小于X的节点。
3. 右树R保存大于X的节点。

基本的zig旋转

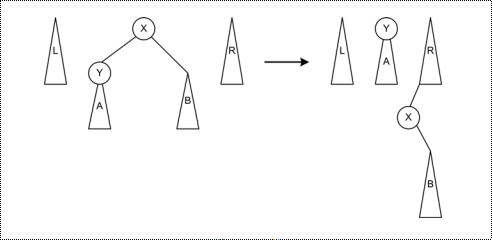
类似LL旋转，将X的子树放到R树上。

zig-zag旋转

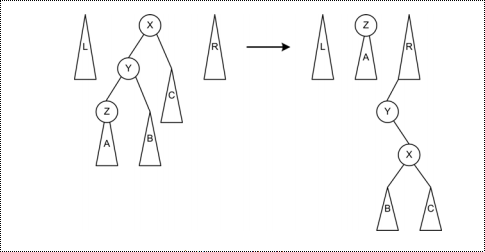
两次LL旋转，将Z变成树根，注意，第二次旋转B的位置是，变成X的右子树；

以上是左旋转的情况，它会把路径上的节点放到R树上，如果是右旋转，则它会把路径上的节点类似的挂到L树上。

合并

最后当找到目标节点时，合并L树、中树、R树。

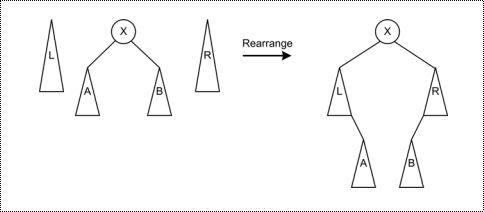
只需要将目标节点当做树根，L树当做目标节点的左子树，目标节点的原左子树放到L树的右子树；同理R树作为目标节点的右子树，原目标节点的右子树作为R树的左子树。

二、B-树

定义：

一棵m阶B-树是拥有以下性质的多路查找树：

1. 非叶子结点的根结点至少拥有两棵子树；
2. 每一个非根且非叶子的结点含有k－1个关键字以及k个子树，其中⌈m/2⌉≤k≤m；

3. 非叶子结点的关键字个数=指向儿子的指针个数-1；

4. 非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

5. 非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

6. 所有的叶子结点都在同一层。

B-树的特性：

1. 关键字集合分布在整颗树中；
2. 任何一个关键字出现且只出现在一个结点中；
3. 搜索有可能在非叶子结点结束；
4. 其搜索性能等价于在关键字全集内做一次二分查找；
5. 自动层次控制；

下图是一颗3阶B-树：

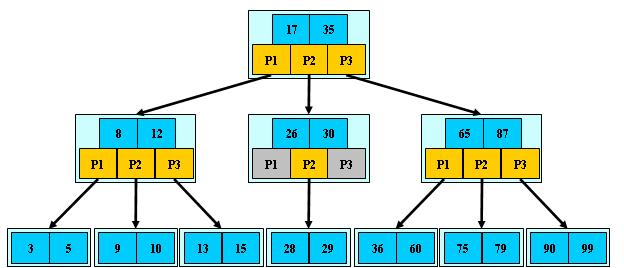
插入

删除

应用

• B-tree索引是数据库中存取和查找文件(称为记录或键值)的一种方法。
• 硬盘中的结点是B-tree结构的

实现

参考：https://www.roading.org/algorithm/introductiontoalgorithm/b-%E6%A0%91%E7%9A%84c%E5%AE%9E%E7%8E%B0.html

三、B+树

其定义基本与B-树同，除了：

1. 非叶子结点的子树指针与关键字个数相同；
2. 非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B-树是开区间）；
3. 为所有叶子结点增加一个链指针；
4. 所有关键字都在叶子结点出现；

B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；
B+的特性：

• 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
• 不可能在非叶子结点命中；
• 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
• 更适合文件索引系统；

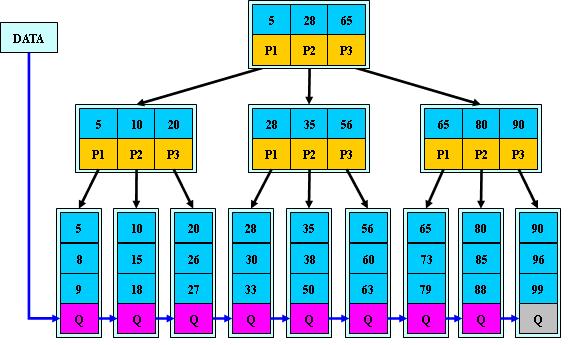
查找

应用