GAN算法笔记

本篇文章为Goodfellow提出的GAN算法的开山之作"Generative Adversarial Nets"的学习笔记，若有错误，欢迎留言或私信指正。

1. Introduction

GAN模型解决的问题

作者在首段指出了本课题的意义——能够避免深度生成模型中的两个局限性：

（1）最大似然估计等相关策略中难以处理的概率计算；

（2）在生成环境中难以利用分段线性单元的优势。

PS：深度生成模型是为了从原始的样本数据中模拟出数据分布，进而产生符合这一分布的新的样本。

GAN模型的构成

GAN模型主要分为两个部分：生成模型$G$(generative model)和判别模型$D$(discriminative model)。作者将这两个部分的关系类比为假币制造商和警察。判别模型（警察）来判断一个样本究竟是来自于数据分布还是模型分布，而生成模型（假币制造商）则是为了生成假的样本来骗过判别模型（警察）。这样产生的竞争驱使两方都不断更新自己的方法，直到假样本与真样本完全无法区分。框架中的生成模型通过将随机噪声输入多层感知机进而得到假样本，而判别模型则是将样本输入多层感知机来判断样本是否为真实样本。作者指出，同时训练这两个模型的方法是使用反向传播算法(backpropagation algorithm)和丢弃算法（应该是“随机失活算法”，之前表述有所错误）(dropout algorithm)。

ps：多层感知机(Multi Layer Perceptron) 为如下图所示的包括至少一个隐藏层（除去一个输入层和一个输出层以外）的多层神经元网络。

2. Related work

作者在这一部分介绍了有关深度生成网络的相关工作，由于还没有系统掌握深度学习，暂且跳过。。。

3. Adversarial nets

作者定义了两个函数：

$G\left(\boldsymbol{z} ; \theta_{g}\right)$表示从噪音$\boldsymbol{z}$到数据样本空间的映射函数，其中$\theta_{g}$表示多层感知机的参数。
$D(\boldsymbol{x};\theta_d)$表示对于输入样本$\boldsymbol{x}$输出判断为真实数据的概率（为一个标量）

GAN的目标

作者将GAN的目标定义为下面这个优化公式：

\[\min_G \max_D V(D,G)=\mathbb{E}_{\mathbf{x}\sim p_{data}(x)}[\log D(x)]+\mathbb{E}_{\mathbf{z}\sim p_z}[\log (1-D(G(z)))]
\]

这个公式由两部分构成，前一部分 $\mathbb{E}_{\mathbf{x}\sim p_{data}(x)}[\log D(x)]$ 可以理解为判别模型正确判定真实数据的对数期望，后一部分$\mathbb{E}_{\mathbf{z}\sim p_z}[\log (1-D(G(z)))]$可以理解为判别模型正确识别假样本的对数期望。

相对熵？

后面重新看这个公式的时候突然想到一个问题：为什么公式中求期望时要在概率值的外面再套一个log函数呢？

还没有完全想明白，感觉有点像是交叉熵和相对熵的概念，但是又无法将上述公式和相对熵的公式定义一一对应起来。

可以先可以参考这个链接：机器学习中的各种“熵”（这个博客页面是真的卡）

后面作者在Theoretical Results部分果然用到了交叉熵的概念，用来证明这个公式的目标就是实现$p_g=p_{data}$

图形理解

下面这张图我看了一晚上没看懂，今天早上才明白是什么意思。

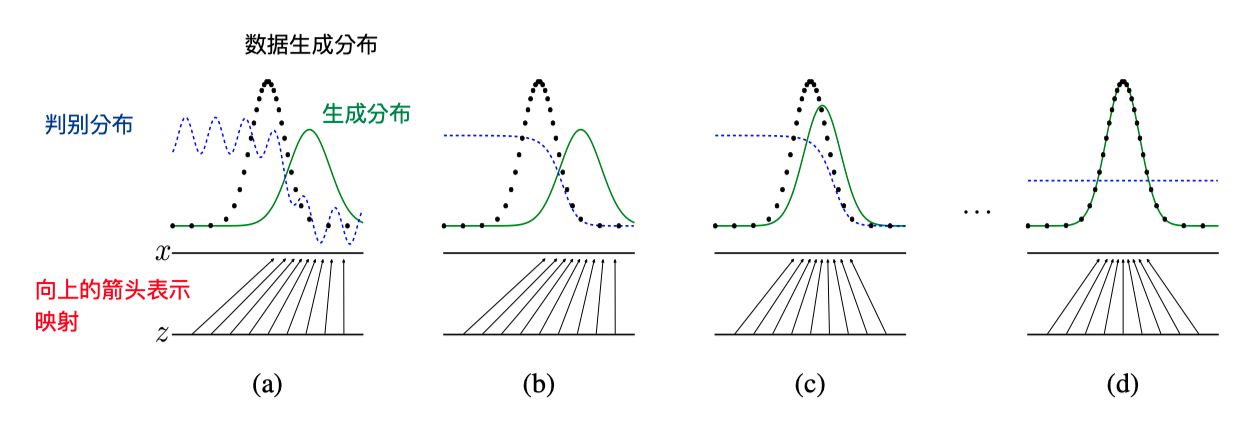
图中蓝色的虚线表示判别模型的概率分布，黑色的点线表示原始数据的概率分布，绿色实线表示生成模型的生成概率分布。

图(a)中表示训练还未开始或刚开始一段时间时，判别模型和生成模型都还没有经过大量的训练，因此判别概率分布还有些波动，生成分布距离真实数据生成分布还有不小的距离。
图(b)表示经过一段时间的训练后，判别模型可以较好的判别出原始样本和生成样本，蓝色虚线的高度表示当前位置对应横坐标的样本为真实数据样本的概率，越高表示为真实样本的概率越大。
图(c)表示继续训练一段时间之后，原始样本和生成样本更加接近，判别模型还是有相对不错的判别效果。
图(d)表示经过足够的训练之后，原始样本与生成样本的概率分布特征基本一致，判别模型失去判别效果。

算法1

算法1原文描述

算法1中文python伪代码描述（这是个什么鬼东西）

for i in range(训练的迭代次数)):

    for j in range(k步):

        从噪音分布中取出m个噪音样本

        从数据分布中取出m个样本

        利用随机梯度上升法更新判别器D

    从噪音分布中取出m个噪音样本

    利用随机梯度下降法更新生成器G

4. Theoretical Results

全局最优$p_g=p_{data}$

作者给出了第一个命题：当生成模型$G$固定时，最优判别器为：$$D^*G(x)=\frac{p{data}(x)}{p_{data}(x)+p_g(x)}$$

并且作者也给出了证明，证明的思路很简单，形如$y \rightarrow a \log (y)+b \log (1-y)$的式子在$[0,1]$区间内有固定的最大值为$\frac{a}{a+b}$。

这样一来，原公式就可以替换成下式：

\[\begin{aligned} C(G) &=\max _{D} V(G, D) \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{z}}\left[\log \left(1-D_{G}^{*}(G(\boldsymbol{z}))\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \frac{p_{g}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right] \end{aligned}
\]

再利用KL散度（相对熵）公式：

\[D_{KL}(P||Q)=\sum_{i=1}^np_i\log (\frac{p_i}{q_i})
\]

可以将刚刚的式子替换为

\[C(G)=V(G^*,D)=-\log (4)+K L\left(p_{\text {data }} \| \frac{p_{\text {data }}+p_{g}}{2}\right)+K L\left(p_{g} \| \frac{p_{\text {data }}+p_{g}}{2}\right)
\]

进一步可以利用JS散度公式进行替换：

\[C(G)=-\log (4)+2 \cdot J S D\left(p_{\mathrm{data}} \| p_{g}\right)
\]

由JS散度公式的性质——即取值范围为$[0,1]$因此可知$C(G)$的最小值为$-\log (4)$，此时JS散度公式取0，并且此时唯一解为$p_g=p_{data}$

5. Experiments

6. Advantages and disadvantages

作者指出，生成式对抗网络有以下四个优势：

根据实验结果来看，比其他模型产生了更锐利、清晰的样本。
生成式对抗网络能够被用来训练任何一种生成器网络。
不需要设计遵循任何种类的因式分解的模型。
无需利用马尔可夫链反复采样，回避了棘手的近似计算的概率问题。

GAN目前存在的主要问题是：

解决不收敛的问题