[转]講講 John Carmack 的快速反平方根演算法

講講 John Carmack 的快速反平方根演算法

 原地址http://213style.blogspot.com/2014/07/john-carmack.html

本篇的主題很簡單，講講怎麼快速計算 反平方根

 

圖1. 反平方根函數，但是要如何快速計算此式呢？

 

反平方根運算在 3D 圖形領域占有重要地位，主要用於計算 光源 與 反射，運算過程中

需要計算 Normalized Vector，這時就需要進行反平方根運算，因為在 1990 年以前可沒有

特殊的硬體可以直接處理 T&L，直到有名的 GeForce 256 出現才改觀，而 3D 遊戲內某些

可以貫穿多個敵人的武器，也需要用到反平方根運算，所以該運算不只出現在與繪圖有關

的部分，一些與圖形無關的演算法也會用到，所以大部分 3D 遊戲中，都還是會存在獨立的

反平方根函式。在數值計算領域裡，反平方根計算可以間接取得平方根的值，例如在 8051

這類只能運算整數的微處理器，要計算平方根就會用到反平方根運，因為 反平方根運 存在

快速演算法，其中最有名的就是在 Quake III 裡面的 Q_rsqrt 函式，這個函式非常有名，大不

分的 反平方根運算 都是直接把這段函式的原始碼直接貼到自己的程式內，然後在根據

需要修改，例如要用於 8051 內就還得需要加上定點化的技巧，目前顯示卡內硬體的反平方根

運算正是 Q_rsqrt 演算法硬體化的結果，所以先來看看這段在 Quake III 內 Q_rsqrt 的原始碼：

 

圖 2. 位於 Quake III 內的 Q_rsqrt 函式原始碼

中文註解部分是在下加上。

 

整個函式包含兩個部分：

 

第一部分， 從 整數運算 得到 一個已經 靠近解的初始值

第二不分， 利用 Newton-Raphson 方法疊代增加解的精度

 

該函式內演算法精髓的部分是在 第一部分 用整數運算取得求解所需的初始值，第二部分

到沒甚麼，有學過數值方法的讀著應該可以很輕易的看懂，但是對於沒有學過的讀者，在下

講完第一部分之後，會稍微提一下 Newton-Raphson 求解法，因為第二部分並非重點，理解

第一部分才是重點所在，第一部分用到的技巧涉及必須理解浮點數的存放結構與表達，所以

先看看浮點數怎麼存放在電腦中。

 

 

 

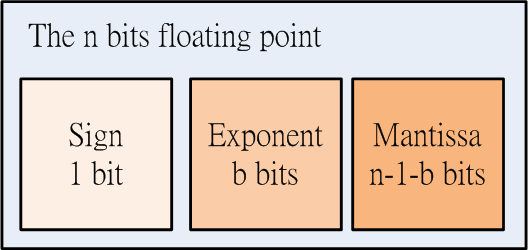
圖 3. 一個 n bits 的浮點數的存放結構

 

圖 4. 一個浮點數的表達

 

 

圖 3. 顯示了 一個浮點數如何存放在記憶體內，有時候又稱 floating-point bits level，各位讀者

可以看到一個端倪，其實浮點數也是一種整數，或者說每個浮點數都有獨一無二的整數映射

而圖 4. 說明了 浮點運算器怎麼解讀一個整數為浮點數的方式，由於反平方根不能有負值

所以圖 4. 中的 s 必須等於 0，因此就可以不用考慮浮點數的符號位元，剛剛前面有提到

其實浮點數也是一種整數，也就是說，假如圖 3. 的浮點數存放結構 改用整數的觀點來看

其實就是

 

圖 5.  浮點數 與 整數 的對應關係

 

圖 5. 說明 一個浮點數 與 對應的整數之間總是存在 唯一的對應關係，因此，可以將

浮點數映至對應的整數，從整數的觀點進行運算，要執行這個技巧之前，先以浮點數

觀點對兩邊做 Binary Logarithm，也就是兩邊取 2 為基底的 log 函數：

 

圖 6. 對兩邊取 log2，且 y 與 x 皆代入圖 4. 的方程式

 

圖 6. 將 y 與 x 皆拆解為 mantissa 與 exponent 表達，剩下的工作就是要找出 從整數觀點表達

的 y 與 x 之間的關係，所以必須想辦法先把 log2 弄掉，才能夠套用圖 5. 內的恆等式，而

圖 4. 裡面的浮點數表達式中的 m 是一個大於等於 0 小於 1 的數值，所以圖 6. 中要把 log2

拿掉 可以用 近似公式

 

圖 7. 近似的 binary logarithm 公式

 

如圖 7. 所示，利用近似 Binary Logarithm 公式，可以將圖 6. 中的 log 函數拿掉，用近似公式

替換，這個近似的步驟很重要，透過這個步驟才能夠獲得才能夠獲得等價於圖 1. 的整數

運算公式，其 圖 8. 顯示了完整的推導過程。

 

圖 8. 用整數運算式表達近似反平方根運算

 

圖 8. 最後一條公式就是這個演算法最重要的結論，這條整數運算的結果就是反平方根

用整數運算表達的形式，所以最終的結論可以用圖 9. 來解釋。

 

圖 9. 最終結論解釋了圖 1. 中神秘的轉換運算的理由，可以看到

該方法厲害之處在於 Iy 轉回浮點數觀點看，其實已經是近似解

這個近似解就是最好的初始值，後面套用牛頓法只是為了增加解的精度

 

有了圖 9. 最終結論，要理解圖 1. 中 16 進位值 5F3759DF 就很簡單，只要將 B、L 與 sigma

的數值代入圖 9. 的反平方根近似整數演算法就會得到這個 魔術數字。

 

圖 10. 神秘的 0x5F3759DF 魔術數字其實只是 32-bit 浮點

代入反平方根整數演算法所得到的結果，而且 sigma 可調

該魔術數字可能會有些微的變化

 

 

圖 10. 解釋了 John Carmack 快速反平方根演算法內 Magic Number 的由來，由於在下

是直接以 n 位元浮點數推導，讀者也可以去找一找 double floating 的值會是多少

演算法後面的部分前面有提到，其實沒有甚麼值得研究的部分，用牛頓法增加解精度

有學過數值方法的讀者應該可以看得懂，因為整數演算法只是一個近似解，所以需要

用牛頓法 " 修飾 " 一下解，下面給出用牛頓法推導所得之疊代式。

 

圖 11. 用牛頓法導出求解疊代式

 

整個演算法核心的部分講完，下面給出一支帶有 GUI 介面的測試程式，並且稍微介紹一下

在下如何用 Tick 量測演算法所增進的效率。

 

圖 12. 兩種方法各執行 一百萬 次 用 GetTickCount

量測所經過的 Tick 數

 

 

從這支 GUI 測試可以發現，x86 CPU 是屬於 " 不穩定 " 的處理器，就是說要精確量測 x86

CPU 所經過的 cycle 數是不可能的事情，主要因為現在 x86 CPU 很複雜，內部有許多快取

預測的架構，所以同樣一支程式的執行時間會忽快忽慢，用這支程式就可以很明顯發現

這個現象，在 x86 平台上 Carmack 的快速反平方根演算法會比用標準數學程式庫算 

1/sqrt(x) 可能快 1.5x ~ 4x，x86 CPU 很聰明，假如曾經有計算過的某些數值，CPU 可能

直接使用快取內部的值，而不再重新計算，當然 CPU 內部實際怎麼做也許是難以理解

但是從測試結果表明，x86 CPU 並不是一種穩定的處理器，也許這個演算法可以拿到

別的平台試試看。

 

 

 

圖 13. 測試結果表明 雖然 x86 CPU 並非穩定的 CPU，但是

Carmack 的方法確實是異常的快，至少都有超過 1.5x 的速度

 

程式中的那個 Dial Widget 是 Qt 本身就有的 元件，用滾輪轉動 Dial Widget 可以動態的

觀察 speed 的變化，Carmack 的快速反平方根演算法來至少都有 1.5x 以上的速度

 

證明了為何這個演算法會被稱為

John Carmack's Unusual Fast Inverse Square Root

 

後記 : 這篇文章需要的材料比較多，主要的時間花在理解演算法的由來以及測試程式的撰寫

還有閱讀一些相關計算 平方根 與 反平方根相關的文獻閱讀，不過總算是寫成了。 

 

補充 : 現在 x86 裡面 SSE 指令集裡面就有 rsqrtss，讀者也可以利用這條指令獲得初始值

這條指令基本上就是 快速反平方根演算法 硬體化版本，一樣可以利用初始值做牛頓法疊代

增進解的精度，讀者有興趣可以自己試試看。

 

圖 14. 使用 SSE 指令 rsqrtss 計算反平方根，內插組合語言

分別給出了 CL 與 GCC 版本內插語法

 

讀者自己去測試就會知道，使用 rsqrtss 計算速度上並不會得到甚麼優勢，因為 SSE 指令內部

其實最後也是要使用 x86 內的浮點運算器，但是在語法上就變得很簡單，用 rsqrtss 可以直接

獲得近似解，用近似解做初始值放入牛頓法疊代增加解的精度。

 

對 x86 硬體結構不瞭解可以參考

Software Optimization Guide for the AMD64 Processors

Appendix A Microarchitecture for AMD Athlon 64 and AMD Opteron Processors

 

對 GCC 內插組合語言語法不熟又懶得看英文，可以參考

Linux Device Driver Programming 驅動程式設計 7-8 行內組譯