sam(后缀自动机)

后缀自动机ins解释

void ins(int c){
	int p=last;//将当前节点的parent节点变为last
	int np=++cnt;//建立新节点
	last=np;//将last设为当前节点
	l[np]=l[p]+1;//当前节点的长度为父节点+1
	for(;p&&!ch[p][c];p=fa[p])//若当前点的parent没有c这个儿子，则往上跳
	    ch[p][c]=np;//跳的过程中把这些点的c这个儿子设为当前节点
	if(!p)fa[np]=1;//若跳回到根，则parent为1
	else{
		int q=ch[p][c];//q为当前点的c这个儿子
		if(l[p]+1==l[q]){//若q的长度和p的长度相同，则不建立虚点
		    fa[np]=q;
		}else{
			int nq=++cnt;//建立新节点为虚点
			l[nq]=l[p]+1;//当前点的长度为他的parent的长度+1
			memcpy(ch[nq],ch[q],sizeof(ch[q]));//将这个原来点的信息复制到这个虚点上
			fa[nq]=fa[q];//虚点的parent为原节点的parent
			fa[q]=fa[np]=nq;//原节点和当前节点的parent都是虚点
			for(;ch[p][c];p=fa[p])//若当前点的parent没有c这个儿子，则往上跳
			    ch[p][c]=nq;//跳的过程中把这些点的c这个儿子设为当前节点
		}
	}
	size[np]=1;//用于反向拓扑
}

图片：

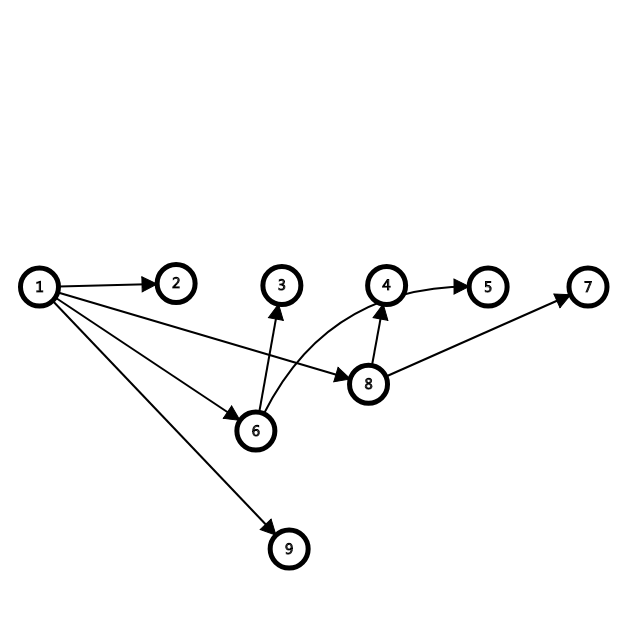
如字符串\(abcbcd\)

后缀自动机



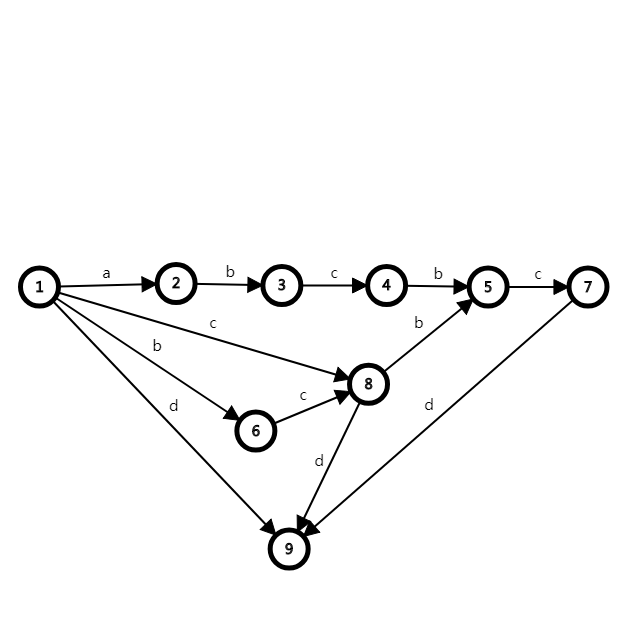
parent树