单因素方差分析（One Way ANOVA）

Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among group means in a sample. ANOVA was developed by statistician and evolutionary biologist Ronald Fisher.

什么是单因素方差分析

　　单因素方差分析是指对单因素试验结果进行分析，检验因素对试验结果有无显著性影响的方法。

　　单因素方差分析是两个样本平均数比较的引伸，它是用来检验多个平均数之间的差异，从而确定因素对试验结果有无显著性影响的一种统计方法。

单因素方差分析相关概念

因素：影响研究对象的某一指标、变量。
水平：因素变化的各种状态或因素变化所分的等级或组别。
单因素试验：考虑的因素只有一个的试验叫单因素试验。

单因素方差分析示例

　　例如，将抗生素注入人体会产生抗生素与血浆蛋白质结合的现象，以致减少了药效。下表列出了5种常用的抗生素注入到牛的体内时，抗生素与血浆蛋白质结合的百分比。现需要在显著性水平α = 0.05下检验这些百分比的均值有无显著的差异。设各总体服从正态分布，且方差相同。

青霉素	四环素	链霉素	红霉素	氯霉素
29.6	27.3	5.8	21.6	29.2
24.3	32.6	6.2	17.4	32.8
28.5	30.8	11.0	18.3	25.0
32.0	34.8	8.3	19.0	24.2

　　在这里，试验的指标是抗生素与血浆蛋白质结合的百分比，抗生素为因素，不同的5种抗生素就是这个因素的五个不同的水平。假定除抗生素这一因素外，其余的一切条件都相同。这就是单因素试验。试验的目的是要考察这些抗生素与血浆蛋白质结合的百分比的均值有无显著的差异。即考察抗生素这一因素对这些百分比有无显著影响。这就是一个典型的单因素试验的方差分析问题。

单因素方差分析的基本理论

　　与通常的统计推断问题一样，方差分析的任务也是先根据实际情况提出原假设H₀与备择假设H₁，然后寻找适当的检验统计量进行假设检验。本节将借用上面的实例来讨论单因素试验的方差分析问题。

　　在上例中，因素A（即抗生素）有s（=5）个水平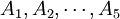，在每一个水平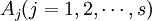下进行了n_j = 4次独立试验，得到如上表所示的结果。这些结果是一个随机变量。表中的数据可以看成来自s个不同总体（每个水平对应一个总体）的样本值，将各个总体的均值依次记为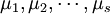,则按题意需检验假设

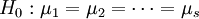
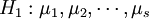　　不全相等

为了便于讨论，现在引入总平均μ

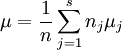　　其中：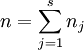

再引入水平A_j的效应δ_j

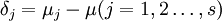
显然有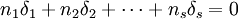，δ_j表示水平A_j下的总体平均值与总平均的差异。

利用这些记号，本例的假设就等价于假设

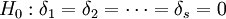
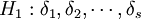　　不全为零

因此，单因素方差分析的任务就是检验s个总体的均值μ_j是否相等，也就等价于检验各水平A_j的效应δ_j是否都等于零。

　　2. 检验所需的统计量

　　假设各总体服从正态分布，且方差相同，即假定各个水平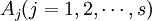下的样本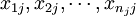来自正态总体N(μ_j,σ²)，μ_j与σ²未知，且设不同水平A_j下的样本之间相互独立，则单因素方差分析所需的检验统计量可以从总平方和的分解导出来。下面先引入：

　　水平A_j下的样本平均值:

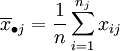
　　数据的总平均:

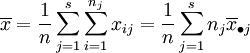
　　总平方和:

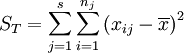
总平方和S_T反映了全部试验数据之间的差异，因此S_T又称为总变差。将其分解为

　　S_T = S_E + S_A

其中:

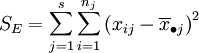
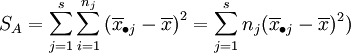
上述S_E的各项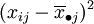表示了在水平A_j下，样本观察值与样本均值的差异，这是由随机误差所引起的，因此S_E叫做误差平方和。S_A的各项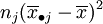表示了在水平A_j下的样本平均值与数据总平均的差异，这是由水平A_j以及随机误差所引起的，因此S_A叫做因素A的效应平方和。

　　可以证明S_A与S_E相互独立，且当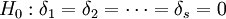为真时，S_A与S_E分别服从自由度为s − 1,n − s的χ²分布，即

　　S_A / σ²˜χ²(s − 1)

　　S_E / σ²˜χ²(n − s)

于是，当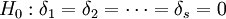为真时

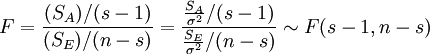
这就是单因素方差分析所需的服从F分布的检验统计量。

　　3. 假设检验的拒绝域

　　通过上面的分析可得，在显著性水平α下，本检验问题的拒绝域为

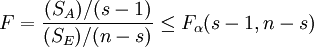
为了方便分析比较，通常将上述分析结果编排成如下表所示的方差分析表。表中的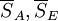分别称为S_A,S_E的均方。

方差来源	平方和	自由度	均方	F比
因素A	S_A	s − 1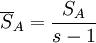
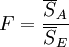误差	S_E	n − s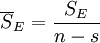
总和	S_T	n − 1

参考文献

赵丹亚，邵丽.中文版Excel2000应用案例.人民邮电出版社,2000年01月第1版