KL散度和交叉熵的对比介绍

KL散度（Kullback-Leibler Divergence）和交叉熵（Cross Entropy）是在机器学习中广泛使用的概念。这两者都用于比较两个概率分布之间的相似性，但在一些方面，它们也有所不同。本文将对KL散度和交叉熵的详细解释和比较。



KL散度和交叉熵

KL散度，也称为相对熵（Relative Entropy），是用来衡量两个概率分布之间的差异的一种度量方式。它衡量的是当用一个分布Q来拟合真实分布P时所需要的额外信息的平均量。KL散度的公式如下



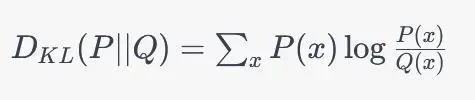
x是概率分布中的一个可能的事件或状态。P(x)和Q(x)分别表示真实概率分布和模型预测的概率分布中事件x的概率。

KL散度具有以下性质：

KL散度是非负的，即 KLD(P||Q) >= 0，当且仅当P和Q是完全相同的分布时等号成立。

KL散度不满足交换律，即 KLD(P||Q) != KLD(Q||P)。

KL散度通常不是对称的，即 KLD(P||Q) != KLD(Q||P)。

KL散度不是度量，因为它不具有对称性和三角不等式。

在机器学习中，KL散度通常用于比较两个概率分布之间的差异，例如在无监督学习中用于评估生成模型的性能。

交叉熵是另一种比较两个概率分布之间的相似性的方法。它的公式如下：



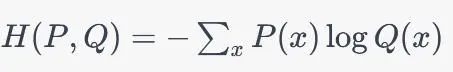
x是概率分布中的一个可能的事件或状态。P(x)和Q(x)分别表示真实概率分布和模型预测的概率分布中事件x的概率。交叉熵衡量了模型预测的概率分布与真实概率分布之间的差异，即模型在预测上的不确定性与真实情况的不确定性之间的差距。

与KL散度不同，交叉熵具有以下性质：

交叉熵是非负的，即CE(P, Q) >= 0，当且仅当P和Q是完全相同的分布时等号成立。

交叉熵满足交换律，即CE(P, Q) = CE(Q, P)。

交叉熵是对称的，即CE(P, Q) = CE(Q, P)。

交叉熵不是度量，因为它不具有三角不等式。

在机器学习中，交叉熵通常用于衡量模型预测和真实标签之间的差异。例如，在分类任务中，交叉熵被用作损失函数，以衡量模型预测的类别分布和真实标签之间的差。

KL散度与交叉熵的关系

L散度和交叉熵有一定的联系。在概率论中，KL散度可以被定义为两个概率分布之间的交叉熵与真实分布的熵的差值。具体地说，KL散度的公式如下



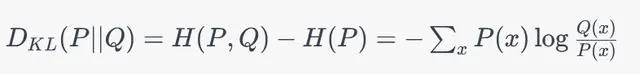
H(P, Q)表示P和Q的交叉熵，H(P)表示P的熵。可以看到，KL散度包含了交叉熵和熵的概念，因此它们之间有着密切的联系。

KL散度与交叉熵的应用

交叉熵通常用于监督学习任务中，如分类和回归等。在这些任务中，我们有一组输入样本和相应的标签。我们希望训练一个模型，使得模型能够将输入样本映射到正确的标签上。

在这种情况下，我们可以使用交叉熵作为损失函数。假设我们有一个模型预测的输出分布为p，真实标签的分布为q。那么交叉熵的公式如下



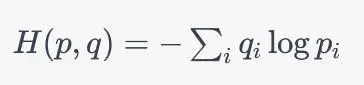
i表示可能的类别或事件，p_i和q_i分别表示真实概率分布和模型预测的概率分布中类别i的概率。

KL散度通常用于无监督学习任务中，如聚类、降维和生成模型等。在这些任务中，我们没有相应的标签信息，因此无法使用交叉熵来评估模型的性能，所以需要一种方法来衡量模型预测的分布和真实分布之间的差异，这时就可以使用KL散度来衡量模型预测的分布和真实分布之间的差异。KL散度的公式如下：



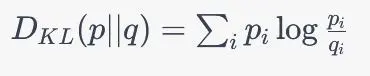
i表示概率分布中的一个可能的事件或状态。p_i和q_i分别表示真实概率分布和模型预测的概率分布中事件i的概率。KL散度衡量了模型预测的概率分布与真实概率分布之间的差异，即模型在预测上的不确定性与真实情况的不确定性之间的差距。

一般情况下：交叉熵通常用于监督学习任务中，KL散度通常用于无监督学习任务中。当我们有相应的标签信息时，应该使用交叉熵来评估模型的性能；当我们没有相应的标签信息时，使用KL散度可以衡量模型预测的分布和真实分布之间的差异。

总结

在本文中，我们介绍了KL散度和交叉熵这两个概念，并比较了它们之间的异同。KL散度用于比较两个概率分布之间的差异，而交叉熵用于衡量模型预测和真实标签之间的差异。尽管它们有一定的联系，但它们在使用和应用上还是有所区别。在机器学习中，KL散度和交叉熵都有着广泛的应用，可以用来评估模型的性能和更新模型参数。