LeetCode 332. Reconstruct Itinerary重新安排行程 (C++/Java)

题目：

Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.

Note:

1. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"].
2. All airports are represented by three capital letters (IATA code).
3. You may assume all tickets form at least one valid itinerary.

Example 1:

Input: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Output: ["JFK", "MUC", "LHR", "SFO", "SJC"]

Example 2:

Input: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Output: ["JFK","ATL","JFK","SFO","ATL","SFO"]
Explanation: Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"].
             But it is larger in lexical order.

分析：

给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 出发。

可以将题目理解为一个有向图，飞机票当成图的边，最后求的是结点的顺序，实际上是求一个欧拉回路。

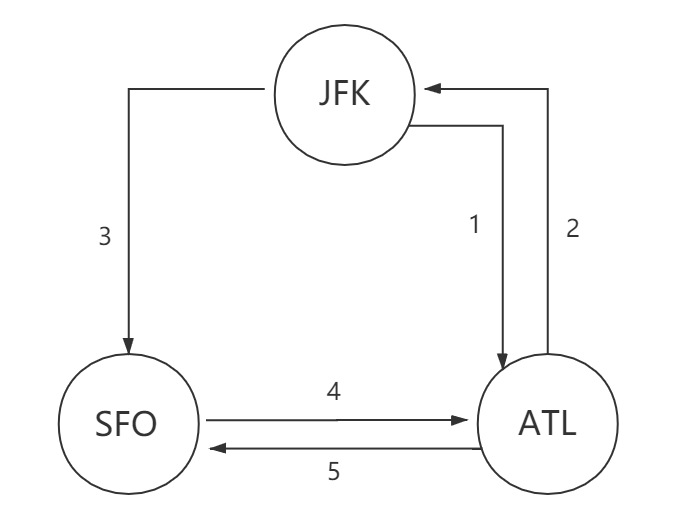
这里我们使用Hierholzer算法求解此问题。

正常来说我们应该先求出度为奇数的点，不过由于这道题告知要从“JFK”开始，所以我们可以直接从JFK开始搜索。

DFS(u):

　　while(u存在未被访问过的边e(u, v))

　　　　标记边e(u, v)已被访问

　　　　DFS(v)

　　END

　　将点u添加到路径集中

还是以上面的为例，从JFK开始，存在未被访问的边(1，3)，我们在这个选择3，也就是通往SFO的边(注意此题要求应该是选择字符排序小的点，这里只是模拟一下求解欧拉回路的过程)，然后我们将3这条边标记以访问。

然后从SFO开始，存在为被访问的边(4)，我们选择4这条边，到达了ATL这个点，同样的4也被标记访问过了。

ATL存在未被访问的边(5，2)，我们选择5这条边，到达了SFO这个点，5也被标记访问过。

SFO已经不存在未被访问的边了(4已经被标记访问过了)，所以我们将SFO加入到路径集中[SFO]，并返回上次访问的点。

此时ATL中还存在2这条边未被访问，我们选择2这条边，到达了JFK这个点，2也标记访问过。

JFK中1还未访问，我们选择1这条边，到达了ATL这个点，注意此时所有的边都已经访问过了，ATL没有边可以继续访问了，我们将ATL加入路径集[SFO，ATL]，返回上次访问的点。

此时JFK也没有边访问了，我们将JFK加入[SFO，ATL，JFK]

同理ATL也没有可访问的边了，将ATL加入[SFO，ATL，JFK，ATL]

返回到SFO，也没有边可以访问了，将SFO加入[SFO，ATL，JFK，ATL，SFO]

最后我们回到了出发点JFK，1，3都已被标记访问过，将JFK加入到路径集中得[SFO，ATL，JFK，ATL，SFO，JFK]，最后将结果集中数据反转一下即可得到所求得欧拉路径。也就是JFK->SFO->ATL->JFK->ATL->SFO

不过注意由于题中要求字符自然排序最小，所以我们在选择边时，要按照顺序选在下一个访问的结点。例如从JFK开始有通向SFO和ATL两个边，我们选择通往ATL的边，依照这样的规则我们可以得到结果

["JFK","ATL","JFK","SFO","ATL","SFO"]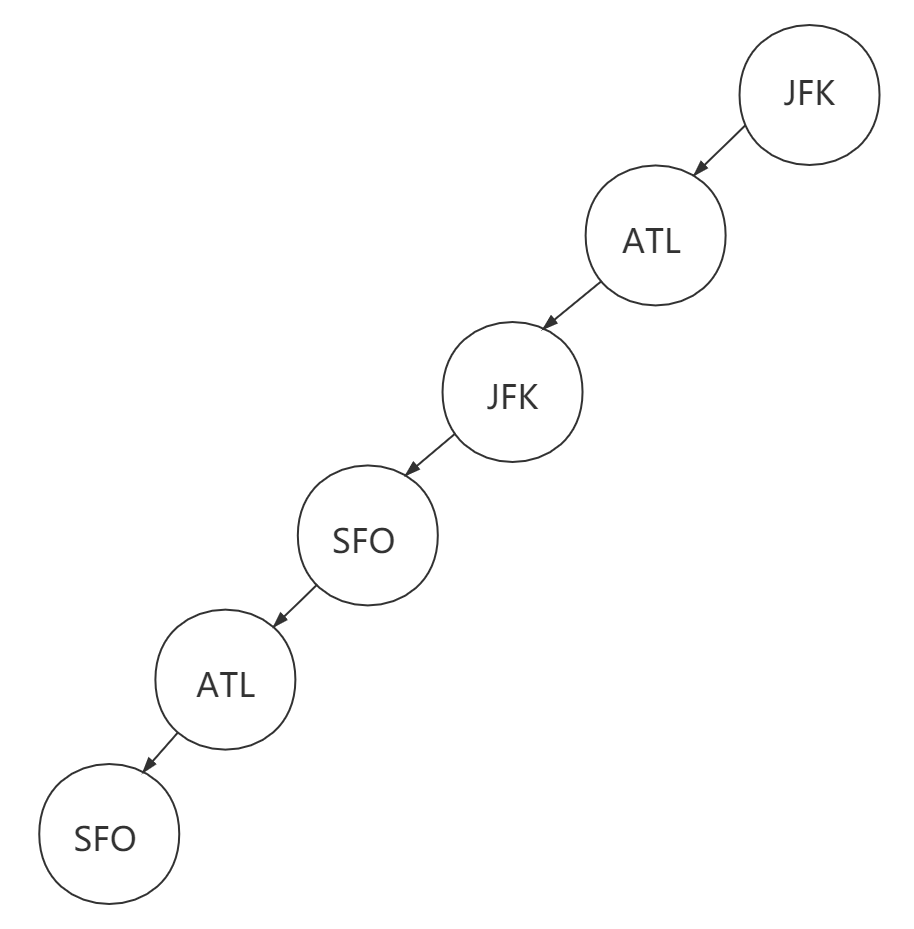

小技巧：在保存机票起点和终点时，我们可以使用有限队列存储边，优先访问字符小的边。

程序：

C++

class Solution {
public:
    vector<string> findItinerary(vector<vector<string>>& tickets) {
        for(int i = 0; i < tickets.size(); ++i){
            if(map.find(tickets[i][0]) == map.end()){
                priority_queue <string, vector<string>, cmp> q;
                q.push(tickets[i][1]);
                map[tickets[i][0]] = q;
            }
            else{
                map[tickets[i][0]].push(tickets[i][1]);
            }
        }
        findPath("JFK");
        reverse(res.begin(), res.end());
        return res;
    }
    void findPath(string begin){
        while(map.find(begin) != map.end() && map[begin].size() != 0){
            string next = map[begin].top();
            map[begin].pop();
            findPath(next);
        }
        res.push_back(begin);
    }
private:
    struct cmp
    {
        bool operator() (string a, string b)
        {
            return a > b;
        }
    };
    vector<string> res;
    unordered_map<string, priority_queue <string, vector<string>, cmp>> map;
};

Java

class Solution {
    public List<String> findItinerary(List<List<String>> tickets) {
        for(List<String> pair:tickets){
            String key = pair.get(0);
            String value = pair.get(1);
            if(!map.containsKey(key)){
                PriorityQueue<String> p = new PriorityQueue<>();
                p.add(value);
                map.put(key, p);
            }
            else{
                map.get(key).add(value);
            }
        }
        getPath("JFK");
        return res;
    }
    private void getPath(String begin){
        while(map.containsKey(begin) && map.get(begin).size() != 0){
            getPath(map.get(begin).poll());
        }
        res.add(0, begin);
    }
    private List<String> res = new ArrayList<>();
    private Map<String, PriorityQueue<String>> map = new HashMap<>();
}