CF916E 换根树上问题

Link

题意：对一棵树进行三种操作。

• 把根设为 \(x\)。
• 将以 \(lca(y, z)\) 为根的子树中所有点的权值加 \(v\)。
• 查询以 \(x\) 为根的子树点权之和。

初始根为 \(1\)。

设相对于当前 \(root\) 的所要操作（查询）子树的根节点为 \(U\)。

这里用 \([in[x], out[x]]\) 表示以 \(x\) 为根的子树在 \(dfs\) 序上的出现区间。

情况一：\(U = root\)。

修改整棵树。

情况二：直接在原树上修改子树 \(U\)。

满足以下条件之一：

• 整棵 \(U\) 在到 \(root\) 前已经遍历完了，\(out[U] < in[root]\)。
• 整棵 \(root\) 在到 \(U\) 前已经遍历完了，\(in[U] > out[root]\)。
• \(U\) 是 \(root\) 的后代，\(in[root] < in[U] < out[U] < out[root]]\)。

二三可以合写为 \(in[U] > in[root]\)。

情况三：\(root\) 为 \(U\) 的后代。

先整树修改，在扣除 \(U\) 在 \(root\) 方向的子树的影响。

如何求这个方向子树的根，可以借鉴 \(lca\) 的思想。

int get(int x, int y) {
	if(dep[x] < dep[y]) swap(x, y);
	per(i, 17, 0) if(dep[fa[x][i]] > dep[y]) x = fa[x][i];
	return x;
}

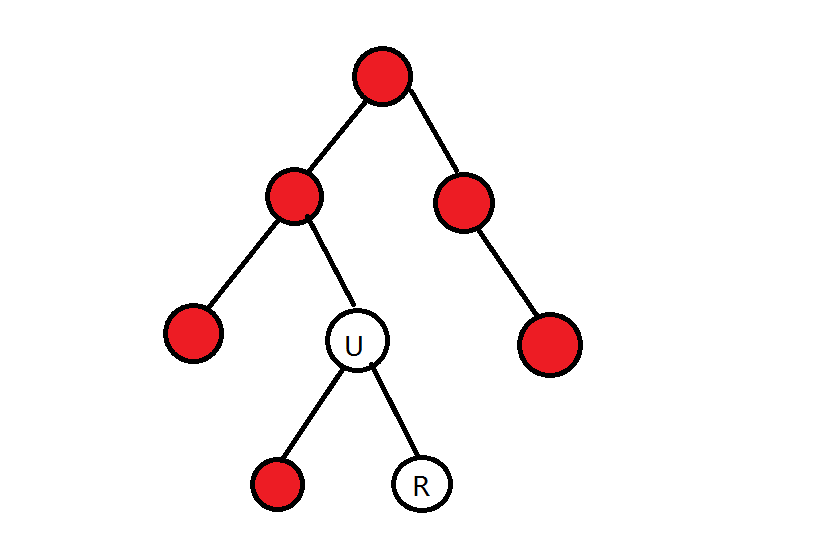
操作三的 \(U\) 就是 \(x\)。

对于操作二，\(U\) 为 \(lca(y, z)\)，\(lca(root, y)\)，\(lca(root, z\) 中深度最大的点，可以自己模拟一下。

int lca(int a, int b, int c) {
	int x = lca(a, b), y = lca(a, c);
	if(dep[x] < dep[y]) x = y;
	y = lca(b, c);
	if(dep[x] < dep[y]) x = y;
	return x;
}

具体做法就是线段树维护 \(dfs\) 序 + 大分讨，细节较多。

完整代码

#include<bits/stdc++.h>
#define rep(i, a, b) for(int i = (a); i <= (b); ++ i)
#define per(i, a, b) for(int i = (a); i >= (b); -- i)
#define pb emplace_back
#define All(X) X.begin(), X.end()
using namespace std;
using ll = long long;
constexpr int N = 1e5 + 5;

int n, m, dep[N], in[N], out[N], dfn;
int fa[N][18];
ll a[N];
vector<int> G[N];

struct Node {
	ll sum, tag;
	int sz;
} t[N << 2];

#define ls x << 1
#define rs ls | 1

void build(int x = 1, int l = 1, int r = n) {
	t[x].sz = r - l + 1;
	if(l == r) return;
	int mid = l + r >> 1;
	build(ls, l, mid), build(rs, mid + 1, r);
}

void pushup(int x) {
	t[x].sum = t[ls].sum + t[rs].sum;
}

void pushdown(int x) {
	if(t[x].tag) {
		t[ls].tag += t[x].tag, t[ls].sum += t[x].tag * t[ls].sz;
		t[rs].tag += t[x].tag, t[rs].sum += t[x].tag * t[rs].sz;
		t[x].tag = 0;
	}
}

void add(int L, int R, ll v, int x = 1, int l = 1, int r = n) {
	if(L > R) return;
	if(L <= l && r <= R) {
		t[x].sum += v * t[x].sz;
		t[x].tag += v;
		return;
	}
	pushdown(x);
	int mid = l + r >> 1;
	if(mid >= L) add(L, R, v, ls, l, mid);
	if(mid < R) add(L, R, v, rs, mid + 1, r);
	pushup(x);
}

ll query(int L, int R, int x = 1, int l = 1, int r = n) {
	if(L > R) return 0;
	if(L <= l && r <= R) {
		return t[x].sum;
	}
	pushdown(x);
	int mid = l + r >> 1;
	ll ret = 0;
	if(mid >= L) ret += query(L, R, ls, l, mid);
	if(mid < R) ret += query(L, R, rs, mid + 1, r);
	return ret;
}

void dfs(int x) {
	dep[x] = dep[fa[x][0]] + 1;
	in[x] = ++ dfn;
	add(dfn, dfn, a[x]);

	for(auto y : G[x]) {
		if(y != fa[x][0]) {
			fa[y][0] = x;
			rep(i, 1, 17) fa[y][i] = fa[fa[y][i - 1]][i - 1];
			dfs(y);
		}
	}
	out[x] = dfn;
}

int lca(int x, int y) {
	if(dep[x] < dep[y]) swap(x, y);
	per(i, 17, 0) if(dep[fa[x][i]] >= dep[y] ) x = fa[x][i];
	if(x == y) return x;
	per(i, 17, 0) if(fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
	return fa[x][0];
}
int lca(int a, int b, int c) {
	int x = lca(a, b), y = lca(a, c);
	if(dep[x] < dep[y]) x = y;
	y = lca(b, c);
	if(dep[x] < dep[y]) x = y;
	return x;
}
int get(int x, int y) {
	if(dep[x] < dep[y]) swap(x, y);
	per(i, 17, 0) if(dep[fa[x][i]] > dep[y]) x = fa[x][i];
	return x;
}

int root = 1;

int main() {
	ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
	cin >> n >> m;
	rep(i, 1, n) cin >> a[i];
	rep(i, 2, n) {
		int x, y; cin >> x >> y;
		G[x].pb(y);
		G[y].pb(x);
	}
	build(), dfs(1);
	rep(i, 1, m) {
		int op; cin >> op;
		if(op == 1) {
			cin >> root;
		}
		if(op == 2) {
			int y, z, v; cin >> y >> z >> v;
			int x = lca(root, y, z);

			if(x == root) {
				add(1, n, v);
			}
			else {
				if(in[x] > in[root] || out[x] < in[root]) {
					add(in[x], out[x], v);
				}
				else {
					int Fa = get(x, root);
					add(1, n, v);
					add(in[Fa], out[Fa], -v);
				}
			}
		}
		if(op == 3) {
			int x; cin >> x;
			if(x == root) {
				cout << t[1].sum << '\n';
			}
			else {
				if(in[x] > in[root] || out[x] < in[root]) {
					cout << query(in[x], out[x]) << '\n';
				}
				else {
					int Fa = get(x, root);
					cout << t[1].sum - query(in[Fa], out[Fa]) << '\n';
				}
			}
		}
	}
	return 0;
}