bzoj2038小z的袜子

用平面曼哈顿距离最小生成树或者莫队算法都可以吖QwQ~

然而显然后者更好写（逃~）

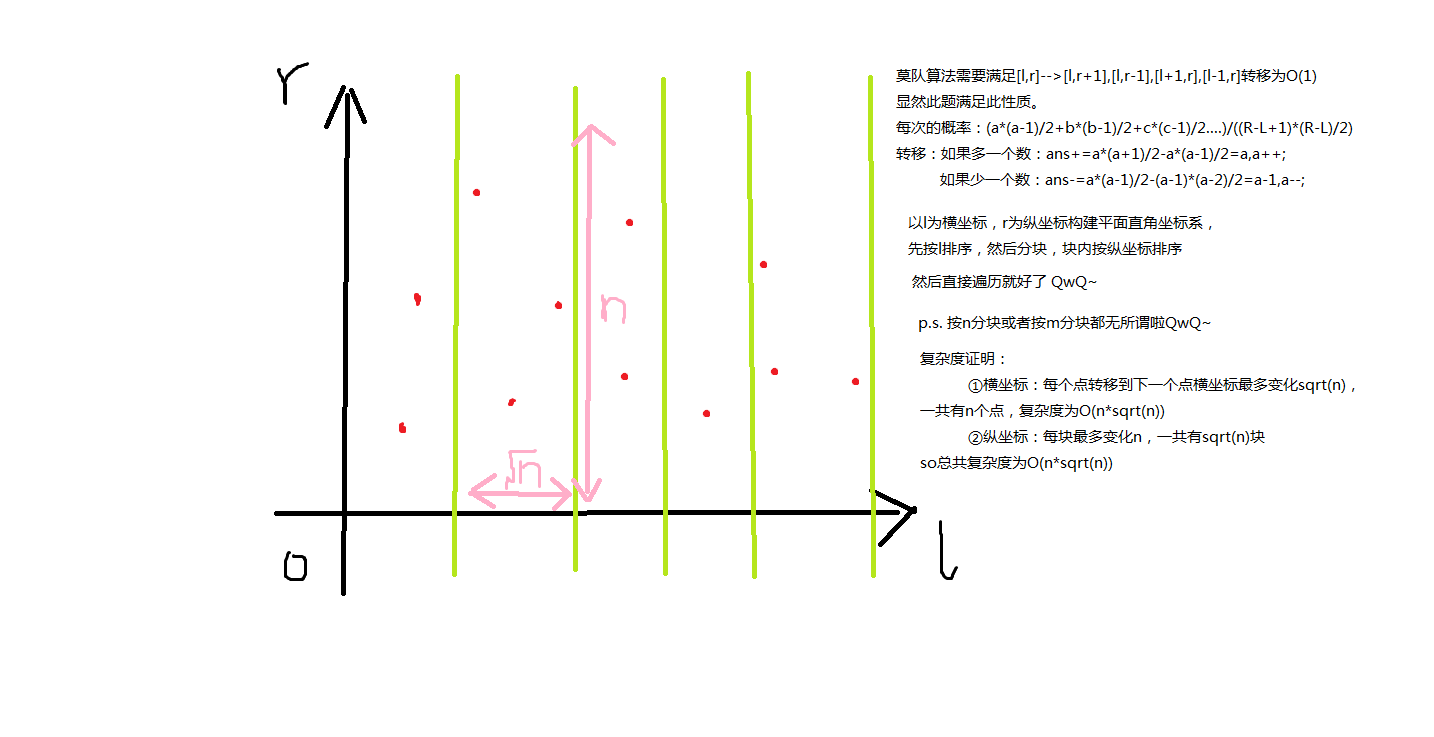
莫队怎么写就看图吧QwQ~

话说我一开始没开long long然后拍了3000组没拍出错交上去Wa了QAQ

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#define int long long
using namespace std;
const int Mx=;
struct Node { int l,r,num; } que[Mx];
bool cmp1 (Node a,Node b) { return a.l<b.l; }
bool cmp2 (Node a,Node b) { return a.r<b.r; }
int n,m,c[Mx],num[Mx],ans[Mx],ans1[Mx][];
inline int gcd (int a,int b) { int tmp; while(a>) tmp=b%a,b=a,a=tmp;  return b; }
signed main()
{
    scanf("%lld%lld",&n,&m);
    for(int i=;i<=n;i++) scanf("%lld",&c[i]);
    for(int i=;i<=m;i++) { scanf("%lld%lld",&que[i].l,&que[i].r);if(que[i].l>que[i].r) swap(que[i].l,que[i].r); }
    for(int i=;i<=m;i++) que[i].num=i;
    sort(que+,que++m,cmp1);
    for(int i=;i<=m;i+=sqrt(m)) sort(que+i,que+min(m,i+(int)sqrt(m)),cmp2);
    for(int i=;i<=m;i++)
    {
        if(i%(int)sqrt(m)==||i==)
        {
            memset(num,,sizeof(num));
            for(int j=que[i].l;j<=que[i].r;j++) num[c[j]]++;
            for(int j=;j<=n;j++) ans[i]+=num[j]*(num[j]-)/;
        }
        else
        {
            for(int j=que[i-].l,to=que[i].l;j!=to;)
            {
                if(j<to) ans[i]-=num[c[j]]-,num[c[j]]--,j++;
                else ans[i]+=num[c[j-]],num[c[j-]]++,j--;
            }
            for(int j=que[i-].r,to=que[i].r;j!=to;)
            {
                if(j<to) ans[i]+=num[c[j+]],num[c[j+]]++,j++;
                else ans[i]-=num[c[j]]-,num[c[j]]--,j--;
            }
            ans[i]+=ans[i-];
        }
        int div=gcd(ans[i],(que[i].r-que[i].l+)*(que[i].r-que[i].l)/);
        if(que[i].r==que[i].l||ans[i]==) ans1[que[i].num][]=,ans1[que[i].num][]=;
        else ans1[que[i].num][]=ans[i]/div,ans1[que[i].num][]=(que[i].r-que[i].l+)*(que[i].r-que[i].l)/(div*);
    }
    for(int i=;i<=m;i++) printf("%lld/%lld\n",ans1[i][],ans1[i][]);
    return ;
}