Nhk R1 Editorial

前言

这场比赛的锅貌似有点多…在准备的时候就已经推迟过三次，在这里为对各位比赛时造成的困扰抱歉。这是出题组第一次放比赛，欢迎批评指正。

主要问题在于 C 的数据造水了，hack 数据造反了于是没有 hack 到。D 的数据也不强。再次感到抱歉，并且努力做出改正。

最后重拾一下出比赛的初心以及发表一些 mozheng & Chuni 言论：罚金一百万元（不是），以及为自己的 Welcome to NHK 做一个 Sunny Side 式的收尾，或者称之为小结。总之都没差啦……虽然只是举个例子，但我们要告诉你的，就是这样的故事。

Oops!

A

给出两种构造方式：

• 考虑 \(d\) 的每一位，如果当前位为 \(0\)，则不对答案产生影响；如果当前位为 \(1\)，又因为 \(1\text{ xor }1\text{ xor }0=0,1\text{ or }1\text{ or }0=1\)，所以把 \(a,b,c\) 其中两个按位或上 \(2^i\) 即可。
• \(\begin{cases}a=d\\b=\text{lowbit}(d)\\c=d\text{ xor }\text{lowbit}(d)\end{cases}\)

当然这两种方式并无什么不同。无解的情况是 \(d=2^n\)。

#include<bits/stdc++.h>
int ans[3],d;
signed main() {
	scanf("%d",&d);
	if((d&-d)==d)	return puts("-1"),0;
	for(int now=0; d; d^=d&-d)	ans[now]|=d&-d,ans[(now+=1)%=3]|=d&-d;
	printf("%d %d %d\n",ans[0],ans[1],ans[2]);
	return 0;
}

#include<bits/stdc++.h>
int d;
signed main() {
	scanf("%d",&d);
	if((d&-d)==d)	return puts("-1"),0;
	printf("%d %d %d\n",d,(d&-d),d-(d&-d));
	return 0;
}

B

首先 \(a_1=x_1\)，考虑第二位，因为保证有解，所以 \(x_2\mid x_1\)，同理可得 \(\forall i\in(1,n],x_i\mid x_{i-1}\)，可以预见数据中最多有 \(\log\) 个非 \(1\) 数，于是不断往上推即可。

#include<bits/stdc++.h>
int n,x,pre,now,vis[2000100];
signed main() {
	scanf("%d\n%d",&n,&x);
	vis[pre=now=x]=1;
	printf("%d ",x);
	for(int i=1; i<n; ++i) {
		scanf("%d",&x);
		if(pre!=x)	pre=now=x;
		else	while(vis[now])	now+=pre;
		vis[now]=1;
		printf("%d ",now);
	}
	return 0;
}

C

首先我们有个 \(\mathcal {O}(nm)\) 的暴力遍历做法，读者很容易想到这样遍历了太多冗余的点。

于是很自然地想到将一个块缩成一个点。具体的，对于每一列，我们将障碍物隔开的一列点看成一个点，这样的店最多有 \(2k\) 个。

然后 dp 即可，\(dp_i=[(\sum_{j=1}^idp_j)>0]\)。

然后要注意一个块能否转移到另一个块的判断条件有细节：并不是看两个块是联通，而是定义 \(mx_i\) 为能到达第 \(i\) 个块的最低点（贪心），看从 \(mx_j\) 起是否能到达 \(mx_i\)，再更新 \(mx_i\)。

当然好像有更简便的做法，余不会。

同时存在更优的做法，为了代码的简便起见并没有作为 std，欢迎分享。

#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <vector>
#include <map>
#define LL long long
#define Min(x,y) ((x)<(y)?(x):(y))
#define Max(x,y) ((x)>(y)?(x):(y))
using namespace std;
const int MAXN = 5005, MAXM = 1e7 + 5;
vector <int> v[MAXM], cx;
map <int, bool> vis;
map <int, int> lst;
struct Point {
	int X, Y, Y_;
}arr[MAXN];
int n, m, k, tot, mx, mn[MAXN];
int pre[MAXM];
bool dp[MAXN];
bool check(int x, int y) {
	if(arr[x].X == arr[y].X - 1) {
		if(arr[x].Y_ < arr[y].Y) return 0;
		if(arr[x].Y > arr[y].Y_) return 0;
		if(max(arr[y].Y, mn[x]) >= arr[y].Y && max(arr[y].Y, mn[x]) <= arr[y].Y_) {
			mn[y] = min(mn[y], max(arr[y].Y, mn[x])); return 1;
		}
		return 0;
	}
	if(arr[x].Y > arr[y].Y_) return 0;
	if(max(arr[y].Y, mn[x]) >= arr[y].Y && max(arr[y].Y, mn[x]) <= arr[y].Y_) {
		mn[y] = min(mn[y], max(arr[y].Y, mn[x])); return 1;
	}
	return  0;
}
int main() {
	int x, y;
	scanf("%d%d%d", &n, &m, &k); memset(mn, 0x3f, sizeof(mn));
	for(int i = 1; i <= k; i ++) {
		scanf("%d%d", &x, &y); v[x].push_back(y); cx.push_back(x); mx = max(mx, x);
	}
	sort(cx.begin(), cx.end());
	int Lst = 0;
	for(auto i : cx) {
		if(vis[i]) continue;
		pre[i] = 1;
		lst[i] = Lst; Lst = i; sort(v[i].begin(), v[i].end()); vis[i] = 1;
		int las = 0;
		for(auto j : v[i]) {
			if(j == las) { las ++; continue; }
			tot ++; arr[tot].X = i; arr[tot].Y = las; arr[tot].Y_ = j - 1; las = j + 1;
		}
		if(las <= m) tot ++, arr[tot].X = i, arr[tot].Y = las, arr[tot].Y_ = m;
	}
	for(int i = 1; i <= 10000000; i ++) pre[i] += pre[i - 1];
//	for(int i = 1; i <= tot; i ++) {
//		printf("%d %d %d\n", arr[i].X, arr[i].Y, arr[i].Y_);
//	}
	if(!tot) { printf("Yes"); return 0; }
	if(vis[0]) {
		if(arr[1].Y != 0) { printf("No"); return 0; }
		dp[1] = 1; mn[1] = 0;
	}
	else {
		for(int i = 1; i <= tot; i ++) if(arr[i].X == arr[1].X) dp[i] = 1, mn[i] = arr[i].Y, dp[i] = 1;
	}
	for(int i = 1; i <= tot; i ++) {
		for(int j = 1; j < i; j ++) {
			if(arr[j].X == arr[i].X) continue;
			if(((arr[j].X + 1 < arr[i].X && pre[arr[i].X - 1] - pre[arr[j].X] == 0) || arr[j].X + 1 == arr[i].X) && arr[j].X == lst[arr[i].X] && check(j, i)) {
				dp[i] |= dp[j];
			}
		}
	}
	if(vis[n]) {
		if(arr[tot].Y_ != m) { printf("No"); return 0; }
		if(dp[tot]) printf("Yes");
		else printf("No");
	}
	else {
		bool ans = 0;
		for(int i = 1; i <= tot; i ++) if(arr[i].X == mx) ans |= dp[i];
		if(ans) printf("Yes");
		else printf("No");
	}
	return 0;
}

D

你考虑维护 \(n\) 个单调队列。第 \(i\) 个单调队列的数满足：\(\sum_{d=1}^ia_dc_d\)，其中 \(c_i\) 一定为正数。

每次我们取 \(n\) 个单调队列的队头最小值 \(r\)，设其在第 \(i\) 个队列，那么我们将 \(a_d+r\) 放入第 \(d\) 个队列中。（\(i<d\le n\)）

可以证明，由于 \(a\) 数组为正数，这样队列一定是单调的。

一直这样做 \(k\) 次，取 \(r_k\) 即可。时间复杂度：\(\mathcal {O}(nk)\)。数据可以（？）把带 \(\mathrm {log}\) 做法卡掉。

#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <ctime>
#include <queue>
#define LL long long
using namespace std;
const int MAXN = 85;
queue <LL> que[MAXN];
int n, k, a[MAXN], num;
LL minn;
int main() {
	scanf("%d%d", &n, &k); k --;
	for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);
	que[0].push(0);
	for(int i = 1; i <= k + 1; i ++) {
		minn = 9e18;
		for(int j = 0; j <= n; j ++) if(!que[j].empty() && que[j].front() < minn) minn = que[j].front(), num = j;
        while(que[0].size()) que[0].pop();
		que[num].pop();
		for(int j = num; j <= n; j ++) que[j].push(minn + a[j]);
	}
	printf("%lld", minn);
	return 0;
}

E

\(f_i(\Delta)\) 表示第 \(v_i\) 这个点在坐标加 \(\Delta\) 时距离自己最近的 \(c\) 点的距离。那么这个画出来就是一条折线，由若干条斜率为 \(1\) 或 \(-1\) 的直线拼接而成。再设 \(F(\Delta)=\sum\limits_{i=1}^{b}f_i(\Delta)\)，也就是取 \(\Delta\) 时，题面中要求的距离之和。

在折线的拐点上研究，设 \(\textbf{G}_i\) 为 \(f_i(\Delta)\) 图像上所有拐点的集合，再设 \(\textbf{G}'=\bigcup\limits_{i=1}^{b}\textbf{G}_i\)。w.l.o.g，提出两个数 \(a,b,s.t.(a,f(a)),(b,f(b))\in\textbf{G}'\)，且不存在 \(c,s.t.(c,f(c))\in\textbf{G}',c-a>0,b-c>0\)，即 \(a,b\) 是紧相邻的。换而言之，就是把所有 \(v\) 点的图像拼在一起，取两个相邻的 \(a,b\) 拐点来研究。

现在我们可以求出 \(F(a)\)，以及拐点后的直线斜率，从而可以求出 \(F(b)\)。以此，扫一遍就行了。

我们举个例子来画图：

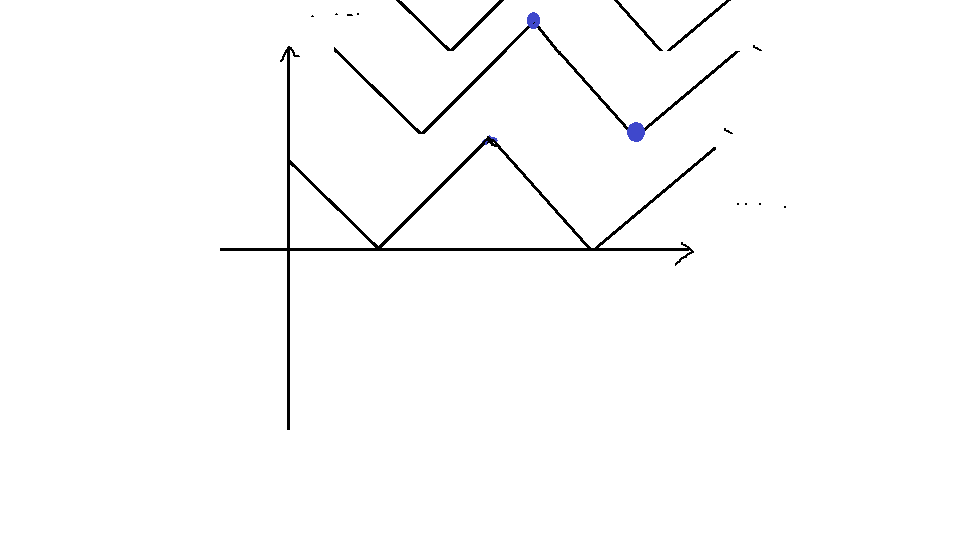
这个就是 \(f(\Delta)\) 的图像（我把多个 \(i\) 的拼在一起的）。现在假设我们取的 \(a,b\) 两点就是图中的蓝点（当然，\(a,b\) 之间没有其他拐点，因为 \(a,b\) 是紧相邻的），这意味着我确定了 \(a\) 点处的 \(\Delta\)，那么就可以算出 \(F(a)\) 了，如此往后面扫，每次取最大值就行了。

/*
每个点处在每个区间的值是不相同的，但是是一个折线。
当它在[vi,vi+1]中间时，如果靠vi更近，则为与vi的距离，否则为与vi+1的距离。
那我们现在知道了每个点移动多少之后的答案。
这条折线有的地方是斜率-1，有的地方是斜率为+1.
那么我们把所有的折线加在一起。一共有ab个点，我们维护一下每一段的斜率，然后求下最大值就好…… 

1 1 1
0
0

4
10
3
0 0 1 1 3 3 3 3 4 4
0 1 4

13 2 9
2 9
0 1 2 3 5 6 7 11 12
*/
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
vector<long long> pri;
const long long INF=1e18;
long long l,n,m,a[1010],b[1010],delup,deldown,sols[4000010],cur,ans,s,mxs;
double mxp;
struct line
{
	long long l,r,num;
}lin[2000010];
long long nothingtimes;
void donothing()
{
	++nothingtimes;
}
long long ABS(long long x)
{
	return x>=0?x:-x;
}
long long lint;
int main()
{
	scanf("%lld %lld %lld",&l,&n,&m);
	for(long long i=1;i<=n;++i)	scanf("%lld",&a[i]);
	for(long long i=1;i<=m;++i)	scanf("%lld",&b[i]);
	deldown=0;
	delup=l-b[m];
	deldown<<=1;
	delup<<=1;
	for(long long i=1;i<=n;++i)//第i个目标点
	{
		for(long long j=1;j<m;++j)//位于第j个与第j+1个点之间 距离都*2了，因为中点可能不在格点上。
		{
			//靠左
			long long l=a[i]*2-(b[j]+b[j+1]),r=(a[i]-b[j])*2;
			if(l>delup||r<deldown||l>=r)	donothing();
			else
			{
				if(l<deldown)	l=deldown;
				if(r>delup)	r=delup;
				if(l>=r)	donothing();
				else
				{
					lin[++lint].l=l;
					lin[lint].r=r;
					lin[lint].num=-1;
				}
			}
			//靠右
			l=a[i]*2-b[j+1]*2,r=a[i]*2-(b[j]+b[j+1]);
			if(l>delup||r<deldown||l>=r)	donothing();
			else
			{
				if(l<deldown)	l=deldown;
				if(r>delup)	r=delup;
				if(l>=r)	donothing();
				else
				{
					lin[++lint].l=l;
					lin[lint].r=r;
					lin[lint].num=1;
				}
			}
		}
		//在第1个前面
		long long l=a[i]*2-b[1]*2,r=delup;
		if(l>delup||r<deldown||l>=r)	donothing();
		else
		{
			if(l<deldown)	l=deldown;
			if(r>delup)	r=delup;
			if(l>=r)	donothing();
			else
			{
				lin[++lint].l=l;
				lin[lint].r=r;
				lin[lint].num=1;
			}
		}
		//在第n个后面
		l=deldown,r=a[i]*2-b[m]*2;
		if(l>delup||r<deldown||l>=r)	donothing();
		else
		{
			if(l<deldown)	l=deldown;
			if(r>delup)	r=delup;
			if(l>=r)	donothing();
			else
			{
				lin[++lint].l=l;
				lin[lint].r=r;
				lin[lint].num=-1;
			}
		}
	}
	for(long long i=1;i<=lint;++i)
	{
		pri.push_back(lin[i].l);
		pri.push_back(lin[i].r);
	}
	sort(pri.begin(),pri.end());
	pri.erase(unique(pri.begin(),pri.end()),pri.end());
	s=pri.size();
	for(long long i=1;i<=lint;++i)
	{
		lin[i].l=lower_bound(pri.begin(),pri.end(),lin[i].l)-pri.begin()+1;
		lin[i].r=lower_bound(pri.begin(),pri.end(),lin[i].r)-pri.begin()+1;
	}
	for(long long i=1;i<=lint;++i)
	{
		sols[lin[i].l]+=lin[i].num;
		sols[lin[i].r]-=lin[i].num;
	}
	mxp=-1;
	mxs=-1;
	for(long long i=1;i<=n;++i)
	{
		long long nowpos=a[i]*2+deldown,minn=INF;
		for(long long j=1;j<=m;++j)	minn=min(minn,ABS(nowpos-b[j]*2));
		cur+=minn;
	}
	if(cur<=l*2)
	{
		mxp=deldown;
		mxs=cur;
	}
	for(long long i=1;i<=s;++i)	sols[i]+=sols[i-1];
	for(long long i=1;i<s;++i)
	{
		if(cur>l*2)
		{
			long long tmp=cur+sols[i]*(pri[i]-pri[i-1]);
			if(tmp<=l*2)
			{
				mxs=l*2;
				mxp=(l*2-cur)*1.0/sols[i]+pri[i-1];
			}
			cur=tmp;
		}
		else
		{
			long long tmp=cur+sols[i]*(pri[i]-pri[i-1]);
			if(tmp<=l*2)
			{
				if(tmp>=mxs)
				{
					mxp=pri[i];
					mxs=tmp;
				}
			}
			else
			{
				mxp=(l*2-cur)*1.0/sols[i]+pri[i-1];
				mxs=l*2;
			}
			cur=tmp;
		}
	}
	if(mxp==-1)	printf("NO\n");
	else	printf("%.6lf\n",mxp/2);
	return 0;
}

F

首先我们定义 \(sec(i)\) 表示包含 \(0 \sim i-1\) 的最小区间。因为添加新的元素不会使区间变小， 所以 \(sec(i) \subseteq sec(i + 1)\) ，因此对于每个包含 \(sec(i)\) 的区间， 它肯定是包含 \(sec(1\sim i)\) 。若这个区间并不包含 \(sec(i + 1)\) ， 则也可以得到这个区间不包含 \(sec(i + 1 \sim n)\) 所以， 这个区间的贡献应该是 \(i\) 。

将这 \(i\) 的贡献分别分到 \(sec(1 \sim i)\) 中， 我们的问题就变成了， 每一次添加元素后， \(\large\sum \limits_{j= 1}^{i}\) 包含 \(sec(j)\) 的区间个数。考虑一次插入后答案的变化，同时规定 \(sec(0) = \varnothing\)：

一次插入的数 \(x\) 一定满足 \(\exists y \in [0, i - 1], x \in sec(y), x \notin sec(y + 1)\) 。而这个 \(y\) 是唯一的（这个应该很好想吧）。

所以， 我们可以预处理出每一个 \(x\) 对应的 \(y\) 。当插入 \(x\) 的时候， 相当于在所有 \(sec(1 \sim y)\) 的左（或右）边增加了 \(1\) 个点。

此时增加的区间数量即是 \(sec(1 \sim y)\) 右（或左）边的点个数之和（注意， 对于一个点是可以重复计算的）， 这里只需要用两个线段树分别记录 \(sec(i)\) 左右当前各有多少点了。

Bonus：Solve it in \(O(n)\)！

#include <cstdio>
#include <algorithm>
using namespace std;

#define MAXN 1000000
#define L(p) (p << 1)
#define R(p) ((p << 1) | 1)
#define make_mid(l,r) int mid = (l + r) >> 1

int s[MAXN + 5];
pair <int, int> si[MAXN + 5];
int sl[MAXN + 5], sr[MAXN + 5];
struct node {
	long long v;
	long long sign;
	int h, t;
}s1[(MAXN << 4) + 5], s2[(MAXN << 4) + 5];

void build (int p, int l, int r) {
	s1[p].h = l;
	s1[p].t = r;
	s1[p].sign = 0;
	s1[p].v = 0;
	s2[p].h = l;
	s2[p].t = r;
	s2[p].sign = 0;
	s2[p].v = 0;
	if (l == r) {
		return ;
	}
	make_mid (l, r);
	build (L(p), l, mid);
	build (R(p), mid + 1, r);
}
void downloadl (int p) {
	if (s1[p].sign && s1[p].h < s1[p].t) {
		s1[L(p)].sign += s1[p].sign;
		s1[R(p)].sign += s1[p].sign;
		s1[L(p)].v += (s1[L(p)].t - s1[L(p)].h + 1) * s1[p].sign;
		s1[R(p)].v += (s1[R(p)].t - s1[R(p)].h + 1) * s1[p].sign;
		s1[p].sign = 0;
	}
}
void downloadr (int p) {
	if (s2[p].sign && s2[p].h < s2[p].t) {
		s2[L(p)].sign += s2[p].sign;
		s2[R(p)].sign += s2[p].sign;
		s2[L(p)].v += (s2[L(p)].t - s2[L(p)].h + 1) * s2[p].sign;
		s2[R(p)].v += (s2[R(p)].t - s2[R(p)].h + 1) * s2[p].sign;
		s2[p].sign = 0;
	}
}
void changel (int p, int l, int r, long long x) {
	downloadl (p);
	if (s1[p].h >= l && s1[p].t <= r) {
		s1[p].v += x * (s1[p].t - s1[p].h + 1);
		s1[p].sign += x;

		return ;
	}
	make_mid (s1[p].h, s1[p].t);
	if (l <= mid) {
		changel (L(p), l, r, x);
	}
	if (r > mid) {
		changel (R(p), l, r, x);
	}
	s1[p].v = s1[L(p)].v + s1[R(p)].v;
}
void changer (int p, int l, int r, long long x) {
	downloadr (p);
	if (s2[p].h >= l && s2[p].t <= r) {
		s2[p].v += x * (s2[p].t - s2[p].h + 1);
		s2[p].sign += x;

		return ;
	}
	make_mid (s2[p].h, s2[p].t);
	if (l <= mid) {
		changer (L(p), l, r, x);
	}
	if (r > mid) {
		changer (R(p), l, r, x);
	}
	s2[p].v = s2[L(p)].v + s2[R(p)].v;
}
long long Suml (int p, int l, int r) {
	downloadl (p);
	if (s1[p].h >= l && s1[p].t <= r) {
		return s1[p].v;
	}

	long long sum = 0;

	make_mid (s1[p].h, s1[p].t);
	if (l <= mid) {
		sum += Suml (L(p), l, r);
	}
	if (r > mid) {
		sum += Suml (R(p), l, r);
	}

	return sum;
}
long long Sumr (int p, int l, int r) {
	downloadr (p);
	if (s2[p].h >= l && s2[p].t <= r) {
		return s2[p].v;
	}

	long long sum = 0;

	make_mid (s2[p].h, s2[p].t);
	if (l <= mid) {
		sum += Sumr (L(p), l, r);
	}
	if (r > mid) {
		sum += Sumr (R(p), l, r);
	}

	return sum;
}

int main () {
	int n;

	scanf ("%d", &n);
	for (int i = 1; i <= n; i ++) {
		int x;

		scanf ("%d", &x);
		s[x + 1] = i;//处理出i插入到的是哪个位置
	}
	build (1, 1, n);//初始两棵线段树
    //初始 sec(i)
    //----------------------------------------------
	si[1].first = s[1];
	si[1].second = s[1];
	for (int i = 2; i <= n; i ++) {
		si[i].first = min (si[i - 1].first, s[i]);
		si[i].second = max (si[i - 1].second, s[i]);
	}
    //----------------------------------------------
    //处理出 i 所对应的 y 且处理出到底是在 sec(y) 的左还是右
	for (int i = n - 1; i >= 1; i --) {
		for (int j = si[i + 1].first; j < si[i].first; j ++) {
			sr[j] = i;
		}
		for (int j = si[i + 1].second; j > si[i].second; j --) {
			sl[j] = i;
		}
	}

	long long ans = 0;//保存每次插入的答案
	long long Ans = 0;//保存最终答案

	for (int i = 1; i <= n; i ++) {
		if (sl[s[i]]) {
			ans += Suml (1, 1, sl[s[i]]);
			changer (1, 1, sl[s[i]], 1);
		}
		if (sr[s[i]]) {
			ans += Sumr (1, 1, sr[s[i]]);
			changel (1, 1, sr[s[i]], 1);
		}
		ans ++;//添加了 i 以后会多出 sec() ， 此处将其加入答案中
		changel (1, i, i, 1);
		changer (1, i, i, 1);
		Ans += ans;
	}
	printf ("%lld", Ans);
}

For some reason...

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define cmin(x, y) x = min(x, y)
#define cmax(x, y) x = max(x, y)
template<typename T=int> T read() {
	T x=0; char IO=getchar(); bool f=0;
	while(IO<'0' || IO>'9')	f|=IO=='-',IO=getchar();
	while(IO>='0' && IO<='9')	x=x*10+(IO&15),IO=getchar();
	return f?-x:x;
}
int n, a[1000100], mn[1000100], mx[1000100], pos1[1000100], pos2[1000100];
ll ans, _ans;
struct segment_tree {
	ll sum[4000100], tag[4000100];
	void up(const int now) {sum[now] = sum[now<<1]+sum[now<<1|1];}
	void down(const int now, int l, int r) {
		if(!tag[now]) return;
		int mid = (l+r)>>1;
		tag[now<<1] += tag[now],tag[now<<1|1] += tag[now];
		sum[now<<1] += (mid-l+1)*tag[now],sum[now<<1|1] += (r-mid)*tag[now];
		tag[now] = 0;
	}
	void go(int x, int y, ll k, const int now=1, int l=1, int r=n) {
		if(l > y || r < x) return;
		if(l >= x && r <= y) return tag[now] += k,sum[now] += (r-l+1)*k,void();
		int mid = (l+r)>>1; down(now, l, r);
		go(x, y, k, now<<1, l, mid),go(x, y, k, now<<1|1, mid+1, r);
		up(now);
	}
	ll ask(int x, int y, const int now=1, int l=1, int r=n) {
		if(l > y || r < x) return 0;
		if(l >= x && r <= y) return sum[now];
		int mid = (l+r)>>1; down(now, l, r);
		return ask(x, y, now<<1, l, mid)+ask(x, y, now<<1|1, mid+1, r);
	}
} t1, t2;
signed main() {
	freopen("sh.in", "r", stdin);
	freopen("sh.out", "w", stdout);
	n = read();
	for(int i = 1; i <= n; ++i) a[read()+1] = i;
	mn[1] = mx[1] = a[1];
	for(int i = 2; i <= n; ++i) mn[i] = min(mn[i-1], a[i]),mx[i] = max(mx[i-1], a[i]);
	for(int i = n-1; i; --i) {
		for(int j = mx[i+1]; j > mx[i]; --j) pos1[j] = i;
		for(int j = mn[i+1]; j < mn[i]; ++j) pos2[j] = i;
	}
	for(int i = 1; i <= n; ++i) {
		if(pos1[a[i]]) ans += t1.ask(1, pos1[a[i]]),t2.go(1, pos1[a[i]], 1);
		if(pos2[a[i]]) ans += t2.ask(1, pos2[a[i]]),t1.go(1, pos2[a[i]], 1);
		ans++,_ans += ans;
		t1.go(i, i, 1),t2.go(i, i, 1);
	}
	cout << _ans << "\n";
	return 0;
}