图的遍历(DFS、BFS)

理论：

深度优先搜索（Depth_Fisrst Search）遍历类似于树的先根遍历，是树的先根遍历的推广：

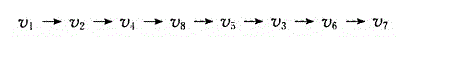
广度优先搜索（Breadth_First Search） 遍历类似于树的按层次遍历的过程：

java实现

Vertex.java

package 图;

public class Vertex{
    String value;
    boolean isVisited;
    Vertex(String value)
    {
        this.value=value;
        this.isVisited=false;
    }
    public String getValue() {
        return value;
    }
    public void setValue(String value) {
        this.value = value;
    }
    public boolean isVisited() {
        return isVisited;
    }
    public void setVisited(boolean isVisited) {
        this.isVisited = isVisited;
    }

}

Edge.java

package 图;

public class Edge{
    Vertex start;
    Vertex end;
    int value;
    public Vertex getStart() {
        return start;
    }

    public void setStart(Vertex start) {
        this.start = start;
    }

    public Vertex getEnd() {
        return end;
    }

    public void setEnd(Vertex end) {
        this.end = end;
    }

    public int getValue() {
        return value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    Edge(Vertex start,Vertex end, int value){
        this.start=start;
        this.end=end;
        this.value=value;
    }
}

Graph.java

package 图;

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.Iterator;
import java.util.List;
import java.util.Stack;

public class Graph {

    public static List<Vertex> vertexList=new ArrayList<Vertex>();
    public static List<Edge> EdgeQueue=new ArrayList<Edge>();public static List<Vertex> depthVertexQueue=new ArrayList<Vertex>();
    public static List<Vertex> breathVertexQueue=new ArrayList<Vertex>();

    public static void buildGraph(){
        Vertex a=new Vertex("a");
        vertexList.add(a);
        Vertex b=new Vertex("b");
        vertexList.add(b);
        Vertex c=new Vertex("c");
        vertexList.add(c);
        Vertex d=new Vertex("d");
        vertexList.add(d);
        Vertex e=new Vertex("e");
        vertexList.add(e);
        Vertex f=new Vertex("f");
        vertexList.add(f);

        addEdge(a,b,0);
        addEdge(a,c,0);
        addEdge(b,d,0);
        addEdge(b,e,0);
        addEdge(c,f,0);

    }

    public static void addEdge(Vertex start,Vertex end,int value){
        Edge e=new Edge(start,end,value);
        EdgeQueue.add(e);
    }

public static Vertex getFirstUnvisitedNeighbor(Vertex origin){

        Vertex unvisitedNeighbor=null;
        Iterator<Edge> iterator=EdgeQueue.iterator();
        while(iterator.hasNext())
        {
            Edge edge=iterator.next();
            if(edge.getStart()==origin)
            {
                if(!edge.getEnd().isVisited)
                {
                    unvisitedNeighbor=edge.getEnd();
                    break;
                }

            }
        }
        return unvisitedNeighbor;
    }

    public static  void depthFirstVisit(Vertex origin){
        if(origin==null)
            return;
        depthVertexQueue.add(origin);
        origin.setVisited(true);

        Vertex curVertex=origin;
        Stack<Vertex> stack=new Stack<Vertex>();
        stack.add(curVertex);

        while(!stack.isEmpty())
        {
            curVertex=stack.peek();
            Vertex tempVertex=getFirstUnvisitedNeighbor(curVertex);
            if(tempVertex!=null)
            {
                depthVertexQueue.add(tempVertex);
                tempVertex.setVisited(true);
                stack.push(tempVertex);
            }
            else
            {
                stack.pop();
            }
        }

    }

    public static void breathFirstVisit(Vertex origin){
        if(origin==null)
            return;

        breathVertexQueue.add(origin);
        origin.setVisited(true);

        List<Vertex> list=new ArrayList<Vertex>();
        Vertex curVertex=origin;
        list.add(curVertex);
        while(!list.isEmpty())
        {
            curVertex=list.remove(0);
            while(getFirstUnvisitedNeighbor(curVertex)!=null)
            {
                Vertex tempVertex=getFirstUnvisitedNeighbor(curVertex);
                breathVertexQueue.add(tempVertex);
                tempVertex.setVisited(true);
                list.add(tempVertex);
            }
        }

    }

    public static void main(String[] args) {
        buildGraph();
        depthFirstVisit(vertexList.get(0));
        for(Vertex each:depthVertexQueue)
            System.out.print(each.getValue()+" ");
    }
}