JavaScript实现队列结构

参考资料

一.什么是队列结构？

1.1.简介

队列(Queue)，类似于栈结构，但又和栈结构不同

• 是一种运算受限的线性表，受限之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作
• 队列结构遵循先进先出(FIFO First In First Out)，图解如下图：
  
  

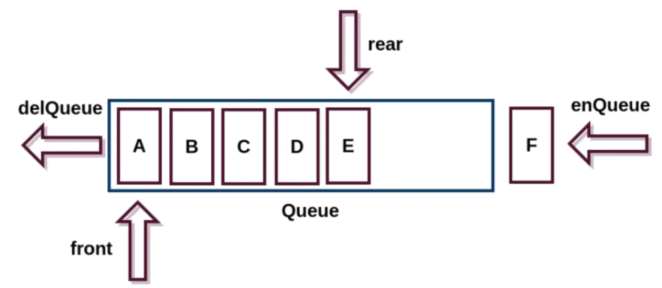
这种结构类似生活中排队的例子：先排先出去

1.2.队列在程序中的应用

• 打印队列：优先放入的文档，优先被取出
• 线程队列：当进行多线程开发时，我们不可能无限制开启新的线程，这个时候使用线程队列，依次按照次序来启动线程并处理任务，减小处理器的压力

二.队列的实现

2.1.队列的封装

队列的操作：

• enqueue(element)：向队列尾部添加一个（或多个）新的项。
• dequeue()：移除队列的第一（即排在队列最前面的）项，并返回被移除的元素。
• front()：返回队列中第一个元素——最先被添加，也将是最先被移除的元素。队列不做任何变动（不移除元素，* 只返回元素信息——与Stack类的peek方法非常类似）。
• isEmpty()：如果队列中不包含任何元素，返回true，否则返回false。
• size()：返回队列包含的元素个数，与数组的length属性类似。
  
  完整封装代码：

      // 封装队列类
      function Queue() {
        // 属性
        this.items = []

        // 方法
        // 1.将元素加入到队列中
        Queue.prototype.enqueue = function (element) {
          this.items.push(element)
        }

        // 2.从队列中删除前端的元素
        Queue.prototype.dequeue = function () {
          return this.items.shift()
        }

        // 3.查看前端的元素
        Queue.prototype.font = function () {
          return this.items[0]
        }

        // 4.查看队列是否为空
        Queue.prototype.isEmpty = function () {
          return this.items.length == 0
        }

        // 5.查看队列中元素的个数
        Queue.prototype.size = function () {
          return this.items.length
        }

        // 6.toString方法
        Queue.prototype.toString = function () {
          var resultString = ''
          this.items.forEach((element) => {
            resultString += element + ' '
          })
          return resultString
        }
      }

测试代码：

      // 使用队列
      var queue = new Queue()

      // 测试操作
      queue.enqueue(1)
      queue.enqueue(2)
      queue.enqueue(3)
      console.log(queue.items) // [1,2,3]
      queue.dequeue()
      queue.dequeue()
      console.log(queue.items) // [3]
      console.log(queue.font()) // 3
      console.log(queue.isEmpty()) // false
      console.log(queue.size()) // 1
      console.log(queue.toString()) // 3

2.2.队列的面试题（击鼓传花）

传入一组数据和设定的数字num，循环遍历数组内元素，遍历到的元素为指定数字num时将该元素删除，直至数组剩下一个元素

代码实现：

      // 面试题：击鼓传花
      function passGame(nameList, num) {
        // 1.创建一个队列结构
        var queue = new Queue()

        // 2.将所有人加入到队列中
        nameList.forEach((item) => {
          queue.enqueue(item)
        })

        // 3.开始数数字
        while (queue.size() > 1) {
          // 不是num的时候，重新加入到队列末尾
          // 是num的时候，将其从队列中删除
          // 3.1.num数字之前的人重新放入到队列的末尾
          for (var i = 0; i < num - 1; i++) {
            queue.enqueue(queue.dequeue())
          }
          // 3.2.num对应的这个人，直接从队列中删除
          queue.dequeue()
          // 思路：每次循环num-1次，当到num次时，队列前端是数据就是需要删除的数据
        }

        // 4.最后剩下的那个人
        console.log(queue.size())
        var endName = queue.font()
        console.log('最终剩下的人是：' + endName)

        return nameList.indexOf(endName)
      }

测试代码：

      // 测试击鼓传花
      // names = ['张三', '李四', '王二', '张麻子']
      // console.log(passGame(names, 3))

三.优先级队列

前面, 我们实现了一种普通的队列. 队列中元素的处理顺序和插入的顺序密切相关.

但是, 还有一种比较常见的场景是和插入顺序无关, 而和元素本身的优先级有关系的队列,这种队列就是优先级队列

优先级队列特点：

• 在插入一个元素的时候会考虑该数据的优先级
• 通过比较优先级, 可以得出这个元素正确的队列中的位置

代码实现：

      function PriorityQueue() {
        // 创建一个内部类 用于保存元素和元素的优先级
        // priority 优先级 在本例子中是越小优先级越大
        function QueueElement(element, priority) {
          this.element = element
          this.priority = priority
        }

        // 封装属性(可以使用链表)
        this.items = []

        // 1.实现插入方法
        PriorityQueue.prototype.enqueue = function (element, priority) {
          // 1.1.创建QueueElement对象
          var queueElement = new QueueElement(element, priority)

          // 1.2.判断队列是否为空
          if (this.items.length === 0) {
            this.items.push(queueElement)
          } else {
            var added = false
            // 1.3.循环比较
            for (let i = 0; i < this.items.length; i++) {
              // 如果大于前一个的优先级
              if (queueElement.priority < this.items[i].priority) {
                // 插入
                this.items.splice(i, 0, queueElement)
                added = true
                break
              }
            }

            // 1.4.如果优先级还是最小，放到最后
            if (!added) {
              this.items.push(queueElement)
            }
          }
        }

        // 2.从队列中删除前端的元素
        PriorityQueue.prototype.dequeue = function () {
          return this.items.shift()
        }

        // 3.查看前端的元素
        PriorityQueue.prototype.font = function () {
          return this.items[0]
        }

        // 4.查看队列是否为空
        PriorityQueue.prototype.isEmpty = function () {
          return this.items.length == 0
        }

        // 5.查看队列中元素的个数
        PriorityQueue.prototype.size = function () {
          return this.items.length
        }

        // 6.toString方法
        PriorityQueue.prototype.toString = function () {
          var resultString = ''
          for (let i = 0; i < this.items.length; i++) {
            resultString +=
              this.items[i].element + '-' + this.items[i].priority + '\n'
          }
          return resultString
        }
      }

测试代码：

      // 测试代码
      var pq = new PriorityQueue()
      pq.enqueue('a', 2)
      pq.enqueue('b', 4)
      pq.enqueue('c', 1)
      pq.enqueue('d', 3)
      // 打印
      console.log(pq.toString())

可以看到，输入的数据被按照优先级从大到下排列

四.总结

以上就是关于队列和其优先级队列的知识点，其实本质还是和栈结构一样都是受限的线性结构，栈是后进先出（LFIO），队列是先进先出（FIFO），一定要将二者结合起来理解！