数据结构之栈(Stack)

什么是栈(Stack)

栈是一种遵循特定操作顺序的线性数据结构，遵循的顺序是先进后出(FILO：First In Last Out)或者后进先出(LIFO：Last In First Out)。

比如：

生活中，厨房里的一摞盘子，你使用的时候会拿最上面的一个，最下面的那个最后使用。这就是FILO。当你想用第二个盘子时，先要拿起第一个，再拿出第二个，然后把第一个放到最上面。

栈的示意图大致如下：

 

 

实现和操作概述

栈的主要操作有以下5种

Object push(Object element) : 向栈顶添加一个元素

Object pop() : 移除栈顶的元素并返回

Object peek() : 返回栈顶元素，但不删除

boolean empty() : 判断栈是否为空，即栈顶是否为空

int search(Object element) :查找element是否存在，存在则返回位置(栈顶为1)，不存在则返回-1。

栈的实现

可以通过数组或链表都可以实现栈，下面都会详细说明。

链表实现是自己写的一个demo。

数组实现以java.util.Stack代码做说明。java中的java.util.Stack类实现是通过数组的。

最后举了一个常见的使用栈实现功能的例子：符号匹配的问题

疑问

对比数组和链表的实现后，个人觉得用链表实现的更好，但JDK种使用的是数组实现。

这个需要进一步了解，或者比较各个操作在运行时间及内存上的变化来分析。//TODO

链表实现在链表首部操作，数组实现在有效数组(数组中有效元素的部分，非数组最大容量)的末尾操作，pop、peek、empty、search操作感觉类似（时间、内存消耗）。

下面做了个简单表格：

链表实现的劣势：需额外信息存储引用，内存浪费；push时需要新建节点。

数组实现的劣势：数组大小不足时，在push时需要扩容。扩容即需要重新分配更大空间并复制数据。

 

	数组	链表
内存浪费	无浪费	有浪费：需存如额外引用信息
动态	非动态：大小无法运行时随意变动	动态的：可以随意增加或缩小
push操作	当数组大小超过时，需要扩容O(n)。 数组大小足够时，直接push完成 O(1)	直接链表首部插入O(1). 但需新建节点

 

 

单链表实现

下面是简易的demo。

通过单链表实现栈很容易实现，push()和pop()直接通过对链表首部的操作即可，时间复杂度都是O(1)。

下面demo很容理解，可以看看注释。需要了解 链表。

public class StackTest<E> {
    public static void main(String[] args) {
        StackTest<Integer> stackTest = new StackTest<>();
        for (int i = 4; i > 0; i--) {
            System.out.println("push:" + stackTest.push(Integer.valueOf(i)).intValue());
        }
        System.out.println("peek:" + stackTest.peek());
        System.out.println("pop:" + stackTest.pop());
        System.out.println("isEmpty:" + stackTest.isEmpty());
        for (int i = 4; i > 0; i--) {
            System.out.println("search " + i + ":" + stackTest.search(Integer.valueOf(i)));
        }
    }    

    //栈顶定义
    StackNode<E> top;

    //节点定义:
    static class StackNode<E> {
        E data;
        StackNode<E> next;

        StackNode(E data, StackNode<E> next) {
            this.data = data;
            this.next = next;
        }
    }

    //向栈顶push一个元素，即向链表首部添加元素
    public E push(E data) {
        top = new StackNode<E>(data, top);
        return top.data;
    }

    //返回栈顶的值。即链表首部节点的值。
    public E peek() {
        if (isEmpty())
            throw new RuntimeException("fail,stack is null!");
        return top.data;
    }

    //从栈顶pop一个元素，即返回栈顶的值 并删除链表第一个节点。
    public E pop() {
        E preTopData = peek();
        top = top.next;
        return preTopData;
    }

    //判空
    public boolean isEmpty() {
        return top == null;
    }

    //查找数据为data的节点位置，栈顶为1.没找到返回-1.
    public int search(E data) {
        int position = 1;
        StackNode<E> currNode = top;

        while (currNode != null && !currNode.data.equals(data)) {
            position++;
            currNode = currNode.next;
        }
        if (currNode == null)
            position=-1;
        return position;
    }
}

push()和pop()操作后，效果为：

打印log为：

push:4
push:3
push:2
push:1
peek:1
pop:1
isEmpty:false
search 4:3
search 3:2
search 2:1
search 1:-1

 

 

栈的数组实现

如上所说，栈的数组实现方式以java.util.Stack类的代码作为说明。

Stack类是继承了Vector类，两个类方法都很多，截取了相关的代码。

主要操作过程：定义一个数组(elementData)存放栈的数据；定义一个变量(elementCount)表示有效元素的个数或范围，也就是栈中的元素；主要操作在有效元素部分的尾部，当push时超过数组大小，数组需要扩容。

大致示意图如下：

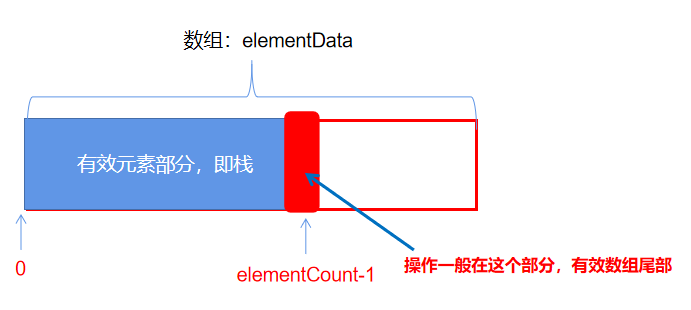
push()操作

Stack<E>类：

public E push(E item) {
    addElement(item);
    return item;
}

Vector<E>类:

默认构造时，数组大小初始化为10。 push()操作即向数组最后一个有效元素位置后填入push的数据。当数组大小不足时，需要扩容。具体看下列注释。

//数组变量定义
protected Object[] elementData;
//有效元素个数，在栈中即表示栈的个数
protected int elementCount;
//当数组溢出时，扩容 增加的大小。
protected int capacityIncrement;
//3种构造方式，默认构造方式的 数组大小初始化为10.
public Vector(int initialCapacity, int capacityIncrement) {
    super();
    if (initialCapacity < 0)
        throw new IllegalArgumentException("Illegal Capacity: "+
                                           initialCapacity);
    this.elementData = new Object[initialCapacity];
    this.capacityIncrement = capacityIncrement;
}

public Vector(int initialCapacity) {
    this(initialCapacity, 0);
}

public Vector() {
    this(10);
}

//增加元素
public synchronized void addElement(E obj) {
    modCount++;
    ensureCapacityHelper(elementCount + 1);
    elementData[elementCount++] = obj;
}

数组扩容

这种扩容方式，如果有相关需求可以作为参考。

private void ensureCapacityHelper(int minCapacity) {
    // overflow-conscious code
    if (minCapacity - elementData.length > 0)
        grow(minCapacity);
}

private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;

private void grow(int minCapacity) {
    // overflow-conscious code
    int oldCapacity = elementData.length;
    int newCapacity = oldCapacity + ((capacityIncrement > 0) ?
                                     capacityIncrement : oldCapacity);
    if (newCapacity - minCapacity < 0)
        newCapacity = minCapacity;
    if (newCapacity - MAX_ARRAY_SIZE > 0)
        newCapacity = hugeCapacity(minCapacity);
    elementData = Arrays.copyOf(elementData, newCapacity);
}

private static int hugeCapacity(int minCapacity) {
    if (minCapacity < 0) // overflow
        throw new OutOfMemoryError();
    return (minCapacity > MAX_ARRAY_SIZE) ?
        Integer.MAX_VALUE :
        MAX_ARRAY_SIZE;
}

 

peek()操作

先看peek()是，由于pop()会调用到。

Stack类：

栈有效个数为elementCount(也是数组有效元素部分)。返回数组第elementCount个元素即可，下标为elementCount-1。

public synchronized E peek() {
    int     len = size();
    if (len == 0)
        throw new EmptyStackException();
    return elementAt(len - 1);
}

Vector类：

public synchronized int size() {
    return elementCount;
}

public synchronized E elementAt(int index) {
    if (index >= elementCount) {
        throw new ArrayIndexOutOfBoundsException(index + " >= " + elementCount);
    }
    return elementData(index);
}

@SuppressWarnings("unchecked")
E elementData(int index) {
    return (E) elementData[index];
}

pop()操作

通过peek获取栈顶元素并作为返回值。再删除栈顶元素。

部分代码上面已有，不列出。

Stack类：

删除数组中有效元素的最后一个，即下标为elementCount-1

public synchronized E pop() {
    E       obj;
    int     len = size();

    obj = peek();
    removeElementAt(len - 1);

    return obj;
}

Vector类:

通用方法，数组中删除某个元素，之后的元素要前移。

实际对于栈，传入的index=elementCount-1。 所以j=0。不需要移动元素，是删除的最后一个元素。

public synchronized void removeElementAt(int index) {
    modCount++;
    if (index >= elementCount) {
        throw new ArrayIndexOutOfBoundsException(index + " >= " +
                                                 elementCount);
    }
    else if (index < 0) {
        throw new ArrayIndexOutOfBoundsException(index);
    }
    int j = elementCount - index - 1;
    if (j > 0) {
        System.arraycopy(elementData, index + 1, elementData, index, j);
    }
    elementCount--;
    elementData[elementCount] = null; /* to let gc do its work */
}

search()操作

查找到后，返回位置。没找到即返回-1。

这个位置相对栈顶，栈顶（1）即数组最后一个有效元素(下标为 size-1)。如果是数组[i]是查找的元素，那么相对栈顶位置即((size-1)- i )+1 = size - i。

Stack类中

public synchronized int search(Object o) {
    int i = lastIndexOf(o);

    if (i >= 0) {
        return size() - i;
    }
    return -1;
}

Vector类中:

public synchronized int lastIndexOf(Object o) {
    return lastIndexOf(o, elementCount-1);
}

public synchronized int lastIndexOf(Object o, int index) {
    if (index >= elementCount)
        throw new IndexOutOfBoundsException(index + " >= "+ elementCount);

    if (o == null) {
        for (int i = index; i >= 0; i--)
            if (elementData[i]==null)
                return i;
    } else {
        for (int i = index; i >= 0; i--)
            if (o.equals(elementData[i]))
                return i;
    }
    return -1;
}

empty()操作

public boolean empty() {
    return size() == 0;
}

栈的使用

符号匹配问题

这里只考虑3对符号，"{}[]()"。匹配规则如代码中，如"{([])}”是符合的，"{([)]}"是不符合的。

思路很简单：符合的情况就是第一个右符合与前面最近的一个左符号是匹配的。

匹配到左符号，压入堆栈；匹配到右符号，与栈顶比较，匹配即符合 pop出栈顶元素；当所有匹配完，栈为空即符合的。

实现代码如下：

public class StackTest<E> {

    public static void main(String[] args) {
        System.out.println(symbolMatch("{for(int i=0;i<10;i++)}"));
        System.out.println(symbolMatch("[5(3*2)+(2+2)]*(2+0)"));
        System.out.println(symbolMatch("([5(3*2)+(2+2))]*(2+0)"));
    }

    public static boolean symbolMatch(String expression) {
        final char CHAR_NULL = ' ';
        if (expression == null || expression.equals(""))
            throw new RuntimeException("expression is nothing or null");

        //StackTest<Character> stack = new StackTest<Character>();
        Stack<Character> stack = new Stack<Character>();
        char[] exps = expression.toCharArray();
        for (int i = 0; i < exps.length; i++) {
            char matchRight = CHAR_NULL;
            switch (exps[i]) {
                case '(':
                case '[':
                case '{':
                    stack.push(Character.valueOf(exps[i]));
                    break;

                case ')':
                    matchRight = '(';
                    break;
                case ']':
                    matchRight = '[';
                    break;
                case '}':
                    matchRight = '{';
                    break;
            }
            if(matchRight == CHAR_NULL)
                continue;
            if (stack.isEmpty())
                return false;
            if (stack.peek().charValue() == matchRight)
                stack.pop();
        }
        if (stack.isEmpty())
            return true;
        return false;
    }
}

输出结果：

true
true
false