tarjan有向图的强连通

强连通：在有向图G中，两个顶点间至少存在一条路径，则两个点强连通。

强连通图：在有向图中，每两个顶点都强连通，则有向图G就是一个强连通图。

强连通分量：在非强连通图中的极大强连通子图，就称为强连通分量。

直接根据定义，可以通过双向遍历取交集的方法求强连通分量，但是其复杂度为O(N^2+M)。更好的方法是用tarjan算法，其时间复杂度为O(N+M)。

tarjan:其实就是对图的深度优先遍历。

算法模拟：

定义 DFN [u]为节点u被搜索到时的次序编号（也就是所遍历的第几个）；

定义LOW[U]为U或者U 的子数能够追溯到最早的栈中节点的次序号。

　　（当DFN[U] ==  LOE[U] 时，以U为根的搜索子树上所有节点是一个强连通分量。实质上就是这个点的整个子树回溯完了，没有链接的路了）

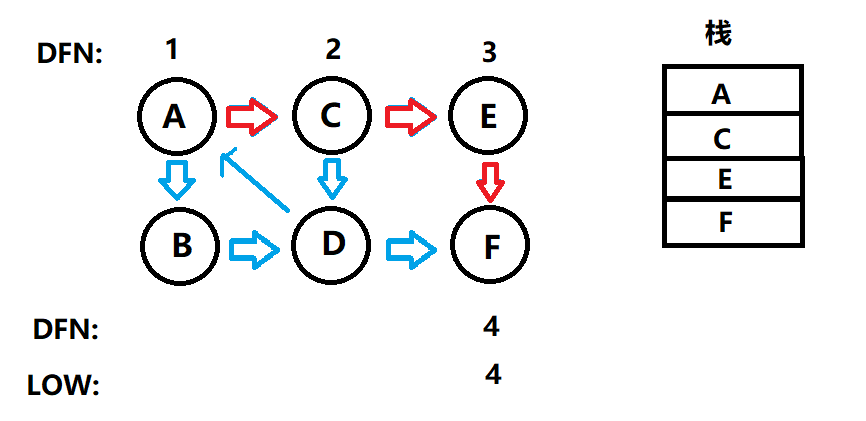
此时的F点DNF[F]==LOW[F]=4，所以F为一个强连通分量，只有它自己本身。

然后返回节点E，此时发现 DFN[E] == LOW[E] =5,所以E也单独为一个强连通分量，只有他本身。

然后返回节点C:

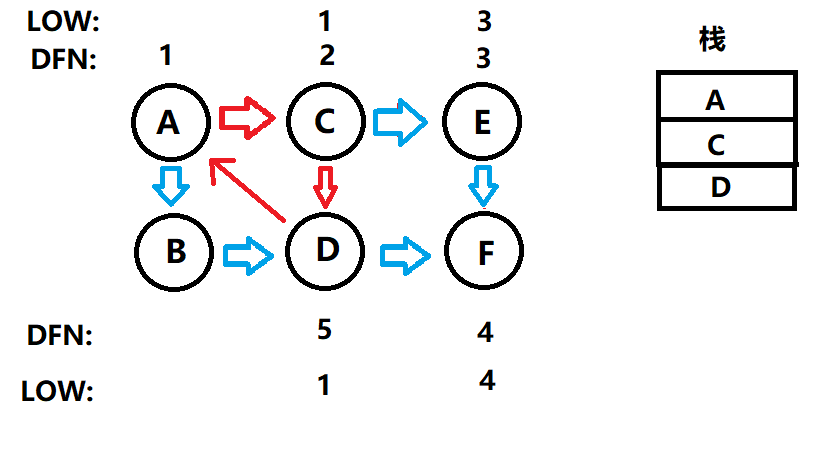
从C节点继续搜其他的C的子树，搜到节点D,将D加入栈中。然后D有  D ->  F ，但是F 已经出栈，所以F节点直接跳过，

还有一个节点A ， 但是呢，A节点已经在栈中，所以LOW[D] = DFN[A] = 1,然后是一个回溯的过程，所以呢，LOW[C] = LOW [D] =1;

所以说明这三个节点已经是一个强连通分量了。

继续回到节点A,最后访问B节点，，然后 B-> D ，然而 D点还在栈中，所以LOW[B] = DFN [ D ] = 5 ,DFN[B] = 6 ;

没有其他点了，算法结束，最后得到 {A,B,C,D} ，{E}, {F}为强连通分量。

在tarjan算法中，每个点只被访问了一次，而且只进行了一次的栈，每条边也只被访问了一次，。所以该算法的时间复杂度为O(N+M);

程序模板：

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 using namespace std;

 #define N 100
 #define M 100

 struct node
 {
     int v;
     int next;
 };

 node edge[M];//边的集合

 int a[N];//顶点的集合
 int instack[N];//模拟栈，标记是否在栈中
 int stack[N];
 int belong[N];//各个顶点属于哪个强连通分量
 int DFN[N];
 int LOW[N];//栈中能够追溯到最早的节点序号
 int n;//点的个数
 int m;//边的个数
 int count;//边的计数器
 int index;//序号（时间戳）
 int top;
 int sun;//强连通分量的个数

 //用邻接表存储
 void add_edge(int u,int v)
 {
     edge[count].next=a[u];
     edge[count].v=v;
     a[u]=count++;
 } 

 void tarjan(int u)
 {
     int i,j;
     int v;
     DFN[u]=LOW[u]=++index;
     instack[u]=true;
     stack[++top]=u;//进栈
     for(i=a[u];i!=-;i=edge[i].next)
     {
         v=edge[i].v;
         if(!DFN[v])//如果DFN[v]为0，没被访问
         {
             tarjan(v);
             //一个回溯的过程
             if(LOW[v]<LOW[u])
                 LOW[u]=LOW[v];
         }
         else
         {
             if(instack[v]&&DFN[v]<LOW[u])
                 LOW[u]=DFN[v];
         }
     }
     if(DFN[u]==LOW[u])
     {
         sun++;
         //出栈
         do
         {
             j=stack[top--];
             instack[j]=false;
             belong[j]=sun;
         }while(j!=u);

     }
 }

 void solve()
 {
     int i;
     top=index=sun=;
     memset(DFN,,sizeof(DFN));
     memset(LOW,,sizeof(LOW));
     for(i=;i<=n;i++)
     {
         if(!DFN[i])
             tarjan(i);
     }
 }

 int main()
 {
     int i,j,k;
     count=;
     memset(a,-,sizeof(a));
     scanf("%d %d",&n,&m);
     for(i=;i<=m;i++)
     {
         scanf("%d %d",&j,&k);
         add_edge(j,k);
     }
     solve();
     for(i=;i<=n;i++)
         printf("%d ",belong[i]);
 }