poj 3710 Christmas Game【博弈论+SG】
也就是转换到树形删边游戏,详见 https://wenku.baidu.com/view/25540742a8956bec0975e3a8.html
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1005;
int T,n,m,cnt,h[N],w[N],s[N],top;
bool v[N],ve[N];
struct qwe
{
int ne,to;
}e[N<<1];
int read()
{
int r=0,f=1;
char p=getchar();
while(p>'9'||p<'0')
{
if(p=='-')
f=-1;
p=getchar();
}
while(p>='0'&&p<='9')
{
r=r*10+p-48;
p=getchar();
}
return r*f;
}
void add(int u,int v)
{
cnt++;
e[cnt].ne=h[u];
e[cnt].to=v;
h[u]=cnt;
}
int dfs(int u)
{
int ans=0;
v[s[++top]=u]=1;
for(int i=h[u];i;i=e[i].ne)
if(!ve[i])
{
int sg;
ve[i]=1,ve[i^1]=1;
if(!v[e[i].to])
sg=dfs(e[i].to)+1;
else
{
while(s[top]!=e[i].to)
w[s[top--]]=1;
return 1;
}
w[e[i].to]?ans^=sg%2:ans^=sg;
}
return ans;
}
int main()
{
while(~scanf("%d",&T))
{
int ans=0;
while(T--)
{
memset(h,0,sizeof(h));
memset(v,0,sizeof(v));
memset(ve,0,sizeof(ve));
memset(w,0,sizeof(w));
top=0;cnt=1;
n=read(),m=read();
for(int i=1;i<=m;i++)
{
int x=read(),y=read();
add(x,y),add(y,x);
}
ans^=dfs(1);
}
ans?puts("Sally"):puts("Harry");
}
return 0;
}
poj 3710 Christmas Game【博弈论+SG】的更多相关文章
- poj 3710 Christmas Game 博弈论
思路:首先用Tarjan算法找出树中的环,环为奇数变为边,为偶数变为点. 之后用博弈论的知识:某点的SG值等于子节点+1后的异或和. 代码如下: #include<iostream> #i ...
- POJ.3710.Christmas Game(博弈论 树上删边游戏 Multi-SG)
题目链接 \(Description\) 给定n棵"树",每棵"树"的节点可能"挂着"一个环,保证没有环相交,且与树只有一个公共点. 两人轮 ...
- POJ3710 Christmas Game 博弈论 sg函数 树的删边游戏
http://poj.org/problem?id=3710 叶子节点的 SG 值为0:中间节点的SG值为它的所有子节点的SG值加1后的异或和. 偶环可以视作一个点,奇环视为一条边(连了两个点). 这 ...
- POJ 3710 Christmas Game#经典图SG博弈
http://poj.org/problem?id=3710 (说实话对于Tarjan算法在搞图论的时候就没搞太懂,以后得找时间深入了解) (以下有关无向图删边游戏的资料来自论文贾志豪<组合游戏 ...
- poj 3710 Christmas Game(树上的删边游戏)
Christmas Game Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 1967 Accepted: 613 Des ...
- POJ 3710 Christmas Game
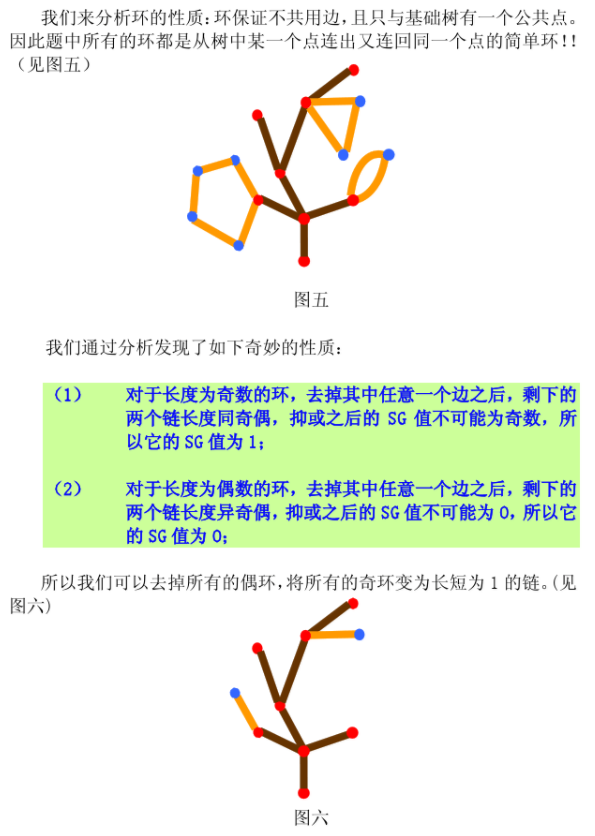
知识储备: 解决办法(奇偶去环): (1) 对于长度为奇数的环,去掉其中任意一个边之后,剩下的 两个链长度同奇偶,抑或之后的 SG 值不可能为奇数,所 以它的 SG 值为 1: (2) 对于长度为 ...
- POJ 3710 Christmas Game [博弈]
题意:略. 思路:这是个删边的博弈游戏. 关于删边游戏的预备知识:http://blog.csdn.net/acm_cxlove/article/details/7854532 学习完预备知识后,这一 ...
- POJ 2960 S-Nim 博弈论 sg函数
http://poj.org/problem?id=2960 sg函数几乎是模板题. 调试代码的最大障碍仍然是手残在循环里打错变量名,是时候换个hydra产的机械臂了[超想要.jpg] #includ ...
- POJ 3710 无向图简单环树上删边
结论题,这题关键在于如何转换环,可以用tarjan求出连通分量后再进行标记,也可以DFS直接找到环后把点的SG值变掉就行了 /** @Date : 2017-10-23 19:47:47 * @Fil ...
随机推荐
- 微信小程序 项目实战(一)生命周期 配置服务器信息 splash启动页
步骤一:小程序 生命周期 //app.js App({ onLaunch: function () { //当小程序初始化完成时,会触发onLaunch(全局只触发一次) }, onShow: fun ...
- sort-list——链表、快慢指针找中间、归并排序
Sort a linked list in O(n log n) time using constant space complexity. 链表,快慢指针找中点,归并排序. 注意判断条件fast-& ...
- 自己定义msi安装包的运行过程
有时候我们须要在程序中运行还有一个程序的安装.这就须要我们去自己定义msi安装包的运行过程. 比方我要做一个安装管理程序,能够依据用户的选择安装不同的子产品.当用户选择了三个产品时,假设分别显示这三个 ...
- SQL常见问题及解决备忘
1.mysql中:you cant't specify tartget table for update in from clause 错误 含义:在同一语句中update或delete某张表的时候, ...
- Mac OS安装Scrapy
个人觉得掌握简单的爬虫知识非常有用,特别是想要从一些特定网站自动地下载一些资源或者统计一些数据,非常的有用.对于产品经理来说,如果要了解竞争产品.替代产品的价格,可以写一个爬虫脚本从各大电商网站爬取相 ...
- 安装sbt
http://www.scala-sbt.org/0.13/docs/zh-cn/Installing-sbt-on-Linux.html [root@hadoop1 target]# curl ht ...
- dedecms5.7二级域名文章图片不显示修改方法.相对路径改为绝对路径的方法
dedecms5.7(织梦CMS5.7)二级域名文章图片不显示修改方法.相对路径改为绝对路径的方法 dedecms升级到5.7SP1后,开启二级域名,你会发现,在二级域名下的文章,上传的图片地址都是: ...
- poj 2771 Guardian of Decency 解题报告
题目链接:http://poj.org/problem?id=2771 题目意思:有一个保守的老师要带他的学生来一次短途旅行,但是他又害怕有些人会变成情侣关系,于是就想出了一个方法: 1.身高差距 ...
- 2014山东省“浪潮杯”第五届ACM省赛总结
一次比赛做一次总结,弱菜又来总结了…… 我这种大四的又死皮赖来混省赛了,貌似就我和山大威海的某哥们(不详其大名)了吧.颁奖前和他聊天,得知他去百度了,真是不错,ORZ之. 比赛流水账: 题目目前不知道 ...
- C#参数数组的用法1
C# 参数数组 有时,当声明一个方法时,您不能确定要传递给函数作为参数的参数数目.C# 参数数组解决了这个问题,参数数组通常用于传递未知数量的参数给函数. params 关键字 在使用数组作为形参时, ...
