Python数据结构应用1——Stack

• Reference: Problem Solving with Algorithms and Data Structures, Release 3.0

自学一下数据结构，学完之后刷leetcode，使用python，从stack开始

Stack建立

class Stack:
    def __init__(self):
        self.items = []

    def is_empty(self):
        return self.items == []

    def push(self,item):
        self.items.append(item)

    def pop(self):
        return self.items.pop()

    def peek(self):
        return self.items[-1]

    def size(self):
        return len(self.items)

以上stack的top位置位于list的ending位置，如果要设置stack的top位置为list的beginning位置，只需要做如下改动

class Stack:
    def __init__(self):
        self.items = []

    def is_empty(self):
        return self.items == []

    def push(self,item):
        self.items.insert(0,item)

    def pop(self):
        return self.items.pop(0)

    def peek(self):
        return self.items[0]

    def size(self):
        return len(self.items)

这两种方式的时间复杂度明显不同，具体可以参见下表中的list处理的时间复杂度

pop(i)和insert(i,item)的时间复杂度为O(n),而pop()和append()的时间复杂度为O(1)

用stack在python中解决实际问题

括号对称问题

这个问题貌似是个很经典的stack问题了，判断string中的括号是否对称：

如：

（）（（）（（（）））） 为对称

（（）（）（（）（（）））） 为不对称

基本思路：

遍历string中的每个字符

1. 当遇到左括号(时，push到stack里
2. 当遇到右括号)时，pop对应的左括号(
3. 如果在遇到右括号)时，此时stack为空，则该右括号)没有对应的左括号，返回False
4. 如果遍历完所有字符后，stack不为空，则stack里全为左括号(，返回False

def par_checker(symbol_string):
    s = Stack()
    balanced = True
    index =0
    while index<len(symbol_string) and balanced:
        symbol = symbol_string[index]
        if symbol == '(':
            s.push(symbol)
        else:
            if s.is_empty():
                balanced = False
            else:
                s.pop()
        index = index+1
    if balanced and s.is_empty():
        return True
    else:
        return False

print(par_checker('()((()))'))
print(par_checker('()(()'))

True
False

运用以上方法，可以解决类似问题，如括号为({[的问题

将十进制数转换为二进制数

很简单，这里用的是高中的方法，除2取余，除2取余……

def divide_by_2(dec_number):
    rem_stack = Stack()
    while dec_number > 0:
        rem = dec_number%2
        rem_stack.push(rem)
        dec_number = dec_number//2
        # '//' 取整除，返回商整数部分
    bin_string = ''
    while not rem_stack.is_empty():
        bin_string = bin_string + str(rem_stack.pop())
    return bin_string
print(divide_by_2(42))

101010

这个方法可以自然的扩展到转换为8进制(octal),16进制(hex)，运用的也是同样的方法，只是在代码的开始建立一个’符号字典’。

def base_converter(dec_number, base):
    digits = '0123456789ABCDEF'
    rem_stack = Stack()
    while dec_number>0:
        rem = dec_number%base
        rem_stack.push(rem)
        dec_number = dec_number//base
    new_string = ''
    while not rem_stack.is_empty():
        new_string = new_string + digits[rem_stack.pop()]
    return new_string

print(base_converter(25, 8))
print(base_converter(30, 16))

31
1E

Infix, Prefix, Postfix相互转换

1、转换的作用：

Something very important has hap- pened. Where did the parentheses go? Why don’t we need them in prefix and postfix? The answer is that the operators are no longer ambiguous with respect to the operands that they work on. Only infix notation requires the additional symbols. The order of operations within prefix and postfix expressions is completely determined by the position of the operator and nothing else. In many ways, this makes infix the least desirable notation to use.

2、转换结果：

简单来说，这一切都跟运算符的先后顺序有关。乘除法的优先率要高于加减法，如果要改变这种定律，只能加括号。而perfix和postfix的表示方法给了一种用加括号的方式来改变这种运算顺序。

Prefix：将运算符置于运算数之前，如
+AB表示A+B；

+A*BC表示A+B*C；

若要表示(?+?)*?，只需写*+ABC(先执行+AB，后执行*(+AB)C)

3、转换方法（postfix）：

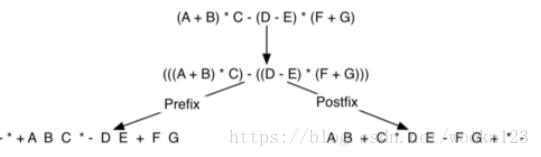
1. 创建一个stack来储存运算符，创建一个list来做输出
2. 将infix表达式转换为list from string
3. 从左往右遍历2中的list,假设每一遍历的元素为token：
   • 如果token是运算数，直接输出
   • 如果token是左括号(，push到stack里
   • 如果token是右括号)，将stack里的元素逐个pop出来并输出直到遇到对应的左括号(
   • 如果token是运算符，push到stack里。然而，在push之前，首先按顺序pop出stack里比该运算符优先级相同或者更高的运算符，并输出。

def infix_to_postfix(infix_expr):
    # 建立一个字典用来表示运算符的优先级：其中左括号的优先级最低
    prec = {}
    prec["*"] =3
    prec["/"] =3
    prec["+"] =2
    prec["-"] =2
    prec["("] =1

    op_stack = Stack()
    postfix_list=[] # output
    token_list = infix_expr.split() 

    for token in token_list:
        # 如果token是运算数，直接输出
        if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
            postfix_list.append(token)
        # 如果token是左括号(，push到stack里
        elif token == '(':
            op_stack.push(token)
        # 如果token是右括号)，将stack里的元素逐个pop出来并输出直到遇到对应的左括号(
        elif token == ')':
            top_token = op_stack.pop()
            while top_token != '(':
                postfix_list.append(top_token)
                top_token = op_stack.pop()
        else:
            # 如果token是运算符，push到stack里。然而，在push之前，首先按顺序pop出stack里比该运算符优先级相同或者更高的运算符，并输出。
            while (not op_stack.is_empty()) and (prec[op_stack.peek()]>=prec[token]):
                postfix_list.append(op_stack.pop())
            op_stack.push(token)

    while not op_stack.is_empty():
        postfix_list.append(op_stack.pop())
    # str.join() 方法用于将序列中的元素以指定的字符连接生成一个新的字符串
    return ' '.join(postfix_list)
print(infix_to_postfix("A * B + C * D"))
print(infix_to_postfix("( A + B ) * C - ( D - E ) * ( F + G )"))

A B * C D * +
A B + C * D E - F G + * -

Postfix使用

当转换成postfix格式后，使用确实是一个问题，但下图已经很好的诠释了这一过程。

1. 创建一个stack用来储存运算数
2. 将string转换成list
3. 从左往右遍历上述list，for evevy token in list：
   • 如果token是一个运算数，将其转换为interger并push到stack中
   • 如果token是一个运算符，它需要两个运算数来进行计算。pop两次，第一次pop的数在左，第二次pop的数在右，并用该运算符进行计算，将计算后的值push到stack里
4. 当list中的值处理完毕，最后的结果在stack中

def postfix_eval(postfix_expr):
    operand_stack = Stack()
    token_list = postfix_expr.split()
    for token in token_list:
        if token in "0123456789":
            operand_stack.push(int(token))
        else:
            operand2 = operand_stack.pop()
            operand1 = operand_stack.pop()
            result = do_math(token, operand1, operand2)
            operand_stack.push(result)
    return operand_stack.pop()
def do_math(op, op1, op2):
    if op == "*":
        return op1 * op2
    elif op == "/":
        return op1 / op2
    elif op == "+":
        return op1 + op2
    else:
        return op1 - op2
print(postfix_eval('7 8 + 3 2 + /'))