machine learning 之 导论 一元线性回归

整理自Andrew Ng 的 machine learnig 课程 week1.

目录：

• 什么是机器学习
• 监督学习
• 非监督学习
• 一元线性回归
  • 模型表示
  • 损失函数
  • 梯度下降算法

1、什么是机器学习

Arthur Samuel不是一个playing checker的高手，但是他编了一个程序，每天和这个程序playing checker，后来这个程序最后变得特别厉害，可以赢很多很厉害的人了。所以Arthur Samuel就给机器学习下了一个比较old，不太正式的定义：

” the field of study that gives the computer the ability to learn without being explicitly programmed “

现代比较正式的一个定义是：

” A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P , if its perfermance at tasks in T as measured by P, improves with experience E  “

也就是说：计算机程序从 ” 做一系列任务T得来的经验E ” 和 “ 测度这个任务做的好不好的表现测度 P “ 中去学习，学习的目标就是，通过这些经验E ，这些任务T做的更好了，做的好不好的评价标准就是P；

以上面Arthur Samuel playing checker的例子来说：

E：Arthur Samuel和程序很多次play checker的经验；

T：playing checker

P：程序在下一次比赛中赢的概率

机器学习问题一般可以分为 ” 监督学习 “ 和 ” 非监督学习 “两类。

2、监督学习

"given data set and already know what our correct output should look like"

对于输入和输出之间的关系我们已经差不多可以有一个思路了

 ” 回归 “ 和 ” 分类 “

回归：结果是连续的，map input to some continuous function （如：预测房价）

分类：结果是离散的，map input to some discrete function （如：预测房价是否大于某个值）

3、非监督学习

” approach problems with little or no ideal what our result should look like “

对于输入和输出之间的关系，我们没有一个概念

” 聚类 “ 和 ” 非聚类 “

聚类：对1000,000中不同的基因聚类，group related to lifespan, height.......

非聚类：鸡尾酒宴会算法，find structure in chaotic environment （比如，在鸡尾酒宴会中各种混杂的声音中识别出某个人的声音或者背景音乐）

4、一元线性回归

模型表示

$x^{(i)}$：输入变量

$y^{(i)}$：输出变量

$(x^{(i)}, y^{(i)})$：一个训练数据

$(x^{(i)}, y^{(i)}); i=1...m$：训练数据集

$X=Y=R$：输入空间和输出空间，这里是一样的

$h_\theta(x)=\theta_0+\theta_1x$

比如以下：

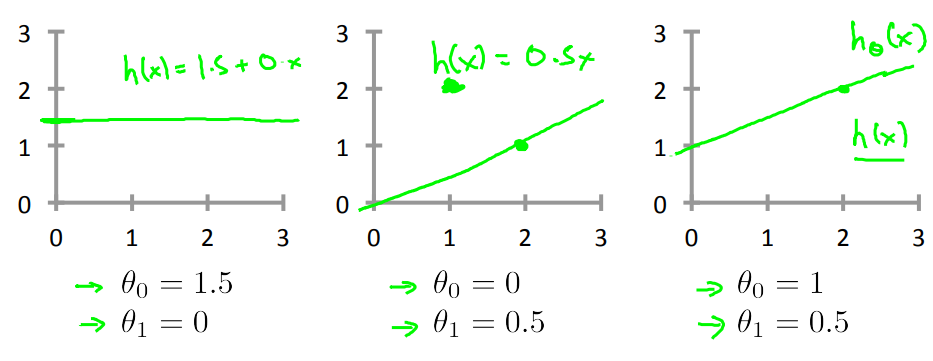
对于监督学习问题：给定训练数据集(x,y)，学习一个$h(x):X\rightarrowY$，对于h(x)是y的一个好的预测

损失函数

用于衡量h(x)的accuracy，是h(x)和y的average difference

$J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i))^2$

这个函数被称为平方损失函数（square error function / mean square error）, 在回归问题中常用于表示损失函数，非回归问题中也会用，比较常用

这里$sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i))^2$ 是损失平方和，$\frac12$是为了以后求导方便加上去的

我们的目标就是找到一个使得损失函数最小的$\theta_0和\theta_1$:

损失函数 visual 1

以下为了展示损失函数，为了方便，让$\theta_0=0$

当$\theta_1=1$时，$J(\theta_1)=0$，在右图绿色叉叉的位置；

当$\theta_1=0.5$时，$J(\theta_1)=~$，大概在右图蓝色叉叉的位置；

当$\theta_1=0$时，$J(\theta_1)=2.～$，大概在右图上y轴的黑色叉叉那里；

基于以上三个点，我们知道$J(\theta_1)$大概就是上右图的样子，当$\theta_1=1$时$J(\theta_1)$最小，左边递减，右边递增；

损失函数 visual 2

对于以上简单的损失函数，我们还可以在二维图上画出来，也比较好理解，但是当维度（变量）大了之后，这种图就不好画了，比如二维：

此时常用等高线图来表示损失函数：

对于以上的训练数据，当$\theta_0=0, \theta_1=360$时，$J(\theta_0, \theta_1)$位于等高线图中红色叉叉的位置；

当$\theta_0, \theta_1$如下左图时，$J(\theta_0, \theta_1)$位于等高线图中绿色叉叉的位置；

当$\theta_0, \theta_1$如下左图时，$J(\theta_0, \theta_1)$位于等高线图中蓝色叉叉的位置，也就是接近最优解的地方，等高线的近似中间位置；

梯度下降算法

那么如何找到最优解呢？梯度下降算法就是一个方法，见以往博客：Gradient Descent