3194. 【HNOI模拟题】化学（无标号无根树计数）

Problem

• 求\(n\)个点的每个点度数不超过\(4\)的无标号无根树个数.

Data constraint

• \(1\le n\le 500\)

Solution

• 尝试着把问题一般化。我们来考虑一个这样的问题：求\(n\)个节点，每个节点度数不超过\(m\)的无根树个数。

• 为了解决这个问题，我们不妨先来解决有根树的情况。注意这里的树都是无标号的。所以每一种合法树的根的子树的\(size\)都可以看做是单调的。然而无根树的计数比较繁琐。例如在无根树中以下两种情况视作同一种：
  
  

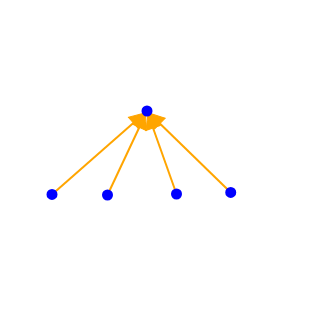
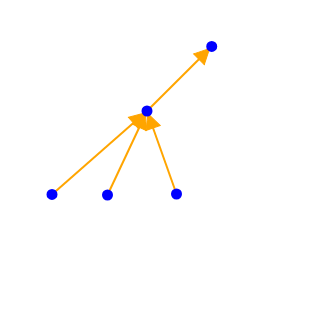
• 而在有根树情况下，这两种方案显然是不一样的。但注意，对于有根树这两种情况也是一样的：

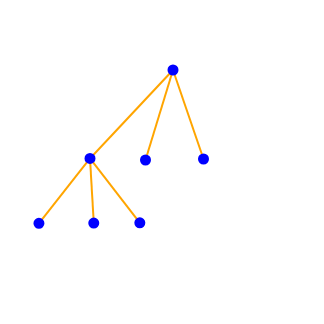
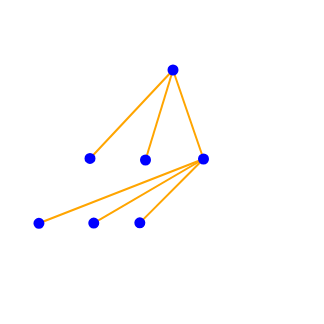
• 所以转化成有根树，我们可以更方便的进行DP。并且通过上面这两幅图我们发现唯一需要注意的是子树\(size\)间的关系。

• 不妨令\(f_{i,j}\)表示当前根节点度为\(j\)，总共有\(i\)个节点时的方案数。此外，我们理应记录一下当前子树的最大\(size\)，然后每次枚举个更大的\(size\)去尝试着转移。但实质上我们可以不用记录，因为我们可以直接从小到大枚举这个\(size\)，然后转移.

• 枚举当前最大子树的个数\(k\)，令\(s=\sum^{m−1}_{k=0}f(size,k)\)，我们不难写出这样一个式子：

\[f(i,j)=\sum_{k}f(i−size×k,j−k)\left\{ \begin{matrix}s+k-1\\k \end{matrix} \right\}
\]

• 其中\(\left\{ \begin{matrix}s+k-1\\k \end{matrix} \right\}\)表示的是在\(s\)个盒子中放\(k\)个球，盒子不同，球相同，可以重复放的方案。这正好符合我们的要求。不难发现，我们这样枚举的\(size\)一定可以保证子树是单调的，那么避免了算重。

• 解决了有根树，我们现在来考虑无根树的问题。事实上，有一个极其巧妙且重要的性质：两颗无根树同构，则以它们重心为根的有根树同构

• 那么我们就只需保证\(size\le (n-1)>>1\)即可。

• 唯一需要注意的是，当一棵树有两个重心的时候，我们的\(size\)都是小于\(\frac{n}{2}\)的，所以我们要特殊处理一下两个\(size=\frac{n}{2}\)的拼接，这也同样是一个组合数。与上面的处理是一样的

• 最后是丧病的高精度：

Code

#include <bits/stdc++.h>

#define F(i, a, b) for (int i = a; i <= b; i ++)
#define G(i, a, b) for (int i = a; i >= b; i --)
#define mem(a, b) memset(a, b, sizeof a)

const int N = 501, M = 4, T = 250;

using namespace std;

int n;

struct Data {
	int len, a[T];
	Data() { len = 0, mem(a, 0); }

	friend Data operator + (Data a, Data b) {
		Data c; c.len = max(a.len, b.len);
		F(i, 1, c.len)
			c.a[i] += a.a[i] + b.a[i], c.a[i + 1] += c.a[i] / 10000, c.a[i] %= 10000;
		c.len += (c.a[c.len + 1] > 0);

		return c;
	}

	friend Data operator < (Data a, int b) {
		a.a[1] += b;
		for (int i = 1; i <= a.len; i ++)
			a.a[i + 1] += a.a[i] / 10000, a.a[i] %= 10000, a.len += (a.a[a.len + 1] > 0);
		return a;
	}
	friend Data operator > (Data a, int b) {
		a.a[1] -= b;
		for (int i = 1; i <= a.len; i ++)
			if (a.a[i] < 0) a.a[i] += 10000, a.a[i + 1] --;
		while (a.a[a.len] == 0) a.len --;
		return a;
	}

	friend Data operator * (Data a, int b) {
		Data c; c.len = a.len;
		F(i, 1, c.len)
			c.a[i] = a.a[i] * b;
		for (int i = 1; i <= c.len; i ++)
			c.a[i + 1] += c.a[i] / 10000, c.a[i] %= 10000, c.len += (c.a[c.len + 1] > 0);

		return c;
	}

	friend Data operator & (Data a, Data b) {
		Data c; c.len = a.len + b.len;
		F(i, 1, a.len)
			F(j, 1, b.len) {
				c.a[i + j - 1] += a.a[i] * b.a[j];
				c.a[i + j] += c.a[i + j - 1] / 10000;
				c.a[i + j - 1] %= 10000;
			}
		while (c.a[c.len] == 0) c.len --;

		return c;
	}

	friend Data operator / (Data a, int b) {
		Data c; int x = 0;
		G(i, a.len, 1) {
			x = x * 10000 + a.a[i];
			if (x >= b)
				c.a[++ c.len] = x / b, x %= b;
			else
				if (c.len) c.len ++;
		}
		F(i, 1, c.len >> 1) swap(c.a[i], c.a[c.len - i + 1]);

		return c;
	}

} f[N][M + 1], Ans;

Data C(Data x, int y) {
	Data ans; ans.a[1] = ans.len = 1; int mul = 1;
	F(i, 1, y) {
		Data X;
		X = x > (i - 1);
		ans = ans & X;
		mul = mul * i;
	}
	return ans / mul;
}

int main() {
	scanf("%d", &n), f[1][0].a[1] = f[1][0].len = 1;

	F(mx, 1, n - 1 >> 1) {
		Data s;
		F(i, 0, M - 1)
			s = s + f[mx][i];
		G(i, n, mx + 1)
			F(j, 1, M)
				F(k, 1, min(j, i / mx)) {
					Data t = s < (k - 1);
					Data R = C(t, k);
					Data T = f[i - k * mx][j - k] & R;
					f[i][j] = f[i][j] + T;
				}
	}

	F(i, 0, M)
		Ans = Ans + f[n][i];
	if (!(n & 1)) {
		Data s;
		F(i, 0, M - 1)
			s = s + f[n >> 1][i];
		s = s < 1;
		Ans = Ans + C(s, 2);
	}

	printf("%d", Ans.a[Ans.len]);
	G(i, Ans.len - 1, 1)
		printf("%04d", Ans.a[i]);
}