问题描述：

求点(x1, y1)关于点(x0, y0)逆时针旋转a度后的坐标

思路：

1、首先可以将问题简化，先算点(x1, y1)关于源点逆时针旋转a度后的坐标，求出之后加上x0，y0即可。

2、关于源点旋转，用极坐标表示

设x1 = Rcos(θ), y1 = Rsin(θ)，绕源点逆时针旋转β度后得到坐标(x2, y2)等于(Rcos(θ + β) , Rsin(θ + β))

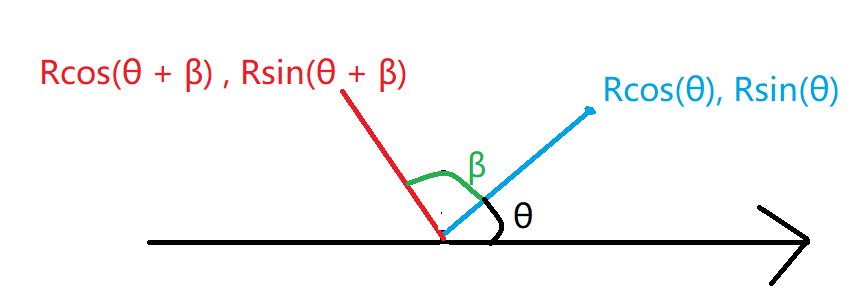
3、展开(Rcos(θ + β) , Rsin(θ + β))

变成 x2 = Rcos(θ)cos(β) - Rsin(θ)sin(β) 　　y2 = Rsin(θ)cos(β) + Rcos(θ)sin(β)

结合上面的x1 = Rcos(θ), y1 = Rsin(θ)

得到：x2 = x1cos(β) - y1sin(β)   　　y2 = x1sin(β) + y1cos(β)

4、转化成一般形式

x2 = (x1 - x0)cos(β) - (y1 - y0)sin(β) + x0   　　

y2 = (x1 - x0)sin(β) + (y1 - y0)cos(β) + y0

点(x1, y1)关于点(x0, y0)逆时针旋转a度后的坐标求解的更多相关文章

  1. 将一个4X4的数组进行逆时针旋转90度后输出，要求原数组数据随机输入

    //将一个4X4的数组进行逆时针旋转90度后输出,要求原数组数据随机输入 #include<stdio.h> int main() { int a[4][4],b[4][4],i,j;// ...

  2. PyOpenCV图像逆时针旋转90度

    warpAffine方法效果很搓,留下大片黑色区域. 使用flip和transpose可以实现逆时针旋转90度.先flip或先transpose均可. #coding:utf-8 import cv2 ...

  3. 点（x3,y3）到经过点（x1,y1）和点（x2,y2）的直线的最短距离

    /// <summary> /// 点(x3,y3)到经过点(x1,y1)和点(x2,y2)的直线的最短距离 /// </summary> /// <param name ...

  4. [javascript svg fill stroke stroke-width x1 y1 x2 y2 line stroke-opacity fill-opacity 属性讲解] svg fill stroke stroke-width stroke-opacity fill-opacity line绘制线条属性讲解

    <!DOCTYPE html> <html lang='zh-cn'> <head> <title>Insert you title</title ...

  5. 买茶叶想到的哪个比较便宜 x1/y1 >x2/y2 x代表多少钱 y代表 多少克 无聊的试炼

    茶叶1 128元     200克 茶叶2  330元    160克 当然这个哪个便宜 一眼就知道了,这里不过抛砖引玉 128元    330元 200克    160克 我们把价钱用x表示 多少克 ...

  6. hdu5794 A Simple Chess 容斥+Lucas 从(1,1)开始出发，每一步从(x1,y1)到达(x2,y2)满足(x2−x1)^2+(y2−y1)^2=5, x2>x1,y2>y1; 其实就是走日字。而且是往(n,m)方向走的日字。还有r个障碍物，障碍物不可以到达。求(1,1)到(n,m)的路径条数。

    A Simple Chess Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)To ...

  7. 现在有一张半径为r的圆桌，其中心位于(x,y)，现在他想把圆桌的中心移到(x1,y1)。每次移动一步，都必须在圆桌边缘固定一个点然后将圆桌绕这个点旋转。问最少需要移动几步。

    // ConsoleApplication5.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" #include<vector> ...

  8. openCv 图像顺时针、逆时针旋转

    通过下面这个函数调用 Rotate90(workImg,270); //顺时针旋转 Rotate90(workImg,90); //逆时针旋转 实现,其实用该函数旋转任意度数对正方形图都ok,只是长方 ...

  9. 已知直线上的两点 A(x1, y1), B(x2, y2) 和另外一点 C(x0, y0)，求C点到直线的距离。

    数学知识太差,一点点积累,高手勿喷. 1. 先求出AB向量 a = ( x2-x1, y2-y1 ) 2. 求AB向量的单位方向向量 b = √((x2-x1)^2 + (y2-y1)^2)) a1 ...

随机推荐

  1. 第四章 使用jQuery操作DOM

    第四章 使用jQuery操作DOM 一.DOM操作 在jQuery中的DOM操作主要可分为样式操作.文本和value属性值操作.节点操作: 节点操作又包含属性操作.节点遍历和CSS-DOM操作. 其中 ...

  2. Hey，man，are you ok? －－ 关于心跳、故障监测、lease机制

    电话之于短信.微信的一个很大的不同点在于,前者更加及时,有更快速直接的反馈:而后面两个虽然称之为instant message,但经常时发出去了就得等对方回复,等多久是不确定的.打电话能明确知道对方在 ...

  3. vue表单详解——小白速会

    一.基本用法 你可以用 v-model 指令在表单 <input> 及 <textarea> 元素上创建双向数据绑定. 但 v-model 本质上不过是语法糖.它负责监听用户的 ...

  4. Python内置函数(4)——min

    英文文档: min(iterable, *[, key, default]) min(arg1, arg2, *args[, key]) Return the smallest item in an ...

  5. python 面向对象之多态与绑定方法

    多态与多态性 一,多态 1,多态指的是一类事物有多种形态(python里面原生多态) 1.1动物有多种形态:人,狗,猪 import abc class Animal(metaclass=abc.AB ...

  6. Spring Cloud的DataRest（二）

    一.创建工程 1.主程序 2.依赖 3.配置 二.案例开发 1.entity 2.repository 三.案例验证 安装postman4.13,启动应用,执行如下案例验证! 1.create - p ...

  7. docker实践3

    我的docker学习笔记3   $docker run ubuntu echo'hello world' $docker run -i -t ubuntu /bin/bash #ps -ef #exi ...

  8. Web框架之Django基础篇

    Web框架之Django基础篇   本节介绍Django 简介,安装 基本配置及学习  路由(Urls).视图(Views).模板(Template).Model(ORM). 简介 Django 是一 ...

  9. Android学习——NDK交叉编译

    原创作品,转载请注明出处,严禁非法转载.如有错误,请留言! email:40879506@qq.com 一. 环境1.GNU/Linux Ubuntu12.04操作系统(x86) 二. 下载NDK安装 ...

  10. Scrapy抓取Quotes to Scrape

    # 爬虫主程序quotes.py # -*- coding: utf-8 -*- import scrapy from quotetutorial.items import QuoteItem # 启 ...