超强视频超分AI算法，从此只看高清视频

最近发现一个特别强的视频超分算法————BasicVSR，在真实世界数据集中，实现了前所未有的视觉重建效果，最近它还拿下了超分比赛NTIRE 2021三冠一亚的优异成绩，登上了CVPR 2022。

视频超分，假设低分辨率视频是从高分辨率的视频经过一系列的退化操作而得到，超分算法就是将该退化操作进行求逆，从而可以将低分辨率视频恢复成高分辨率视频。

对算法细节感兴趣的同学可以先研究一下论文『Investigating Tradeoffs in Real-World Video Super-Resolution』

我试玩了一下，感觉效果还是蛮不错的，下面就分享一下BasicVSR在ubuntu下的安装极简教程。

实不相瞒，macOS和ubuntu下我都安装成功了，Windows没有成功（老报错），感兴趣且运气爆表的同学可以再试试。

安装

1 创建环境

conda create -n realbasic python=3.8

2 安装pytorch

https://pytorch.org/get-started/locally/

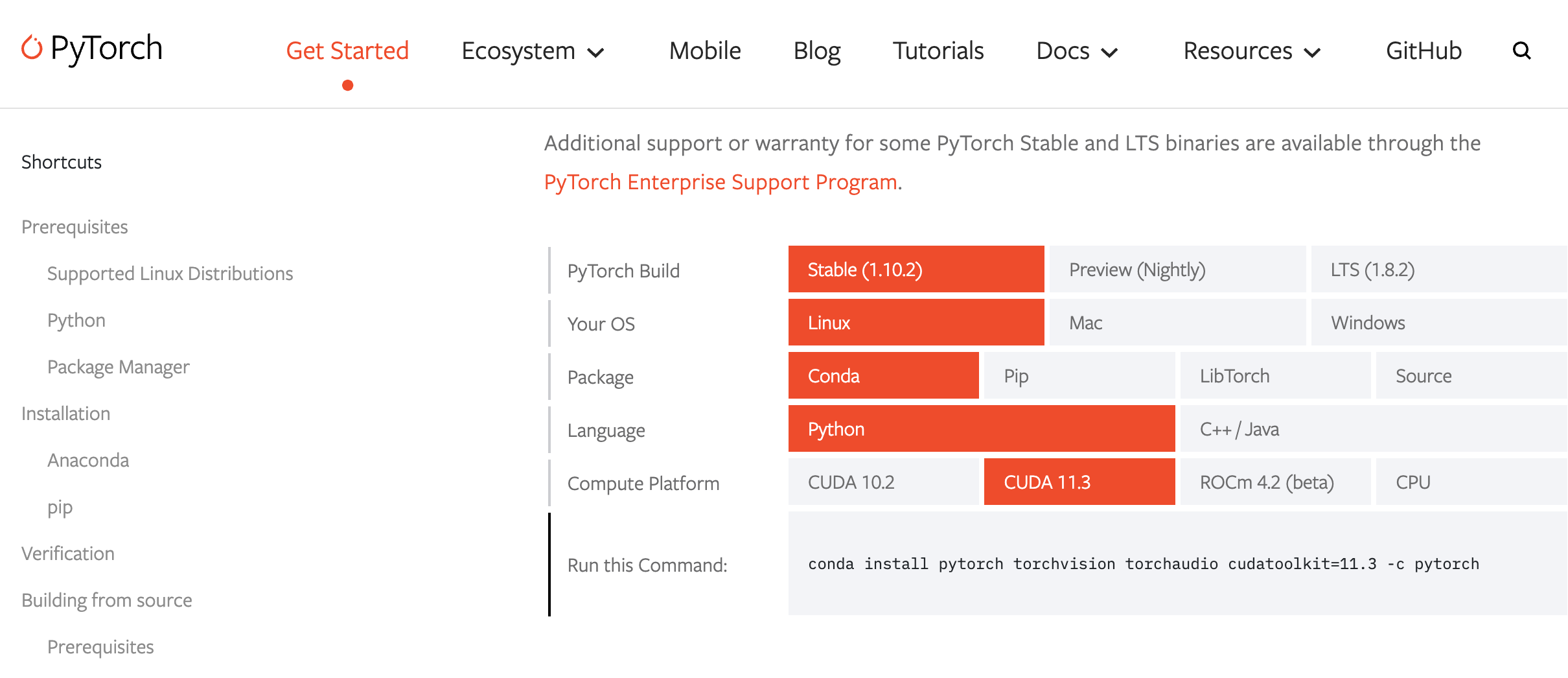
具体版本需根据自己的电脑配置，如有GPU，需与注意自己的cuda版本，可以使用nvidia-smi查看。

conda install pytorch==1.7.1 torchvision==0.8.2 torchaudio==0.7.2 cudatoolkit=10.1 -c pytorch

3 安装mim 和 mmcv-full

MMCV 是一个面向计算机视觉的基础库，它支持了很多开源项目。建议安装完整版:mmcv-full ，包含所有的特性以及丰富的开箱即用的 CUDA 算子。

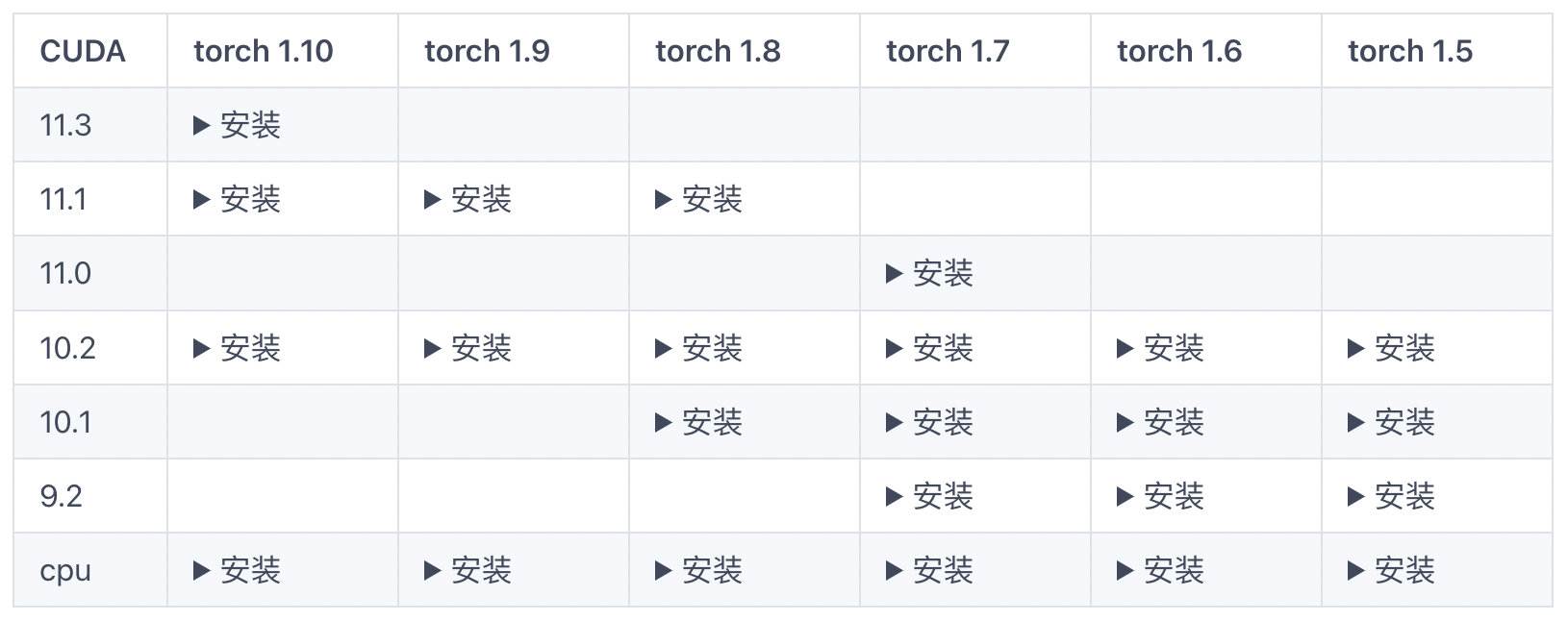
但是直接pip安装需注意cuda和torch版本，容易安装失败。建议使用MIM安装，它会自动检查 CUDA 和 PyTorch 环境并尽量帮我们安装和环境匹配的预编译版本的 MMCV-full，从而省去编译的耗时。

pip install openmim
mim install mmcv-full

4 安装MMEditing

MMEditing 是基于 PyTorch 的图像&视频编辑开源工具箱, 提供修复/抠图/超分辨率/生成等任务最先进的算法。用pip我试了也失败了几次，最后只能本地安装：

git clone https://github.com/open-mmlab/mmediting.git
cd mmediting
pip install -r requirements.txt
# 如报错，忽略即可，继续执行下指令
pip install -v -e .

使用

1 克隆项目

https://github.com/ckkelvinchan/RealBasicVSR

2 下载预训练模型

下载地址：

在RealBasicVSR项目下新建checkpoints文件夹

3 运行

将需要转换的视频放到data目录下，运行即可

python inference_realbasicvsr.py configs/realbasicvsr_x4.py checkpoints/RealBasicVSR_x4.pth data/demo_001.mp4 results/demo_001.mp4 --fps=12.5

4 结果

运行比较耗时，需耐心等待，如果你有钞能力，当我没说。