KMP 算法实现

# coding=utf-8
def get_next_list(findding_str):  # O(m)
    # 求一个字符串序列每个位置的最长相等前、后缀
    j = 0  # 最长相等前缀的末位
    next = [0]  # next 数组用于保存字符串每个位置的最长相等前、后缀的长度值
    # i 是最长相等后缀的末位
    for i in range(1, len(findding_str)):
        while j > 0 and findding_str[i] != findding_str[j]:
            # 如果当前 前缀末位（j）字符与当前i位置的字符不相等时，j回退 PS：j的值也表示findding_str[：i+1]最长相等前、后缀的长度值
            j = next[j-1]
        if findding_str[i] == findding_str[j]:
            j += 1
        next.append(j)
    return next
def KMP(findding_str, next, parent_str):  # O(n)
    ind = 0
    for i in range(len(parent_str)):
        while parent_str[i] != findding_str[ind]:
            if ind == 0:
                break
            # parent_str[i] != findding_str[ind]  且  ind != 0 时，从findding_str[ind] 左侧的字符串的最大相等前缀处开始比较
            ind = next[ind-1]
        if parent_str[i] == findding_str[ind]:
            ind += 1
            if ind == len(findding_str):
                print(i, ind, parent_str[i - ind + 1: i+1])
                ind = 0
                # break
if __name__ == '__main__':
    parent_str = 'aabafgggahaabaafaabaahatjhrtjabaafaabaahaabaafaabaahaabaaf'
    findding_str = 'aabaaf'
    KMP(findding_str, get_next_list(findding_str), parent_str)

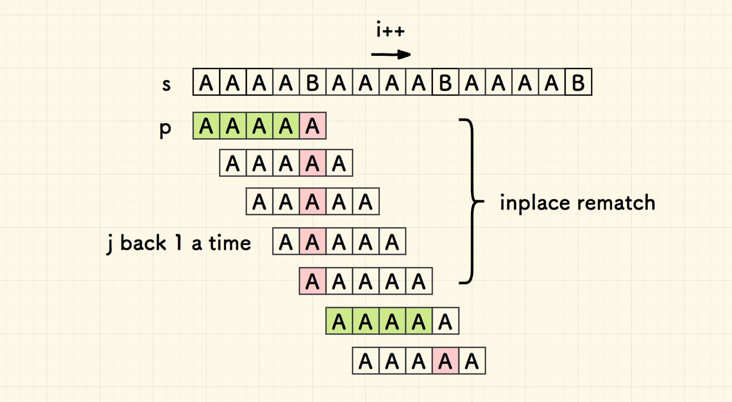
当在 j 处失配时，j -> next[j] 是说回溯到位置 next[j]

注意，next[j] 的位置的含义是什么？是对齐了已经匹配好的串的位置。

下图中，红色的方格是失配处。一旦失配，j 发生回溯跳转，

因为新位置左边的串已经是匹配好的（这正是 next 数组的含义，前后公共缀的长度），所以无需回溯到头。



按上面的图，数一数，绿色的是匹配上的字符，红色的是失配的地方，横向 n 个，

纵向 m 个，总共 m + n 次比对。

每次失配，子串回溯，对齐已匹配串，在失配处原地再匹配一次主串对应字符

所以，kmp 的比对次数是 (n + 失配次数）

KMP 算法的最差情况的一个案例，n/m 个失配点位，每个点位重新匹配 m-1 次，此时总共比对 n+(m-1)*(n/m) 次，接近 2n 次。

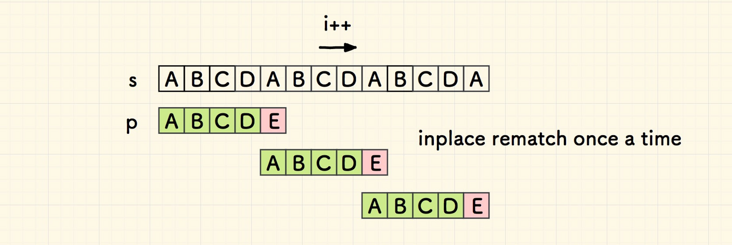
如果不考虑搜索到的情况，最好情况如下，总共比对 n+1*(n/m) 次，如果 m 很小，也接近 2n 次，如果 m 比较大，就接近 n 次。

算上预处理阶段O(m)，KMP 在最好、最坏的情况下的时间复杂度都是 O(m+n)

参考链接：https://segmentfault.com/q/1010000014560162