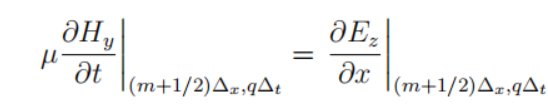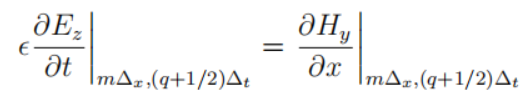[读书笔记]FDTD与YEE晶胞
截图选自Understanding the Finite-Difference Time-Domain Metho 作者是John B. Schneider
有限差分时域(FDTD)方法使用有限差分作为麦克斯韦方程组(特别是安培定律和法拉第定律)的近似。
麦克斯韦方程组乃是由四个方程共同组成的:
- 高斯定律:该定律描述电场与空间中电荷分布的关系。电场线开始于正电荷,终止于负电荷(或无穷远)。计算穿过某给定闭曲面的电场线数量,即其电通量,可以得知包含在这闭曲面内的总电荷。更详细地说,这定律描述穿过任意闭曲面的电通量与这闭曲面内的电荷之间的关系。
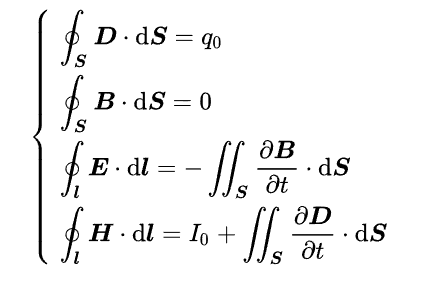
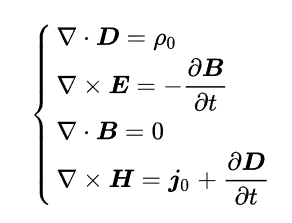
考虑函数f (x)围绕点x0展开的Taylor级数展开式,其偏移量为±δ/2:
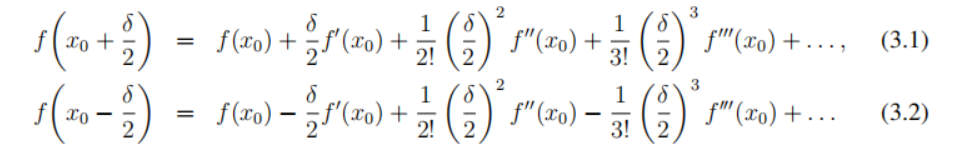
两式相减可得
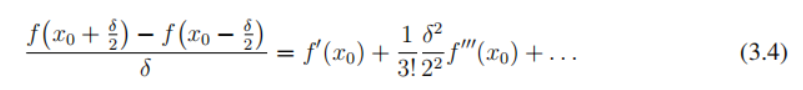
整理一下可以变成
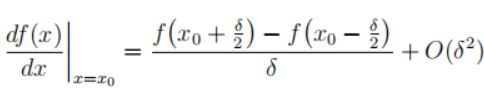
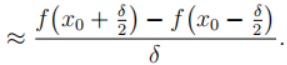 左边为关于位移的导数右边为中心差分与高阶无穷小,近似等于中心差分(在极限下,当δ趋于零时,近似就变得精确)
左边为关于位移的导数右边为中心差分与高阶无穷小,近似等于中心差分(在极限下,当δ趋于零时,近似就变得精确)
由Kane Yee在1966年首次提出的FDTD算法采用了二阶中心差异。该算法可总结如下:


1.用有限差分代替安培定律和法拉第定律中的所有导数
2.求解得到的差分方程,得到“更新方程”,用(已知的)过去的场来表示(未知的)未来的场。
3.在未来的一个时间步中评估磁场与
4.在未来的一个时间步中评估磁场与
5.重复循环
在一维FDTD中法拉第定律可以写作:
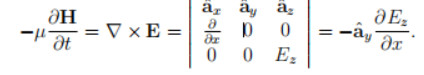 变为标量形式为:
变为标量形式为: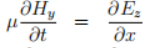 根据电场的空间导数给出了磁场的时间导数。
根据电场的空间导数给出了磁场的时间导数。
安培定律可以写作:
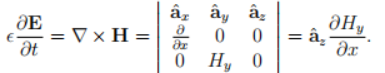 变为标量形式为:
变为标量形式为: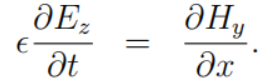 根据磁场的空间导数给出了电场的时间导数。
根据磁场的空间导数给出了电场的时间导数。
再用有限的差值替换上式中的导数以做到离散化
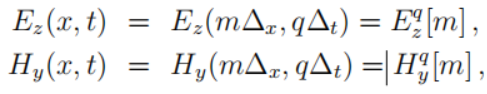 m表示空间步,q表示时间步
m表示空间步,q表示时间步
如下图所示,第一个方程将用于及时推进磁场,而第二个方程将用于推进电场。一种方法,其中一个场是先进的,然后是另一个场,然后重复这个过程,被称为跳蛙法。
 更新磁场后
更新磁场后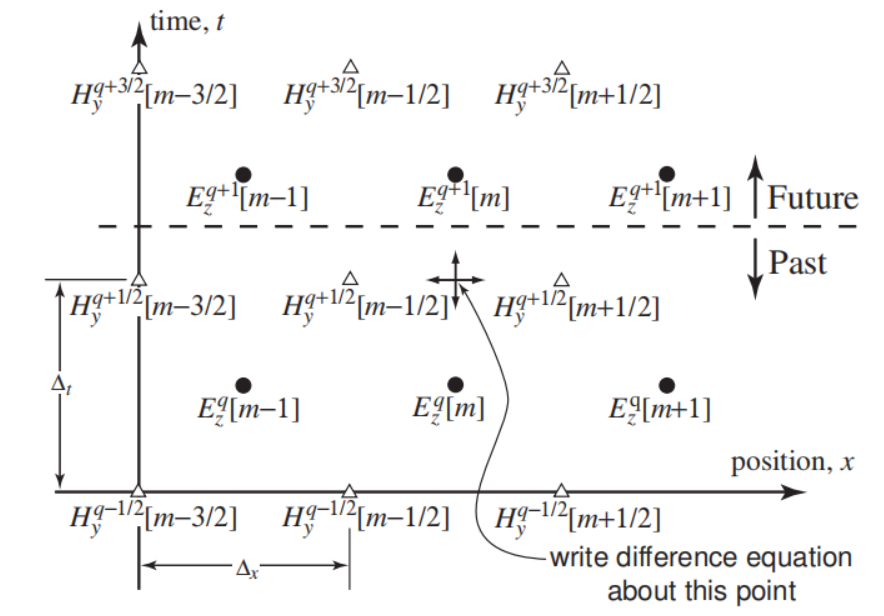
上图更新主要涉及两个差分等式:
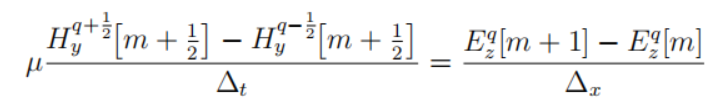 整理可得
整理可得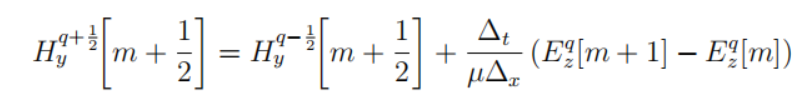 代表过去半个时刻的两个相邻位置电场以及过去一个时刻的磁场推导出未来半个时刻的磁场
代表过去半个时刻的两个相邻位置电场以及过去一个时刻的磁场推导出未来半个时刻的磁场
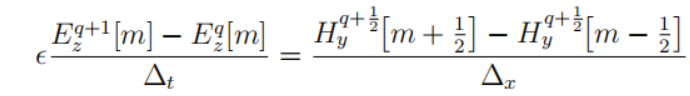 整理可得
整理可得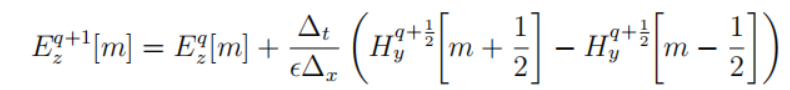 代表过去半个时刻的两个相邻位置磁场以及过去一个时刻的电场推导出未来半个时刻的电场
代表过去半个时刻的两个相邻位置磁场以及过去一个时刻的电场推导出未来半个时刻的电场
转换成代码就是两句赋值语句(imp0代表自由空间的特征阻抗):
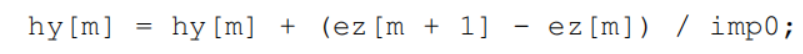
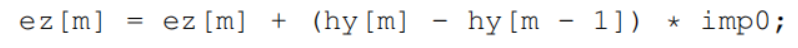
下面为简要代码:
1 /* Bare-bones 1D FDTD simulation with a hard source. */
2
3 #include <stdio.h>
4 #include <math.h>
5
6 #define SIZE 200
7
8 int main()
9 {
10 double ez[SIZE] = {0.}, hy[SIZE] = {0.}, imp0 = 377.0;
11 int qTime, maxTime = 250, mm;
12
13 /* do time stepping */
14 for (qTime = 0; qTime < maxTime; qTime++) {
15
16 /* update magnetic field */
17 for (mm = 0; mm < SIZE - 1; mm++)
18 hy[mm] = hy[mm] + (ez[mm + 1] - ez[mm]) / imp0;
19
20 /* update electric field */
21 for (mm = 1; mm < SIZE; mm++)
22 ez[mm] = ez[mm] + (hy[mm] - hy[mm - 1]) * imp0;
23
24 /* hardwire a source node */
25 ez[0] = exp(-(qTime - 30.) * (qTime - 30.) / 100.);
26
27 printf("%g\n", ez[50]);
28 } /* end of time-stepping */
29
30 return 0;
31 }
[读书笔记]FDTD与YEE晶胞的更多相关文章
- 读书笔记汇总 - SQL必知必会(第4版)
本系列记录并分享学习SQL的过程,主要内容为SQL的基础概念及练习过程. 书目信息 中文名:<SQL必知必会(第4版)> 英文名:<Sams Teach Yourself SQL i ...
- 读书笔记--SQL必知必会18--视图
读书笔记--SQL必知必会18--视图 18.1 视图 视图是虚拟的表,只包含使用时动态检索数据的查询. 也就是说作为视图,它不包含任何列和数据,包含的是一个查询. 18.1.1 为什么使用视图 重用 ...
- 《C#本质论》读书笔记(18)多线程处理
.NET Framework 4.0 看(本质论第3版) .NET Framework 4.5 看(本质论第4版) .NET 4.0为多线程引入了两组新API:TPL(Task Parallel Li ...
- C#温故知新:《C#图解教程》读书笔记系列
一.此书到底何方神圣? 本书是广受赞誉C#图解教程的最新版本.作者在本书中创造了一种全新的可视化叙述方式,以图文并茂的形式.朴实简洁的文字,并辅之以大量表格和代码示例,全面.直观地阐述了C#语言的各种 ...
- C#刨根究底:《你必须知道的.NET》读书笔记系列
一.此书到底何方神圣? <你必须知道的.NET>来自于微软MVP—王涛(网名:AnyTao,博客园大牛之一,其博客地址为:http://anytao.cnblogs.com/)的最新技术心 ...
- Web高级征程:《大型网站技术架构》读书笔记系列
一.此书到底何方神圣? <大型网站技术架构:核心原理与案例分析>通过梳理大型网站技术发展历程,剖析大型网站技术架构模式,深入讲述大型互联网架构设计的核心原理,并通过一组典型网站技术架构设计 ...
- LOMA280保险原理读书笔记
LOMA是国际金融保险管理学院(Life Office Management Association)的英文简称.国际金融保险管理学院是一个保险和金融服务机构的国际组织,它的创建目的是为了促进信息交流 ...
- 《3D Math Primer for Graphics and Game Development》读书笔记2
<3D Math Primer for Graphics and Game Development>读书笔记2 上一篇得到了"矩阵等价于变换后的基向量"这一结论. 本篇 ...
- 《3D Math Primer for Graphics and Game Development》读书笔记1
<3D Math Primer for Graphics and Game Development>读书笔记1 本文是<3D Math Primer for Graphics and ...
- 《More Effective C#》读书笔记
<More Effective C#>这本书,大概是四年前看完的,但只整理了一部分读书笔记,后面有时间的话,会陆续补充的. More Effective C# :使用泛型 More Eff ...
随机推荐
- CSV文件乱码处理方法
如果csv出现乱码, 直接用记事本打开另存为的格式从utf-8变为ANSI模式即可. 然后再打开
- 实验室服务器运维踩坑o.0
先说背景:实验室新配了一台Dell T640服务器,双3090, 512G内存, 5 x 8T硬盘(RAID5),2 x 1T固态(RAID1),配置很够用但就是搭建运维踩了很多坑,以下是主要完成的几 ...
- 解决ubuntu18环境matplotlib无法正常显示中文
首先看看系统装了中文字体没?命令: fc-list :lang=zh 如果没安装,需要去下载或者从win复制一份到ubuntu, 在/usr/share/fonts文件夹下创建一个chinese文件夹 ...
- MySQL 5.7升级8.0过程(详解)
记一次MySQL 5.7升级8.0的详细过程,聊聊我的思路,希望可以帮助大家. 以一个例子为切入点 一.升级背景 为什么要升级到MySQL8.0?大概多久进行一次? 大家可以参考下图记录的各个版本的发 ...
- linux 查询目录文件大小
- Python自动化测试更新selenium的两种方式
第一种手动实现: 来源 https://www.codeleading.com/article/73395290617/ import os import re import winreg impor ...
- 01、kafka常用命令
001.kafka版本 kafka_2.13-3.0.0 kafka_2.12-2.8.0 002.模拟给topic名称是 yikuang 的发一条数据(hello world) ./kafka-co ...
- “Can't open file for writing”或“operation not permitted”的解决办法
linux使用vi命令修改一个文件内容的时候,发现无法保存,每次写完使用":q!"命令可以正常退出但是使用":wq!"命令保存文件并退出时出现一下信息提示: ...
- OSS管理文件(Java)
工具类 package com.panchina.util; import com.alibaba.druid.util.StringUtils; import com.aliyun.oss.Http ...
- calibredrv命令
flattencell: set L1 [layout create *.gds -dt_expand] $L1 flatten cell TOP_CELL_NAME $L1 gdsout ./*_f ...