Numpy实现多项式曲线拟合

这里可以对比matlab中的拟合方式看看matlab拟合函数的三种方法，和第一种方式很像

问题定义：
对于一堆数据点(x, y)，能否只根据这些数据，找出一个函数，使得函数画出来的曲线和原始数据曲线尽量匹配？

多项式拟合问题：
任何可微连续的函数，都可以用一个N次多项式来估计，而比N次幂更高阶的部分为无穷小可以忽略不计

3次多项式即：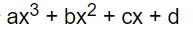

比如我们可以让sin(x) 约等于：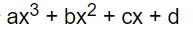

1. 构造原始数据

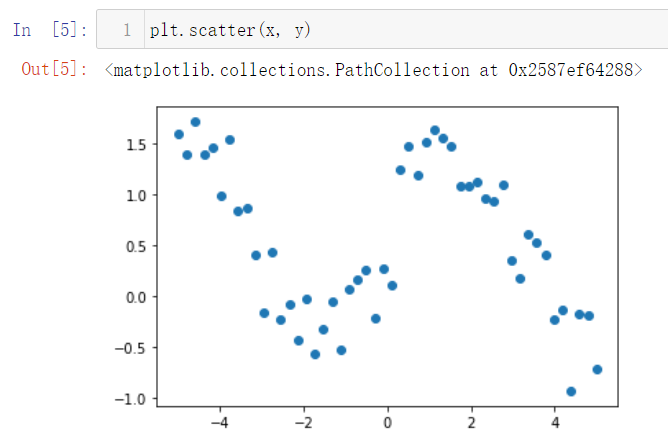
2. 使用Numpy拟合

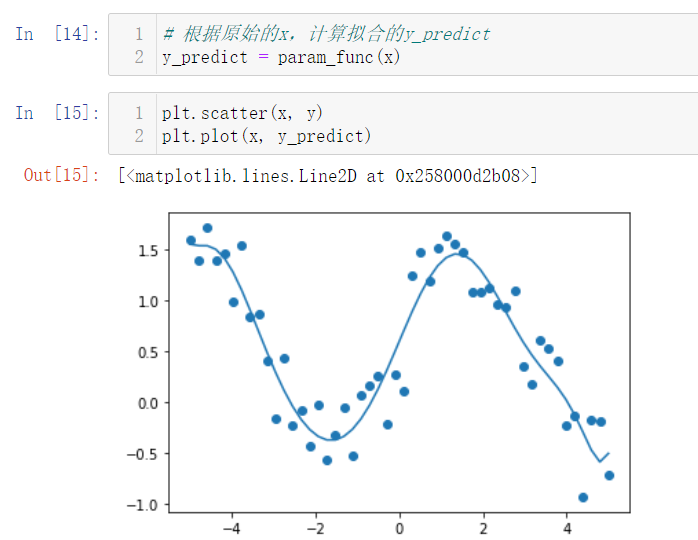
Numpy实现多项式曲线拟合的更多相关文章

  1. 最小二乘法多项式曲线拟合原理与实现 zz

    概念 最小二乘法多项式曲线拟合,根据给定的m个点,并不要求这条曲线精确地经过这些点,而是曲线y=f(x)的近似曲线y= φ(x). 原理 [原理部分由个人根据互联网上的资料进行总结,希望对大家能有用] ...

  2. Apache Commons Math3学习笔记（2） - 多项式曲线拟合(转)

    多项式曲线拟合:org.apache.commons.math3.fitting.PolynomialCurveFitter类. 用法示例代码: // ... 创建并初始化输入数据: double[] ...

  3. polyfit 多项式曲线拟合matlab

    polyfit 多项式曲线拟合 全页折叠 语法 p = polyfit(x,y,n) [p,S] = polyfit(x,y,n) [p,S,mu] = polyfit(x,y,n)   说明 示例 ...

  4. 一起啃PRML - 1.1 Example: Polynomial Curve Fitting 多项式曲线拟合

    一起啃PRML - 1.1 Example: Polynomial Curve Fitting @copyright 转载请注明出处 http://www.cnblogs.com/chxer/ 前言: ...

  5. 数据拟合：多项式拟合polynomial curve fitting

    http://blog.csdn.net/pipisorry/article/details/49804441 常见的曲线拟合方法 1.使偏差绝对值之和最小 2.使偏差绝对值最大的最小       3 ...

  6. numpy常用函数学习

    目录numpy常用函数学习点乘法线型预测线性拟合裁剪.压缩和累乘相关性多项式拟合提取符号数组杂项点乘法该方法为数学方法,但是在numpy使用的时候略坑.numpy的点乘为a.dot(b)或numpy. ...

  7. matlab 曲线拟合

    曲线拟合(转载:http://blog.sina.com.cn/s/blog_8e1548b80101c9iu.html) 补:拟合多项式输出为str 1.poly2str([p],'x') 2. f ...

  8. Matlab学以致用 - 曲线拟合

    曲线拟合 使用Matlab自带的polyfit函数,可以很方便地根据现有样本数据进行多项式曲线拟合,为了有直观感受,先上例程,如下所示: x = -:; % 样本数据x坐标 y = *x.^ + *x ...

  9. 基于MATLAB的多项式数据拟合方法研究-毕业论文

    摘要:本论文先介绍了多项式数据拟合的相关背景,以及对整个课题做了一个完整的认识.接下来对拟合模型,多项式数学原理进行了详细的讲解,通过对文献的阅读以及自己的知识积累对原理有了一个系统的认识.介绍多项式 ...

随机推荐

  1. Java课程设计---索引

    一.基础配置 ============================================================== 1.Java课程设计---Eclipse基本环境配置 2.J ...

  2. 用RecyclerView实现水平滚动和网格视图

    建立RecyclerViewActivity.java文件 1 public class RecyclerViewActivity extends AppCompatActivity { 2 priv ...

  3. 操作Jexus

    jws.start等命令在Jexus V5.6.3中已经合并为一个单一命令,即"jws",这是一个shell脚本文件. 命令参数与对应的功效: jws start : 启动Jexu ...

  4. Python迭代器,生成器,装饰器

    迭代器 通常来讲从一个对象中依次取出数据,这个过程叫做遍历,这个手段称为迭代(重复执行某一段代码块,并将每一次迭代得到的结果作为下一次迭代的初始值). 可迭代对象(iterable):是指该对象可以被 ...

  5. xxl-job踩坑记录——执行器，执行10分钟自动失败

    问题描述 上一篇Docker 部署xxl-job 报错:xxl-rpc remoting error(connect timed out), for url : xxxxxx - 这行代码没Bug - ...

  6. SQL基础语法_张三

    1.1 建库表语法 1.2 字段数据类型 大致可以分为三类:数值.日期/时间和字符串 (字符)类型. 2. 增删查改 3. 关联查询 4. 子查询

  7. ASP.NET Core框架探索之Authorization

    今天我们一起来探索一下ASP.NET Core框架中的Authorization.我们知道请求进入管道处理流程先会使用Authentication进行用户认证,然后使用Authorization进行用 ...

  8. 关于 Linux Polkit 权限提升漏洞(CVE-2021-4034)的修复方法

    镜像下载.域名解析.时间同步请点击阿里云开源镜像站 近日,国外安全团队披露了 Polkit 中的 pkexec 组件存在的本地权限提升漏洞(CVE-2021-4034),Polkit 默认安装在各个主 ...

  9. 4月27日 python学习总结 GIL、进程池、线程池、同步、异步、阻塞、非阻塞

    一.GIL:全局解释器锁 1 .GIL:全局解释器锁 GIL本质就是一把互斥锁,是夹在解释器身上的, 同一个进程内的所有线程都需要先抢到GIL锁,才能执行解释器代码 2.GIL的优缺点: 优点:  保 ...

  10. php的魔术函数和魔术常量

    0x00 魔术函数 1. __construct() 实例化对象时被调用, 当__construct和以类名为函数名的函数同时存在时,__construct将被调用,另一个不被调用. 2. __des ...