tensorflow中常用激活函数和损失函数

激活函数

各激活函数曲线对比

常用激活函数：

tf.sigmoid()

tf.tanh()

tf.nn.relu()

tf.nn.softplus()

tf.nn.softmax()

tf.nn.dropout()

tf.nn.elu()

import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative

def sigmoid(x):
    y = 1 / (1 + np.exp(-x))
    return y

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x)+np.exp(-x))

def relu(x):
    return [max(xi,0) for xi in x]

def elu(x,a=1):
    y = []
    for xi in x:
        if xi >= 0:
            y.append(xi)
        else:
            y.append(a*(np.exp(xi)-1))
    return y

def softplus(x):
    return np.log(1+np.exp(x))

def derivative_f(func,input,dx=1e-6):
    y = [derivative(func,x,dx) for x in input]
    return y

x = np.linspace(-5,5,1000)

flg = plt.figure(figsize=(15,5))
ax1 = flg.add_subplot(1,2,1)
ax1.axis([-5,5,-1,1])
plt.xlabel(r'active function',fontsize=18)
ax1.plot(x,sigmoid(x),'r-',label='sigmoid')
ax1.plot(x,tanh(x),'g--',label='tanh')
ax1.plot(x,relu(x),'b-',lw=1,label='relu')
ax1.plot(x,softplus(x),'y--',label='softplus')
ax1.plot(x,elu(x),'b--',label='elu')
ax1.legend()
ax2 = flg.add_subplot(1,2,2)
plt.xlabel(r'derivative',fontsize=18)
ax2.plot(x,derivative_f(sigmoid,x),'r-',label='sigmoid')
ax2.plot(x,derivative_f(tanh,x),'g--',label='tanh')
ax2.plot(x,derivative_f(softplus,x),'y-',label='softplus')
ax2.legend()
plt.show()

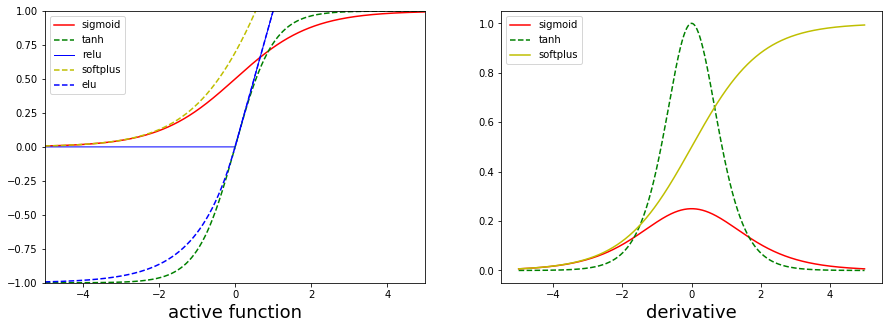
各激活函数优缺点

sigmoid函数

优点：在于输出映射在（0，1）范围内，单调连续，适合用作输出层，求导容易

缺点：一旦输入落入饱和区，一阶导数接近0，就可能产生梯度消失的情况

tanh函数

优点：输出以0为中心，收敛速度比sigmoid函数要快

缺点：存在梯度消失问题

relu函数

优点：目前最受欢迎的激活函数，在x<0时，硬饱和，在x>0时，导数为1，所以在x>0时保持梯度不衰减，从而可以缓解梯度消失的问题，能更快收敛，并提供神经网络的稀疏表达能力

缺点：随着训练的进行，部分输入或落入硬饱和区，导致无法更新权重，称为‘神经元死亡’

elu函数

优点：有一个非零梯度，这样可以避免单元消失的问题

缺点：计算速度比relu和它的变种慢，但是在训练过程中可以通过更快的收敛速度来弥补

softplus函数

该函数对relu做了平滑处理，更接近脑神经元的激活模型

softmax函数

除了用于二分类还可以用于多分类，将各个神经元的输出映射到（0,1空间）

dropout函数

tf.nn.dropout(x,keep_prob,noise_shape=None,seed=None,name=None)

一个神经元以概率keep_prob决定是否被抑制，如果被抑制，神经元的输出为0，如果不被抑制，该神经元将被放大到原来的1/keep_prob倍，默认情况下，每个神经元是否被抑制是相互独立的

一般规则

当输入数据特征相差明显时，用tanh效果很好，当特征相差不明显时用sigmoid效果比较好，sigmoid和tanh作为激活函数需要对输入进行规范化，否则激活后的值进入平坦区，而relu不会出现这种情况，有时也不需要输入规范化，因此85%-90%的神经网络会使用relu函数

损失函数

sigmoid_cross_entropy_with_logits函数

tf.nn.sigmoid_cross_entropy_with_logits(_sentinel=None,labels=None,logits=None)

该函数不仅可以用于二分类，也可以用于多分类，例如：判断图片中是否包含几种动物中的一种或多种

二分类logstic损失函数梯度推导

二项逻辑斯蒂回归模型是一种分类模型，由条件概率p(y|x)表示，形式未参数化的逻辑斯蒂分布，这里的变量X为实数，随机变量y取值为1或0，逻辑斯蒂模型条件概率分布如下：$$p(y=1|x) = \frac{\exp(w{\bullet}x+b)}{1+\exp(w{\bullet}x+b)}$$

\[p(y=0|x) = \frac{1}{1+\exp(w{\bullet}x+b)}
\]

假设$$p(y = 1|x) = \theta(x),p(y=0|x) = 1 - \theta(x)$$

损失函数：$$L(\theta(x)) = -\prod_{i=1}^{N[\theta(x_i)]}{y_i}[1-\theta(x_i)]^{1-y_i}$$

对数似然函数：$$L(\theta(x)) = -\sum_{i=1}^Ny_i * \log\theta(x_i)+(1-y_i)\log(1-\theta(x_i))$$

求\(L(\theta(x))\)的极大值，得到w的估计值,由于\(L(\theta(x))\)为凸函数，可以直接求损失函数的一阶偏导：

\[\frac{\delta{L}}{\delta{w_j}} = -\sum_{i=1}^N[y_i*\frac{1}{\theta(x_i)} - (1-y_i)*\frac{1}{1-\theta(x_i)}] *\frac{\delta{\theta(x)}}{\delta{w_j}}
\]

由于\(\frac{\delta{\theta(x)}}{\delta{w}} = \theta(x_i) * (1 - \theta(x_i))*x_j^i\)

得到：$$\frac{\delta{L}}{\delta{w_j}} = -\sum_{i=1}^{N(y_i-\theta(x_i))*x_j}i$$

weighted_cross_entropy_with_logits函数

tf.nn.weighted_cross_entropy_with_logits(targets,logits,pos_weight,name=None)

pos_weight正样本的一个系数

该函数在sigmoid_cross_entropy_with_logits函数的基础上为每个正样本添加了一个权重，其损失函数如下：

\[loss_{ij} = -[post_{weight}p_{ij}\log p_{ij}+(1-p_{ij})\log (1-p_{ij})]
\]

softmax_cross_entropy_with_logits函数

tf.nn.softmax_cross_entropy_with_logits(_sentinel,labels,logits,name)

适用于每个类别相互独立且排斥的情况，例如，判断的图片只能属于一个种类而不能同时包含多个种类

损失函数：

\[logits_{ij} = \frac{e^{logits_{ij}}}{\sum_{j=0}^{numclass-1}e^{logits_{ij}}}
\]

\[loss_{i} = -\sum_{j=0}^{numclass-1}label_{ij}\log (logits_{ij})
\]

sparse_softmax_cross_entropy_with_logits函数

tf.nn.sparse_softmax_cross_entropy_with_logits(_sentinel,labels,logits,name)

该函数与softmax_cross_entropy_with_logits的唯一区别在于labels,该函数的标签要求排他性的即只有一个正确类型，labels的形状要求是[batch_size]而值必须是从0开始编码的int32或int64，而且范围是[0,num_class]，该函数没用过