Vim配置Node.js开发工具

1. ubuntu安装vim编辑器。默认情况下，vim在运行的时候会加载～/.vimrc文件里的配置文件，如果在～目录下不存在这个配置文件可以手动创建。
2. 在～/.vim目录下是vim的插件加载的位置，可以在这个文件夹下放置多个插件。
3. 首先安装一个vim插件的管理器pathogen插件。我们按照常规把pathogen.vim安装在autoload文件夹下，这样vim就会自动加载插件的时候找到pathogen，然后我们把其余的插件都安装在bundle文件夹下，由pathogen路由给vim。配置如下

   harvey@harvey:~/.vim$ mkdir -p ~/.vim/autoload ~/.vim/bundle #创建安装vim插件的文件夹bundle和antoload
   harvey@harvey:~/.vim$ ls ~/.vim #查看结果
   autoload   bundle  
   
   harvey@harvey:~/.vim$ git clone https://github.com/tpope/vim-pathogen.git #从git上同步下来pathogen项目
   Cloning into 'vim-pathogen'...
   remote: Reusing existing pack: 501, done.
   remote: Counting objects: 4, done.
   remote: Compressing objects: 100% (3/3), done.
   remote: Total 505 (delta 0), reused 0 (delta 0)
   Receiving objects: 100% (505/505), 85.89 KiB | 35.00 KiB/s, done.
   Resolving deltas: 100% (146/146), done.
   Checking connectivity... done
   harvey@harvey:~/.vim$ ls
   autoload  bundle  vim-pathogen
   harvey@harvey:~/.vim$ tree vim-pathogen #查看文件结构如下
   vim-pathogen
   |-- CONTRIBUTING.markdown
   |-- README.markdown
   `-- autoload
       `-- pathogen.vim
   
   1 directory, 3 files
   harvey@harvey:~/.vim$ mv vim-pathogen/autoload/pathogen.vim autoload/ #把pathogen.vim移动到autoload文件夹下

   到此，pathogen安装完毕，我们需要配置文件，因为是第一个配置~/.vimrc。所有配置文件统一在下面粘贴。插件网址：https://github.com/tpope/vim-pathogen

4. NerdTree是可以查看当前工作的目录和子目录的tree结构

   cd ~/.vim/bundle
   git clone https://github.com/scrooloose/nerdtree.git

   直接用：:NERDTree就可以打开这个工具栏。但是为了安装使用方法 我们使用nmap <f2>  :NERDTree配置快捷键 可以用?查看帮助

5. 安装node.js插件

   cd  ~/.vim/bundle
   git clone https://github.com/moll/vim-node.git ~/.vim/bundle/node

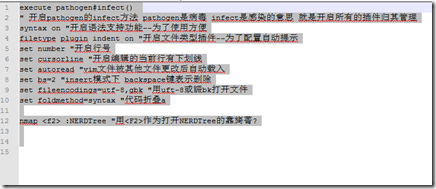
配置文件：