【大杀器】利用划分树秒杀区间内第k大的数

　　最近看了一道题，大概就是给出一个序列，不断询问其子区间内第k大的数，下面是个截图

　　绕了一圈没找到中文版题目，if（你是大佬） then 去看截图；else{我来解释：给出一个整数n，和一个整数m，分别表示序列元素个数和询问次数，然后输入n个数和m个询问，每个询问包含3个数，分别是区间起止点（l和r）和k，求出区间内第k大的数并输出；}这是一道很简单的模板题，怎么解决呢？小编最初想到的是打暴力，正所谓暴力出奇迹，说不定可以成功，反正不会优化，先试试吧，直接把规定区间[l,r]排一次序了，然后在查找一遍第k大的数，但是毫无疑问，绝对会超时，怎样能减少时间复杂度呢？这是就请出了二分。

　　二分运用了分治的思想，不断将子区间分成两半，直到找到第k大的数，虽然很高效，但是面对这道题的多次询问，二分也只能表示手软，仍然过不了这道题。但是如果换成了线段树的结构，效率则会快很多，线段树看起来也用了分治的思想，把原来的整个序列都大约相等的长度分到左子树和右子树，不断分下去，直到全部分成叶子节点，在逐次确定下一层第k大的数在左子树还是右子树，虽然这种树能成功AC，但是并不是最优的，做题不能只讲求AC，下面就来讲一讲线段树的升级版——划分树。

什么是划分树？

　　划分树是一种基于线段树的数据结构，也利用了分治的思想，却比线段树高效很多，这是为什么？因为划分树又多了一个性质：在划分时不是随意划分，也不是排序后直接划分（因为这样会破坏原有结构），而是排序后仍保持原来的相对顺序再分到左右子树。

具体实现方法：

　　整个过程分为建树和查询两个阶段：

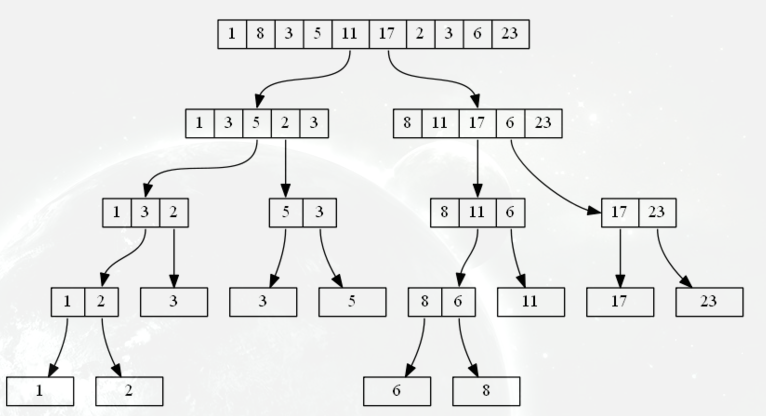
//copy来的图

1）建树：首先定义一个数组tree[30][1000]第一个维度表示层数，第二个维度表示这一层第i个数的值，用来表示这棵划分树，然后定义sorted[1000]数组，用来存储排序好的原序列，然后记录每一层前i个数有多少进入了下一层的左子树，存在toleft[30][1000]数组中，在建树中没用，但记录下来对查找时有用，用分治的思想分配左子树和右子树，将不大于中间值mid的数分配到左子树中去，大于中间值的分配到右子树中去，但有时为了左右尽可能个数相等，要把等于中间值的数两边都分配，于是定义same来存储多少等于中间值的数进入左子树，分配完毕后再递归分配左子树和右子树。身为递归，怎么也要有个出口吧，递归到叶子节点时就返回，即if（l==r） return；

2）查询：按照之前存储下的进入下一层左子树个数的数组toleft，可以计算出区间内第k大的数在当前节点的左子树还是右子树，并计算出下一层相应子树的左右边界，然后递归相应子树，同上，递归出口也是到达叶子节点时返回。详见注释……

废话不多说，代码呈上：

#include<iostream>
#include<algorithm>
using namespace std;
int tree[][],sorted[],toleft[][],n,m,ans;//tree和toleft的两个维度分别存储深度和序列，sorted存储的是排序好的序列
void buildtree(int l,int r,int dep)//构建划分树
{
    if(l==r) return;//遇见叶子节点就返回
    int mid=(l+r)/;//二分
    int same=mid-l+;//same最终保存的是和中间值相同元素的个数，以便确定分到哪一区间
    for(int i=l;i<=r;i++)
    if(tree[dep][i]<sorted[mid]) same--;
    int lpos=l;int rpos=mid+;//左指针和右指针，并非常用的指针，是用来保存现在各区间内元素个数
    for(int i=l;i<=r;i++)
    {
        if(tree[dep][i]<sorted[mid])//小于中间值
        tree[dep+][lpos++]=tree[dep][i];//分配到左子区间
        else if(tree[dep][i]==sorted[mid]&&same>)//等于中间值且相同个数大于0
        {
            same--;
            tree[dep+][lpos++]=tree[dep][i];//分配到右子区间
        }
        else tree[dep+][rpos++]=tree[dep][i];//剩下的分配到右子区间
        toleft[dep][i]=toleft[dep][l-]+lpos-l;//toleft数组记录这一层前i个数有多少个进入下一层的左子区间，查询时有用
    }
    buildtree(l,mid,dep+);//构建左子区间（左子树）
    buildtree(mid+,r,dep+);//构建右子区间（右子树）
}
int search(int L,int R,int l,int r,int dep,int k)//查询第k大的数
{
    if(l==r) return tree[dep][l];//查询到符合要求的叶子节点，返回相应的值
    int mid=(L+R)/;//L,R为大区间（主要是每个左子树，右子树的边界）
    int cnt=toleft[dep][r]-toleft[dep][l-];//求出[l,r]区间内有多少数进入下一层左子区间
    if(cnt>=k)//第k大的数对应节点在左子树
    {
        int newl=L+toleft[dep][l-]-toleft[dep][L-];//求出下一层第k大的数所在区间边界
        int newr=newl+cnt-;
        return search(L,mid,newl,newr,dep+,k);
    }
    else//在右子树
    {
        int newr=r+toleft[dep][R]-toleft[dep][r];//求出下一层第k大的数所在区间边界
        int newl=newr-(r-l-cnt);
        return search(mid+,R,newl,newr,dep+,k-cnt);
    }
}
int main()
{
    cin>>n>>m;
    for(int i=;i<=n;i++)
    {
        cin>>tree[][i];
        sorted[i]=tree[][i];
    }
    sort(sorted+,sorted+n+);//为sorted数组排序
    buildtree(,n,);//建树
    int a,b,c;
    for(int i=;i<=m;i++)
    {
        cin>>a>>b>>c;//输入询问
        cout<<search(,n,a,b,,c)<<endl;//查询第k大的数
    }
    return ;
}

//额~好像忘了改scanf和printf了，没过别怪我……