[CSP-S模拟测试]:x（数学+并查集）

题目背景

$\frac{1}{4}$遇到了一道水题，叒完全不会做，于是去请教小$D$。小$D$都没看就切掉了这题，嘲讽了$\frac{1}{4}$一番就离开了。于是，$\frac{1}{4}$只好来问你，这道题是这样的：

---

题目描述

给定一个长度为$n$的正整数序列$\{a_i\}$。
将$\{1,2,...,n\}$划分成两个非空集合$S$、$T$，使得$gcd(\prod_{i\in S}a_i,\prod_{i\in T}a_i)=1$。
求划分方案数，对$10^9+7$取模。

---

输入格式

从文件$x.in$中读入数据。
第一行，一个非负整数$t$，代表数据组数。
每组数据的第一行，一个正整数$n$。
第二行，$n$个正整数，代表$\{a_i\}$。

---

输出格式

输出到文件$x.out$中。
输出$t$行，每行一个非负整数，代表答案对$10^9+7$取模的结果。

---

样例

样例输入：

3
3
2 3 1
3
2 3 6
4
2 3 6 1

样例输出：

6
0
2

---

数据范围与提示

样例解释：

$\bullet$第$1$组数据，任意一种非空集合划分均满足。
$\bullet$第$2$组数据，任意一种非空集合划分均不满足。
$\bullet$第$3$组数据，$S=\{1,2,3\},T=\{4\},gcd(a_1\times a_2\times a_3,a_4)=1$，或者$S=\{4\},T=\{1,2,3\},gcd(a_4,a_1\times a_2\times a_3)=1$。

数据范围：

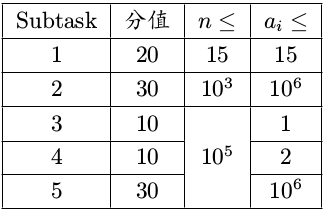
保证，$0\leqslant t\leqslant 5,1\leqslant n\leqslant 10^5,1\leqslant a_i\leqslant 10^6$。

---

题解

似乎有一个很显然的性质：$gcd\neq 1$的连边，连通块个数为$cnt$，那么答案为$2^{cnt}−2$。

然而我考场上却没有想出来，想了一晚上才想明白，但是好多人都觉得这很显然，智商还是硬伤哇……

其他的没啥说的了，并查集维护一下联通块数就好了。

时间复杂度：$\Theta(1000000\times k)$（$k$为很小的常数）。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
const int mod=1000000007;
int n;
int a[100001],fa[100001];
int que[80000],lst[80000];
bool v[1000001],vis[1000001];
long long ans;
vector<int> prime[1000001];
void pre_work()
{
	ans=0;
	memset(lst,0,sizeof(lst));
	memset(vis,0,sizeof(vis));
	for(int i=1;i<=n;i++)fa[i]=i;
}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
void get_prime()
{
	for(int i=2;i<=1000000;i++)
	{
		if(v[i])continue;que[++que[0]]=i;
		for(int j=i;j<=1000000;j+=i)
		{
			v[j]=1;
			prime[j].push_back(que[0]);
		}
	}
}
long long qpow(long long x,long long y)
{
	long long res=1;
	while(y)
	{
		if(y&1)res=res*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return res;
}
int main()
{
	get_prime();
	int T;scanf("%d",&T);
	while(T--)
	{
		scanf("%d",&n);
		pre_work();
		for(int i=1;i<=n;i++)scanf("%d",&a[i]);
		for(int i=1;i<=n;i++)
			for(int j=0;j<prime[a[i]].size();j++)
				if(!lst[prime[a[i]][j]])lst[prime[a[i]][j]]=i;
				else fa[find(i)]=find(lst[prime[a[i]][j]]);
		for(int i=1;i<=n;i++)
			if(!vis[find(i)])
			{
				vis[find(i)]=1;
				ans++;
			}
		printf("%lld\n",(qpow(2,ans)-2+mod)%mod);
	}
	return 0;
}

---

rp++