【HDU6609】Find the answer【线段树】

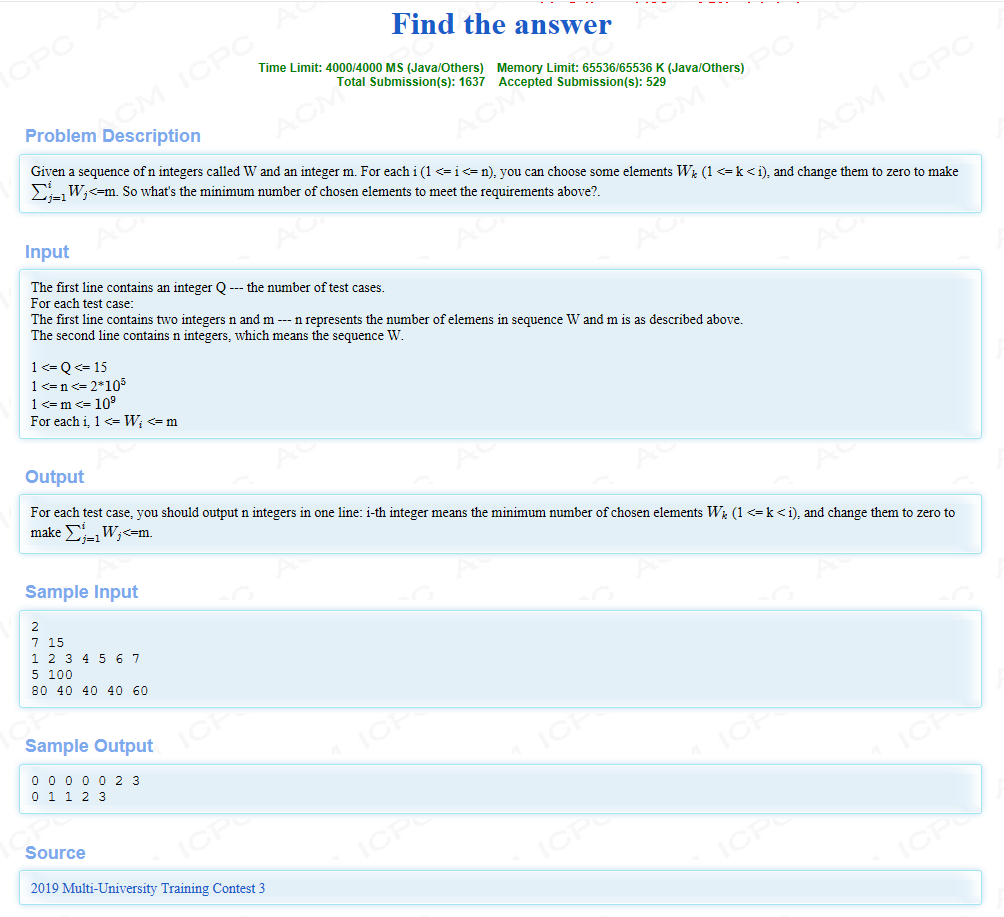
题目大意：给你一个序列，对于每个i，你可以选择1~i-1中任意多的数并将它删去，剩余的数（包括i）∑≤m，问对于每个i最少删几个数可以达到要求

题解：

考虑朴素的思想，对于每个i，我只需要删去最大的若干个使得∑≤m即可，时间复杂度O(n^2)

显然不可接受，考虑优化

显然可以看出，因为只需要删去最大的若干数，于是想到前K大，于是很自然想到用线段树

先离散化，只需要记录这个数是第几大，之后线段树维护区间和，每新加入一个点时加入这个点第几大的下标

询问时在线段树上二分出前K大即可，时间复杂度O(nlogn)

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<string>
#define ll long long
using namespace std;
int TT,n;
int ans[];
ll m;
struct node
{
    ll v;
    int bh,rk;
}a[];
bool cmp(const node &T1,const node &T2){return T1.v<T2.v;}
bool cmp2(const node &T1,const node &T2){return T1.bh<T2.bh;}
ll sum[*],cnt[*];
int ask(int l,int r,ll v,int pos,ll tot)
{
    if(sum[pos]+tot<=v)return cnt[pos];
    else
    {
      int mid=l+r>>;
      int t=ask(l,mid,v,pos<<,tot);
      if(t==cnt[pos<<])t+=ask(mid+,r,v,pos<<|,tot+sum[pos<<]);
      return t;
    }
}
void insert(int l,int r,ll v,int p,int pos)
{
    if(l==r && l==p)
    {
      sum[pos]=v;cnt[pos]=;
      return;
    }
    int mid=l+r>>;
    if(p<=mid)insert(l,mid,v,p,pos<<);
    else insert(mid+,r,v,p,pos<<|);
    sum[pos]=sum[pos<<]+sum[pos<<|];
    cnt[pos]=cnt[pos<<]+cnt[pos<<|];
}
int main()
{
    scanf("%d",&TT);
    while(TT--)
    {
      memset(sum,,sizeof(sum));
      memset(cnt,,sizeof(cnt));
      memset(ans,,sizeof(ans));
      scanf("%d%lld",&n,&m);
      for(int i=;i<=n;i++){scanf("%lld",&a[i].v);a[i].bh=i;}
      sort(a+,a++n,cmp);
      for(int i=;i<=n;i++)a[i].rk=i;
      sort(a+,a++n,cmp2);
      for(int i=;i<=n;i++)
      {
        int t=ask(,n,m-a[i].v,,);
        ans[i]=i--t;
        insert(,n,a[i].v,a[i].rk,);
      }
      for(int i=;i<=n;i++)printf("%d ",ans[i]);
      printf("\n");
    }
    return ;
}

心得：考场上很自然的想到，说明该部分知识掌握不错，继续加油