斜率优化dp学习笔记 洛谷P3915[HNOI2008]玩具装箱toy

本文为原创？？？

作者写这篇文章的时候刚刚初一毕业……

如有错误请各位大佬指正

---

从例题入手

洛谷P3915[HNOI2008]玩具装箱toy

Step0：读题

Q：暴力？

如果您学习过dp

不难推出dp方程

设dp[i]表示放置前i个物品需要的最小价值

dp[i]=min(dp[j]+(sum[i]-sum[j-1]+i-j-L)^2)

sum[i]表示前缀和

暴力分有了！！恭喜！

下面我们引入斜率优化：

首先进行一个变形：

原来的式子可以变为：f[i]=min(f[j]+(sum[i]-sum[j]+i-j-L-1)^2)

令a[i]=sum[i]+i,b[i]=sum[i]+i+L+1

f[i]=min(f[j]+(a[i]-b[j])^2)

f[i]=min(f[j]+a[i]^2+b[j]^2-2*a[i]*b[j])     初一公式！展开平方！

把b[j]看做x，f[j]+b[j]^2看做y

y=2*a[i]x+dp[i]-a[i]^2

这就是一条是直线的解析式！

y=kx+b,k=2*a[i],b=f[i]-a[i]^2

要找到一个点P(b[j],f[j]+b[j]^2)使得上面的斜率为2*a[i]的直线穿过这个点且与y 的轴截距最小

因为斜率k=2*a[i]是固定的，所以要求的就是最小的b，加上a[i]^2就是dp[i]的值。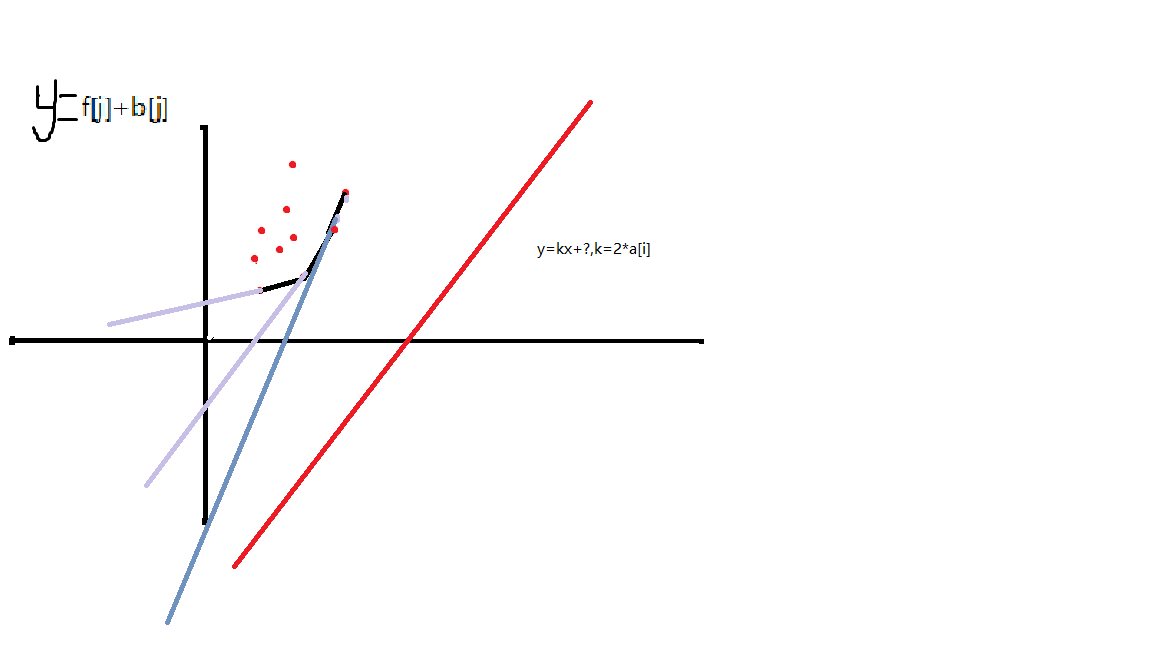

很明显就是维护一个下凸壳

令a[i]=sum[i]+i

斜率单调递增！

code：推荐照着讲解看

#include<bits/stdc++.h>
#define ll long long
#define inf 0x7fffffff
#define un unsigned
#define ull un ll
#define int ull
using namespace std;
#define maxn 50009
int n,l,a[maxn];
int f[maxn],g[maxn];
int q[maxn];
int Q(int x){return x*x;}
double Get(un j,un k)//求斜率
{
    return ((f[j]+Q(g[j])+*l*g[j])-(f[k]+Q(g[k])+*l*g[k]))/(double)(g[j]-g[k]);
}
signed main()
{
    scanf("%llu%llu",&n,&l);
    l++;
    int s=,t=;
    int K;
    q[s]=;
    for(int i=;i<=n;i++)
    {
        scanf("%llu",&g[i]);
        g[i]=g[i]+g[i-];
    }
    for(int i=;i<=n;i++)g[i]+=i;
    for(int i=;i<=n;q[++t]=i++)
    {
        K=g[i]<<;
        while(s<t&&Get(q[s+],q[s])<=K) s++;
        int j=q[s];
        f[i]=f[j]+Q(g[i]-g[j]-l);
        while(s<t&&Get(q[t],q[t-])>=Get(i,q[t]))t--;
    }
    printf("%llu\n",f[n]);
    return ;
}