【Python】机器学习之单变量线性回归 利用批量梯度下降找到合适的参数值

【Python】机器学习之单变量线性回归 利用批量梯度下降找到合适的参数值

---

本题目来自吴恩达机器学习视频。

题目：

你是一个餐厅的老板，你想在其他城市开分店，所以你得到了一些数据（数据在本文最下方），数据中包括不同的城市人口数和该城市带来的利润。第一列是城市的人口数，第二列是在这个城市开店所带来的利润数。

现在，假设一开始θ0和θ1都是0，利用梯度下降的方法，找到合适的θ值，其中学习速率α=0.01，迭代轮次为1000轮

上一个文章里，我们得出了CostFunction，即损失函数。

现在我们需要找到令损失函数最小的θ值，利用梯度下降函数

1、导包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

2、之前写的CostFunction函数

def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

3、引入文件，把X和Y分开，在X左边加一列1，θ0和θ1设置为0，0

path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])

data.insert(0, 'Ones', 1)
rows = data.shape[0]
cols = data.shape[1]
X = data.iloc[:, 0:cols - 1]
Y = data.iloc[:, cols - 1:cols]
theta = np.mat('0,0')
X = np.mat(X.values)
Y = np.mat(Y.values)

cost = computeCost(X, Y, theta)

4、设置更新速率α为0.01，设置迭代次数为1000次

alpha = 0.01
iters = 1500

5、写出梯度下降函数的实现

def gradientDescent(X, Y, theta, alpha, iters):
    temp = np.mat(np.zeros(theta.shape))  # 一个数组，temp大小为θ的个数
    parameters = int(theta.ravel().shape[1])  # 参数的个数
    cost = np.zeros(iters)  # 一个数组，存着每次计算出来的costFunction的值

    for i in range(iters):
        error = (X*theta.T)-Y;  #误差值
        for j in range(parameters):
            term = np.multiply(error,X[:, j])
            temp[0,j] = theta[0,j] - ((alpha/len(X)) * np.sum(term))
        theta = temp
        cost[i] = computeCost(X,Y,theta)
    return theta, cost

解析：

temp数组存的是临时变量，因为所有的θ需要同步更新，所以先存入临时变量中，后面计算完所有θ的值后再同步更新。

parameters是一个int值的数，即有多少个变量，本题中有θ0和θ1，所以parameters=2

cost是一个数组，大小和迭代次数一样，每一层存放当前迭代次数下的CostFunction的返回值

6、调用函数，并返回结果

g, cost = gradientDescent(X, Y, theta, alpha, iters)
print(g)

最后结果g=[[-3.24140214  1.1272942 ]]

即最后的θ0=-3.24 θ1=1.127

7、把图打出来，看看是否收敛

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters),cost,'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
plt.show()

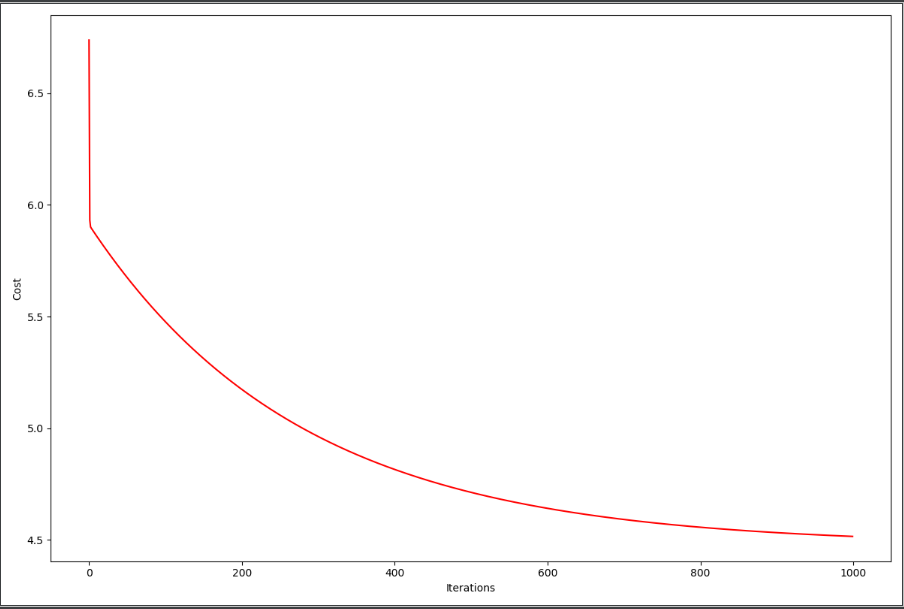
发现随着迭代次数iters的增大，损失慢慢的降低，所以有效，计算正确。

PS：数据集在机器学习的第一篇中的最下方。