JVM-GC算法(二)-复制算法&&标记整理算法

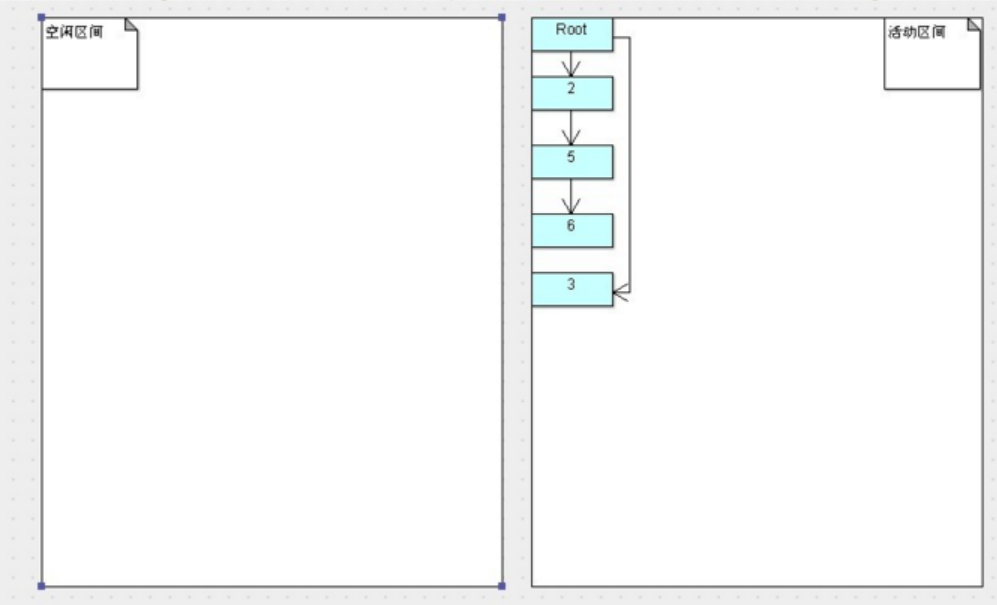

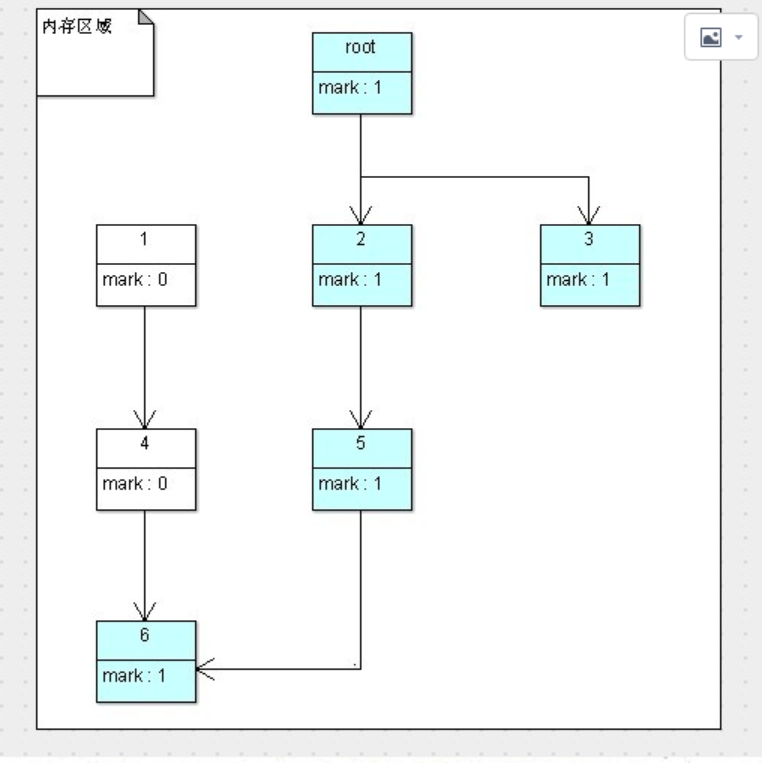

JVM-GC算法(二)-复制算法&&标记整理算法的更多相关文章
- JVM内存管理------GC算法精解(复制算法与标记/整理算法)
本次LZ和各位分享GC最后两种算法,复制算法以及标记/整理算法.上一章在讲解标记/清除算法时已经提到过,这两种算法都是在此基础上演化而来的,究竟这两种算法优化了之前标记/清除算法的哪些问题呢? 复制算 ...
- JVM内存管理之GC算法精解(复制算法与标记/整理算法)
本次LZ和各位分享GC最后两种算法,复制算法以及标记/整理算法.上一章在讲解标记/清除算法时已经提到过,这两种算法都是在此基础上演化而来的,究竟这两种算法优化了之前标记/清除算法的哪些问题呢? 复制算 ...
- JVM之GC算法、垃圾收集算法——标记-清除算法、复制算法、标记-整理算法、分代收集算法
标记-清除算法 此垃圾收集算法分为“标记”和“清除”两个阶段: 首先标记出所有需要回收的对象,在标记完成后统一回收所有被标记对象,它的标记过程前面已经说过——如何判断对象是否存活/死去 死去的对象就会 ...
- JVM 垃圾收集算法 标记-清楚、标记-复制、标记-整理
摘要 Java程序在运行过程中会产生大量的对象,但是内存大小是有限的,如果光用而不释放,那内存迟早被耗尽.如C.C++程序,需要程序员手动释放内存,Java则不需要,是由垃圾回收器去自动回收. 垃圾回 ...
- JVM垃圾收集算法(标记-清除、复制、标记-整理)
[JVM垃圾收集算法] 1)标记-清除算法: 标记阶段:先通过根节点,标记所有从根节点开始的对象,未被标记的为垃圾对象(错了吧?) 清除阶段:清除所有未被标记的对象 2)复制算法: 将原有的内存空间 ...
- <转>GC其他:引用标记-清除、复制、标记-整理的说明
注:本文根据<深入理解Java虚拟机>第3章部分内容整理而成. 对象死亡历程 1.基本的mark&sweep是必须的,后续的都是对他的改进, 2.young代理的survivor就 ...
- GC其他:引用标记-清除、复制、标记-整理的说明
对象死亡历程 1.基本的mark&sweep是必须的,后续的都是对他的改进, 2.young代理的survivor就是使用了复制算法,避免碎片 3.还有标记整理算法(压缩),就是将存活的对象移 ...
- JVM-GC算法(一)-标记清除算法
首先,我们得知道根搜索算法,它可以解决我们应该回收哪些对象的问题,但是它显然还不能承担垃圾搜集的重任,因为我们在程序(程序也就是指我们运行在JVM上的JAVA程序)运行期间如果想进行垃圾回收,就必须让 ...
- JVM GC算法
在判断哪些内存需要回收和什么时候回收用到GC 算法,本文主要对GC 算法进行讲解. JVM垃圾判定算法 常见的JVM垃圾判定算法包括:引用技术算法.可达性分析算法. 引用技术算法(Reference ...
随机推荐
- MVC4学习要点记四
一.使用原生SQL使用EF的一个优点就是自动帮我们生成SQL,这在常规情况下很方便,但有些情况下用EF却不适合.另外还有些特别复杂的语句,利用EF很难生成.所以,EF提供一组方法用来执行原生的SQL. ...
- ZROI-Day2比赛解题报告
ZROIDay2-比赛解题报告 版权原因不提供题面信息 序 这几天作息有点鬼畜,虽然昨晚很晚睡但是早上精神还不错,看到题发现T1很友好?T2woc这暴力都好难打?T3多项式?!这样下去比赛会不会出现更 ...
- QT编译Mysql驱动问题及解决方案
默认情况下,qt 并没有自带mysql的数据库插件,需要自己编译先安装mysql server ,运行setup.exe时选择自定义安装,安装目录设为"D:\mysqldev"不要 ...
- maven简识
https://www.cnblogs.com/whgk/p/7112560.html 一:命令行管理maven项目: 创建maven[java]项目: D:\maven\demo>mvn ar ...
- ui组件库
基于Vue的Quasar Framework 中文网 http://www.quasarchs.com/ quasarframework/quasar: Quasar Frameworkhttps:/ ...
- Redis-String常用命令
Redis-String常用命令 set key value- 设置Key-value键值对 get key 获取指定key对应的值 append key value 在指定key对应值的后面追加va ...
- Delphi 10.3.2试用报告
感谢朋友们,如此之快就发了注册机,209321818群里有下载,感兴趣可以去. 安装前,需要先卸载Delphi 10.3.1,然后就是正常的安装过程,非常顺利,现在差不多半小时就安装完成. 安装后,启 ...
- thinkphp5.0 column多字段问题
一个字段:返回一维数组,数字索引为键名: 二个字段:返回一维数组,第一个字段为键名,第二个字段为元素值: 三个或更多字段:返回二维数组,第一个字段为键名,全部字段值为数据元素: 指定键名:方法的第二个 ...
- linux基础—课堂随笔05_文本三剑客之SED
1.简介 sed是非交互式的编辑器,它不会修改文件,除非使用shell重定向来保存结果.默认情况下,所有的输出行都被打印到屏幕上. sed编辑器逐行处理文件(或输入),并将结果发送到屏幕.具体过程如下 ...
- shell脚本基础和grep文本处理工具企业应用3
文本处理工具: linux上文本处理三剑客 grep,egrep,fgrep:文本过滤工具(模式:pattern)工具 grep:默认支持的是基本正则表达式: ...
