STL源码剖析 - RB-tree

在我看来，看源码是一件既痛苦又兴奋的事。当我们在推敲其中的难点时，是及其痛苦的，但当发现实现代码是那么丝滑简洁时，“wc， nb!”。

---

1. 导语

如果我们去看关联式容器map、set、multimap、multiset源代码，我们发现绝大部分操作如插入、修改、删除、搜索，均是由其内含的红黑树来完成的，我们有必要去揭开她的神秘面纱，一览她的绝世风姿。

（如果你手头还没有《STL源码剖析》时，强烈建议你现在就去买一本or文末的百度云链接or网路上的其他资源）

关键词：RB-tree、BST、AVL tree 、STL Sources

---

 从哪里讲起呢？

二叉搜索树，每个节点最多有两个子节点，而每个节点键值一定大于左子树键值节点键值，而小于右子树节点键值。这样一来，就可以提供对数时间的插入和搜索。

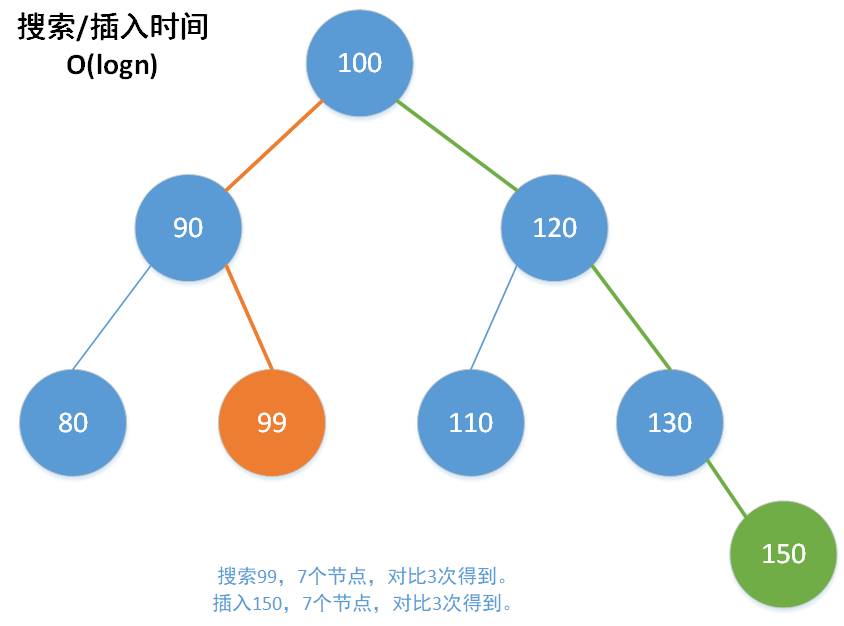
当然，较为复杂的是它的删除操作。

1.如果删除的是叶子，那么直接删除delete该指针即可；

2. 如果删除的不是叶子，而他只有一个节点，那么就将其子节点连至它的父节点；

3. 如果删除的不是叶子，而他有两个节点，那么就用它的右子树的最小节点代替他（值赋给它），删除该右子树最小节点。

（这是为什么？因为删除之后还要保证二叉树的搜索，所以替代他的元素就需要是比他大的下一个元素，而比他大的元素都在右子树，且最小的哪一个就是最左边的那一个。其实在二叉搜索树中，要找最大就一直向右子树找，要找最小就一直往左子树找）

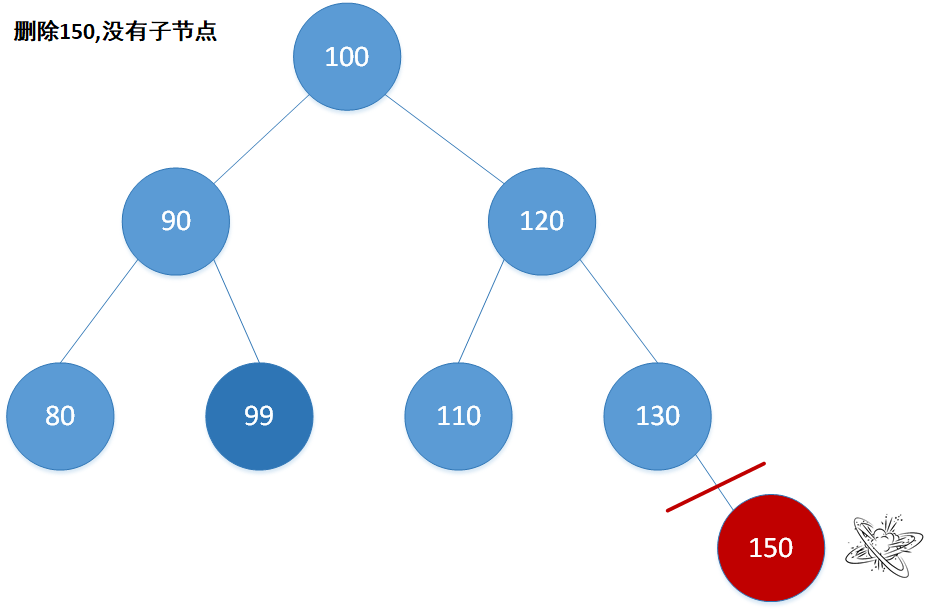
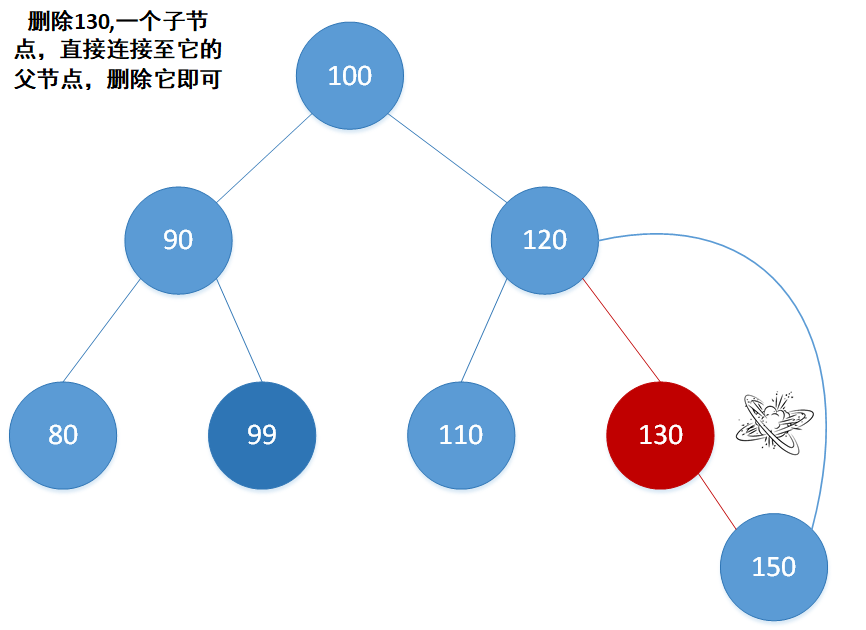
　　上述例子是在二叉树平衡的情况下进行的。平衡即左右子树高度相近，完全平衡则要求左右子树高度（深度/层数）完全相等。要是完全平衡的条件下，我们的搜索和插入操作就会是对数时间，这无疑是相当快的（当然比起Hashtable的大致O(1)来说是较慢的），这在关联式容器中是我们所追求的。因为它们的底层均不是线性结构，能达到常数时间的查找/搜索。

　　但是要知道，维护一个二叉树的完全平衡是非常耗时的，比如我插入之后，很大概率就会使得二叉树不完全平衡，就需要复杂度旋转移位操作，这对于插入来说非常不划算，也就是说，我们没必要为了平衡而平衡，只要达到大致平衡，就可以得到统计上的对数查找插入时间。

那么进入我们的正题，平衡二叉搜索树。

---

2. 平衡二叉搜索树

这里的平衡，是指没有任何节点的深度过大，而非绝对的平衡。

代表结构：RB-tree、AVL-tree、AA-tree

本片主要介绍红黑树，AVL-tree将在其他篇章中讲解。

---

3. RB-tree

红黑树，一种自平衡的二叉查找树。它的最坏情况运行时间也是良好的，并且在实践中是高效的，它可以在O(log n)时间内做查找，插入和删除。（来自百度百科）

无疑，它的实现是非常复杂的，搜索几乎是是它最为简单的操作，复杂度O(log n)，最坏也是如此。而插入和删除就比较困难了，查找到插入节点/删除节点复杂度O(log n)，在插入时、插入后、删除后都需要满足它的红黑规则限定