poj1039 Pipe【计算几何】

含【求直线交点】、【判断直线与线段相交】模板

 

Pipe

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions:11940		Accepted: 3730

Description

The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe. Note that the material which the pipe is made from is not transparent and not light reflecting. 

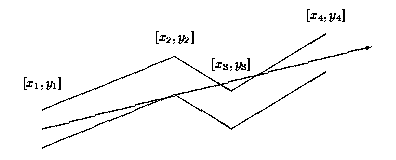
Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find, for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent points and the bent points do not stop the light beam.

Input

The input file contains several blocks each describing one pipe component. Each block starts with the number of bent points 2 <= n <= 20 on separate line. Each of the next n lines contains a pair of real values xi, yi separated by space. The last block is denoted with n = 0.

Output

The output file contains lines corresponding to blocks in input file. To each block in the input file there is one line in the output file. Each such line contains either a real value, written with precision of two decimal places, or the message Through all the pipe.. The real value is the desired maximal x-coordinate of the point where the light can reach from the source for corresponding pipe component. If this value equals to xn, then the message Through all the pipe. will appear in the output file.

Sample Input

4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0

Sample Output

4.67
Through all the pipe.

Source

Central Europe 1995

题意：

给n个点 构成两条平行的折线

问从管道口出发的光线最远能到达的横坐标

思路：

最远的光线一定是贴着管道的某两个端点走的

现在枚举这两个端点  判断其与后面折线的交点

刚开始没想到判断交点时 可以先判断line 和 line(up[k], down[k])

这样得到的k就是最小的不能达到的k

用这个k就可以拿来算line 和 line(up[k-1], up[k])以及line(down[k -1], down[k])的交点了

 //#include <bits/stdc++.h>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<stdio.h>
 #include<cstring>

 using namespace std;
 typedef long long int LL;

 #define zero(x) (((x) > 0? (x) : -(x)) < eps)
 const double eps = 1e-;
 int sgn(double x)
 {
     if(fabs(x) < eps) return ;
     if(x < ) return -;
     else return ;
 }

 struct point{
     double x, y;
     point(){}
     point(double _x, double _y)
     {
         x = _x;
         y = _y;
     }
     point operator -(const point &b)const
     {
         return point(x - b.x, y - b.y);
     }
     double operator ^(const point &b)const
     {
         return x * b.y - y * b.x;
     }
     double operator *(const point &b)const
     {
         return x * b.x + y * b.y;
     }
     void input()
     {
         scanf("%lf%lf", &x, &y);
     }
 };

 struct line{
     point s, e;
     line(){}
     line(point _s, point _e)
     {
         s = _s;
         e = _e;
     }
     //0表示直线重合，1表示平行，2相交
     pair<int, point>operator &(const line &b)const
     {
         point res = s;
         if(sgn((s - e) ^ (b.s - b.e)) == ){
             if(sgn((s - b.e) ^ (b.s - b.e)) == ){
                 return make_pair(, res);
             }
             else return make_pair(, res);
         }
         double t = ((s - b.s) ^ (b.s - b.e)) / ((s - e) ^ (b.s - b.e));
         res.x += (e.x - s.x) * t;
         res.y += (e.y - s.y) * t;
         return make_pair(, res);
     }
 };

 //判断直线与线段相交
 bool seg_inter_line(line l1, line l2)
 {
     return sgn((l2.s - l1.e) ^ (l1.s - l1.e)) * sgn((l2.e - l1.e) ^ (l1.s - l1.e)) <= ;
 }

 int n;
 point up[], down[];
 int main()
 {
     while(scanf("%d", &n) != EOF && n != ){
         for(int i = ; i < n; i++){
             up[i].input();
             down[i].x = up[i].x;
             down[i].y = up[i].y - 1.0;
         }

         bool flag = false;
         double ans = -100000000.0;
         int k;
         for(int i = ; i < n; i++){
             for(int j = i + ; j < n; j++){
                 for(k = ; k < n; k++){
                     if(seg_inter_line(line(up[i], down[j]), line(up[k], down[k])) == ){
                         break;
                     }
                 }
                 if(k >= n){
                     flag = true;
                     break;
                 }
                 if(k > max(i, j)){
                     if(seg_inter_line(line(up[i], down[j]), line(up[k - ], up[k]))){
                         pair<int, point>pr = line(up[i], down[j]) & line(up[k - ], up[k]);
                         point p = pr.second;
                         ans = max(ans, p.x);
                     }
                     if(seg_inter_line(line(up[i], down[j]), line(down[k - ], down[k]))){
                         pair<int, point>pr = line(up[i], down[j]) & line(down[k - ], down[k]);
                         point p = pr.second;
                         ans = max(ans, p.x);
                     }
                 }

                 for(k = ; k < n; k++){
                     if(seg_inter_line(line(down[i], up[j]), line(up[k], down[k])) == ){
                         break;
                     }
                 }
                 if(k >= n){
                     flag = true;
                     break;
                 }
                 if(k > max(i, j)){
                     if(seg_inter_line(line(down[i], up[j]), line(up[k - ], up[k]))){
                         pair<int, point>pr = line(down[i], up[j]) & line(up[k - ], up[k]);
                         point p = pr.second;
                         ans = max(ans, p.x);
                     }
                     if(seg_inter_line(line(down[i], up[j]), line(down[k - ], down[k]))){
                         pair<int, point>pr = line(down[i], up[j]) & line(down[k - ], down[k]);
                         point p = pr.second;
                         ans = max(ans, p.x);
                     }
                 }
             }
             if(flag){
                 break;
             }
         }
         //cout<<ans<<endl;
         if(flag){
             printf("Through all the pipe.\n");
         }
         else{
             printf("%.2f\n", ans);
         }
     }
     return ;
 }