接雨水12 · Trapping Rain Water12

［抄题］：

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

[暴力解法]：

时间分析：

空间分析：

［思维问题］：

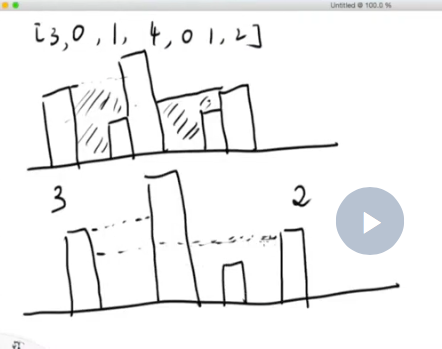
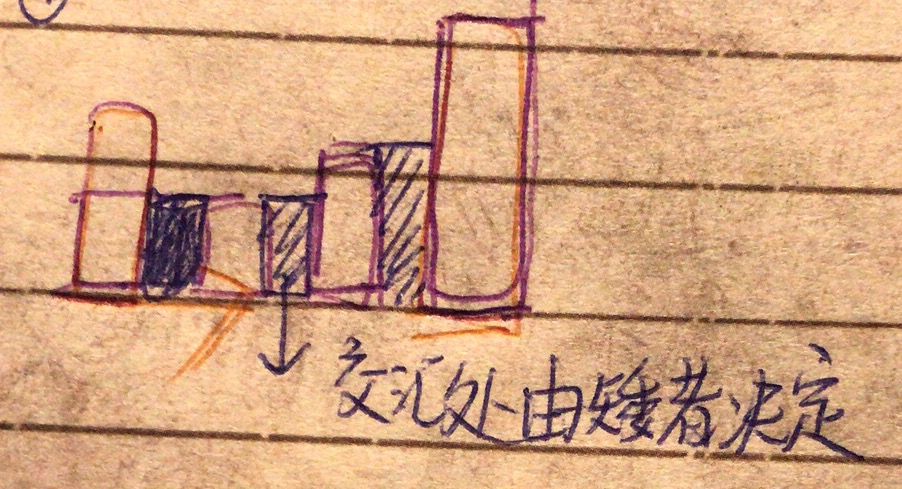
1. 灌水的多少基本上由左右边界中较矮的一块木板开始，由相邻是否有较高的木板决定。第一次学灌水，算了

［一句话思路］：

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

灌水的多少基本上由左右边界的木板决定。

［一刷］：

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

［复杂度］：Time complexity: O(n) Space complexity: O(n)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

［关键模板化代码］：

while (left < right) {
            if (heights[left] < heights[right]) {
                //start from left
                left++;
                if (left_max > heights[left]) {
                    result += (left_max - heights[left]);
                }else {
                    left_max = heights[left];
                }
            }else {
                //start from right
                right--;
                if (right_max > heights[right]) {
                    result += (right_max - heights[right]);
                }else {
                    right_max = heights[right];
                }
            }
        }

while (left < right)的基础上才能循环

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

装最多水的容器 · Container With Most Water 2指针

[代码风格] ：

public class Solution {
    /**
     * @param heights: a list of integers
     * @return: a integer
     */
    public int trapRainWater(int[] heights) {
        int result = 0;
        //corner case
        if (heights == null || heights.length == 0) {
            return 0;
        }

        int left = 0;
        int right = heights.length - 1;
        int left_max = heights[left];
        int right_max = heights[right];

        while (left < right) {
            if (heights[left] < heights[right]) {
                //start from left
                left++;
                if (left_max > heights[left]) {
                    result += (left_max - heights[left]);
                }else {
                    left_max = heights[left];
                }
            }else {
                //start from right
                right--;
                if (right_max > heights[right]) {
                    result += (right_max - heights[right]);
                }else {
                    right_max = heights[right];
                }
            }
        }
        return result;
    }
}

［抄题］：

Given n x m non-negative integers representing an elevation map 2d where the area of each cell is 1 x 1, compute how much water it is able to trap after raining.

Given 5*4 matrix

[12,13,0,12]
[13,4,13,12]
[13,8,10,12]
[12,13,12,12]
[13,13,13,13]

return 14.

[暴力解法]：

时间分析：

空间分析：

［思维问题］：

1. 以为从四个角当作外围，朝中间过渡。应该把四堵墙当作外围，要能把中间都包起来才能做外围。
2. 怎么想不到利用堆，要分析数据特点再选数据结构 而不是一个个套用数据结构：每次都是从q的顶点（最矮的点）从低往高注水，故用heap.
   1. 　　q中放的是能向四周扩展的cell, 但是每次都是从q的顶点（最矮的点）从低往高注水。不是从高往低duang地一下往下倒，没想象出来。

［一句话思路］：

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

［一刷］：

1. PQ的括号里要传新建的引用new CellComparator()，体现参数的多态
2. q中没有cell并往里头放时，新建即可
3. 队列已经创建出对象，则不用null。再判断对象是否为零，因此用isempty()
4. 从0 开始，取m个数，最后一个应该是m - 1，老是稍微理解了然后又忘了
5. java int[] 未初始化时默认值是，integer[]未初始化时默认值是null
6. int[][] visit = new int[n][m]; 已经忘写好几次了

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

灌水（扩展类）本质还是BFS，区区几个算法中的一种。要分析数据特点再选数据结构 而不是一个个套用数据结构

［复杂度］：Time complexity: O(m*n个元素*lg(m+n)每个元素在heap中取最小值) Space complexity: O(m*n个点保存在去重矩阵中)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

1. BFS，“扩展类”问题就应该想到，印象还不够深
2. dp好用，可不要贪杯哦
3. 重写@override是子类对父类的允许访问的方法的实现过程进行重新编写, 返回值和形参都不能改变。重载(overloading) 是在一个类里面，方法名字相同，而参数不同。

［关键模板化代码］：

class CellComparator implements Comparator<Cell> {
    public int compare(Cell a, Cell b) {
        if (a.h > b.h) {
            return 1;
        }else if (a.h == b.h) {
            return 0;
        }else {
            return -1;
        }
    }
}

自制CellComparator

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

542. 01 Matrix 所有点，用dfs

279. Perfect Squares dp

529. Minesweeper 扫雷 DFS BFS无疑了

[代码风格] ：

class Cell {
    int x, y, h;
    Cell (int xx, int yy, int hh) {
        x = xx;
        y = yy;
        h = hh;
    }
}

class CellComparator implements Comparator<Cell> {
    public int compare(Cell a, Cell b) {
        if (a.h > b.h) {
            return 1;
        }else if (a.h == b.h) {
            return 0;
        }else {
            return -1;
        }
    }
}

public class Solution {
    /**
     * @param heights: a matrix of integers
     * @return: an integer
     */
    public int trapRainWater(int[][] heightMap) {
        int result = 0;
        int n = heightMap.length;
        int m = heightMap[0].length;
        int[][] visit = new int[n][m];
        int[] dx = {0, 1, 0, -1};
        int[] dy = {1, 0, -1, 0};
        //corner case
        if (heightMap == null || m == 0 || n == 0) {
            return 0;
        }
        PriorityQueue<Cell> q = new PriorityQueue<>(new CellComparator());
        //get 4 edges into q
        for (int i = 0; i < n; i++) {
            q.offer(new Cell(i, 0, heightMap[i][0]));
            q.offer(new Cell(i, m - 1, heightMap[i][m - 1]));
            visit[i][0] = 1;
            visit[i][m - 1] = 1;
        }
        for (int j = 0; j < m; j++) {
            q.offer(new Cell(0, j, heightMap[0][j]));
            q.offer(new Cell(n - 1, j, heightMap[n - 1][j]));
            visit[0][j] = 1;
            visit[n - 1][j] = 1;
        }
        //bfs
        while (!q.isEmpty()) {
            Cell now = q.poll();
            int cx = now.x;
            int cy = now.y;

            for (int i = 0; i < 4; i++) {
                int nx = cx + dx[i];
                int ny = cy + dy[i];

                if (0 <= nx && nx < n && 0 <= ny && ny < m &&
                visit[nx][ny] == 0) {
                    visit[nx][ny] = 1;
                    q.offer(new Cell(nx, ny, Math.max(now.h, heightMap[nx][ny])));
                    result += Math.max(0, now.h - heightMap[nx][ny]);
                }
            }
        }

        return result;
    }
}