【动态规划】bzoj2298: [HAOI2011]problem a

建模超级妙……

Description

一次考试共有n个人参加，第i个人说：“有ai个人分数比我高，bi个人分数比我低。”问最少有几个人没有说真话(可能有相同的分数)

Input

第一行一个整数n，接下来n行每行两个整数，第i+1行的两个整数分别代表ai、bi

Output

一个整数，表示最少有几个人说谎

Sample Input

3
2 0
0 2
2 2

Sample Output

1

HINT

100%的数据满足： 1≤n≤100000   0≤ai、bi≤n

---

题目分析

一开始真的真的没看出来是个dp……

口胡做法

口胡了一个做法：给每一个人确定一个排名（若分数相同那么排名相同），然后用一些神奇的方法去考虑这些排名是否不互相矛盾。还考虑了一下不矛盾性可不可以递移（最近学了tarjan所以看什么都是图论）……然而发现并不可做。

正经做法

如果考虑分数相同的问题，那么每一个人的排名其实可以看做一个区间$[l,r]=[a_i+1,n-b_i]$。首先考虑哪些话必假：1.$l>r$；2.排名区间为$[l,r]$的个数大于$r-l+1$，此时$[l,r]$只能有$r-l+1$个。又因为答案不要求输出方案，所以只需要取够$r-l+1$就行了，而不用管到底取了哪些区间。

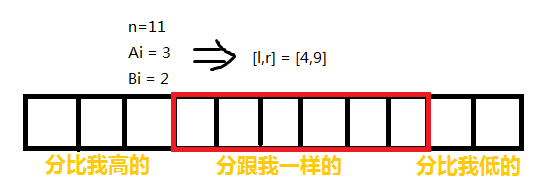
把每一个人都映射成区间之后，我们来观察一下很多相同区间的情况。也就是说，有很多人的排名相同的情况。

可以发现他们是互不影响的。比如我说我排名是$[1,5]$里的，你说你也是$[1,5]$里的，那么我和你的话是不冲突的。可以同时认定我们说的话是真话并且对于其他的选择来说没有干扰————既然这样，何不把$v$个区间$[l,r]$再次映射成一条有权值$v$的线段呢？这里线段的权值代表：认同“$[l,r]$这段区间里的人分数相同”是真话所能够获得的人数。

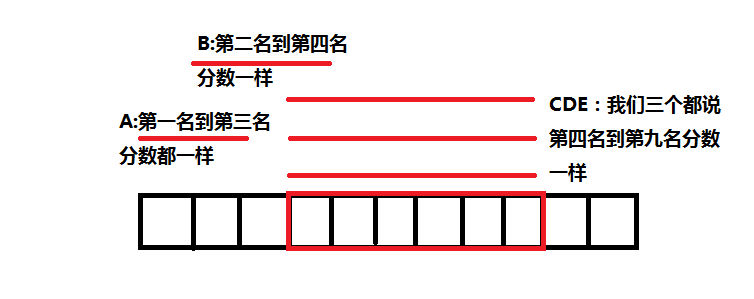
于是问题就转化为了：

有若干条带权值的线段$[l,r]$，要求选出互不重叠的一些，使得所选线段权值和最大。

这样就是dp问题了。

正经做法的疑问？

但是这样如何能够保证：选了的$[l,r]$是合法的？

换而言之，“$[l,r]$这段区间里的人分数相同”这句话如果要成立，那么不仅仅是要求有那么一两个人说自己在这个区间里，还要求总共有$r-l+1$个人都是在这个区间里。

嘛，我们还有那些说假话的人么。所以只要把他们安排在需要人的地方就行了。

但是如何保证说假话的人足够多，以至于能够满足我们钦定的真话呢？

这样想似乎非常抽象并且非常复杂，但实际上形象一点理解就很自然了。这里陈述两个基本事实：

1. 每一个人无论说了真话还是假话最终都会有一个排名
2. 每一个人说的话占的排名最多长度为$n$

那么所有钦定的真话最长也就只有$n$，因为钦定的话不会互相重叠。又因为说话的人自己会算作一次，所以一定是够填的。

注意

还有注意就是，那个dp时候用的是$lower\_bound$……突然脑抽用了$upper\_bound-1$发现只有90……

 #include<bits/stdc++.h>
 typedef std::pair<int, int> pr;
 const int maxn = ;

 struct seg
 {
     int l,r,v;
     bool operator < (seg a) const
     {
         return r < a.r;
     }
     seg(int a=, int b=, int c=):l(a),r(b),v(c) {}
 }a[maxn];
 int n,f[maxn],d[maxn],tot;
 std::map<pr, int> mp;

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 int main()
 {
     n = read();
     for (int i=; i<=n; i++)
     {
         int ax = read(), bx = read();
         int l = ax+, r = n-bx;
         if (l > r) continue;
         pr tt = std::make_pair(l, r);
         if (mp[tt]==r-l+) continue;
         if (!mp[tt])
             a[++tot] = seg(l, r, );
         mp[tt]++;
     }
     for (int i=; i<=tot; i++)
         a[i] = seg(a[i].l, a[i].r, mp[std::make_pair(a[i].l, a[i].r)]);
     std::sort(a+, a+tot+);
     for (int i=; i<=tot; i++) d[i] = a[i].r;
     for (int i=; i<=tot; i++)
     {
         int tt = std::lower_bound(d+, d+i, a[i].l)-d-;
         f[i] = std::max(f[i-], f[tt]+a[i].v);
     }
     printf("%d\n",n-f[tot]);
     return ;
 }