Sudoku POJ - 3076

Sudoku

Time Limit: 10000MS		Memory Limit: 65536K
Total Submissions: 5769		Accepted: 2684

Description

A Sudoku grid is a 16x16 grid of cells grouped in sixteen 4x4 squares, where some cells are filled with letters from A to P (the first 16 capital letters of the English alphabet), as shown in figure 1a. The game is to fill all the empty grid cells with letters from A to P such that each letter from the grid occurs once only in the line, the column, and the 4x4 square it occupies. The initial content of the grid satisfies the constraints mentioned above and guarantees a unique solution. 
 
Write a Sudoku playing program that reads data sets from a text file.

Input

Each data set encodes a grid and contains 16 strings on 16 consecutive lines as shown in figure 2. The i-th string stands for the i-th line of the grid, is 16 characters long, and starts from the first position of the line. String characters are from the set {A,B,…,P,-}, where – (minus) designates empty grid cells. The data sets are separated by single empty lines and terminate with an end of file.

Output

The program prints the solution of the input encoded grids in the same format and order as used for input.

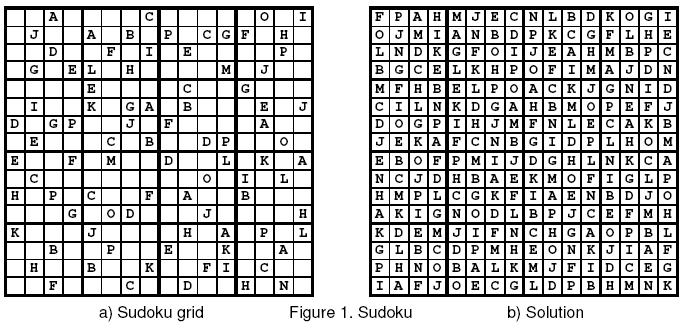
Sample Input

--A----C-----O-I
-J--A-B-P-CGF-H-
--D--F-I-E----P-
-G-EL-H----M-J--
----E----C--G---
-I--K-GA-B---E-J
D-GP--J-F----A--
-E---C-B--DP--O-
E--F-M--D--L-K-A
-C--------O-I-L-
H-P-C--F-A--B---
---G-OD---J----H
K---J----H-A-P-L
--B--P--E--K--A-
-H--B--K--FI-C--
--F---C--D--H-N-

Sample Output

FPAHMJECNLBDKOGI
OJMIANBDPKCGFLHE
LNDKGFOIJEAHMBPC
BGCELKHPOFIMAJDN
MFHBELPOACKJGNID
CILNKDGAHBMOPEFJ
DOGPIHJMFNLECAKB
JEKAFCNBGIDPLHOM
EBOFPMIJDGHLNKCA
NCJDHBAEKMOFIGLP
HMPLCGKFIAENBDJO
AKIGNODLBPJCEFMH
KDEMJIFNCHGAOPBL
GLBCDPMHEONKJIAF
PHNOBALKMJFIDCEG
IAFJOECGLDPBHMNK

Source

Southeastern Europe 2006

这个就是2676变了一下形

直接上代码了

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#include <bitset>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define rb(a) scanf("%lf", &a)
#define rf(a) scanf("%f", &a)
#define pd(a) printf("%d\n", a)
#define plld(a) printf("%lld\n", a)
#define pc(a) printf("%c\n", a)
#define ps(a) printf("%s\n", a)
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , INF = 0x7fffffff;
int S[maxn], head[maxn], vis[maxn];
int U[maxn], D[maxn], L[maxn], R[maxn];
int C[maxn], X[maxn];
int n, m, ans, ret, ans1;

void init()
{
    for(int i = ; i <= m; i++)
        D[i] = i, U[i] = i, R[i] = i + , L[i] = i - ;
    L[] = m, R[m] = ;
    mem(S, ), mem(head, -);
    ans = m + ;
}

void delc(int c)
{
    L[R[c]] = L[c], R[L[c]] = R[c];
    for(int i = D[c]; i != c; i = D[i])
        for(int j = R[i]; j != i; j = R[j])
            U[D[j]] = U[j], D[U[j]] = D[j], S[C[j]]--;

}

void resc(int c)
{
    for(int i = U[c]; i != c; i = U[i])
        for(int j = L[i]; j != i; j = L[j])
            U[D[j]] = j, D[U[j]] = j, S[C[j]]++;
    L[R[c]] = c, R[L[c]] = c;
}

void add(int r, int c)
{
    ans++, S[c]++, C[ans] = c, X[ans] = r;
    D[ans] = D[c];
    U[ans] = c;
    U[D[c]] = ans;
    D[c] = ans;
    if(head[r] < ) head[r] = L[ans] = R[ans] = ans;
    else L[ans] = head[r], R[ans] = R[head[r]],L[R[head[r]]] = ans, R[head[r]] = ans;
}

bool dfs(int sh)
{
    if(!R[])
    {
        sort(vis, vis +  * );
        int cnt = ;
        for(int i = ; i < ; i++)
        {
            for(int j = ; j < ; j++)
            {
                int num = vis[cnt++];

                num=num - (i *  + j) * ;
                printf("%c", 'A' + num - );
               // cout << 111 << endl;

            }
            printf("\n");
        }
        printf("\n");

        return true;
    }
    int c = R[];
    for(int i = R[]; i; i = R[i]) if(S[c] > S[i]) c = i;
    delc(c);
    for(int i = D[c]; i != c; i = D[i])
    {
        vis[sh] = X[i];
        for(int j = R[i]; j != i; j = R[j])
            delc(C[j]);
        if(dfs(sh + )) return true;
        for(int j = L[i]; j != i; j = L[j])
            resc(C[j]);
    }
    resc(c);
    return false;
}

char str[][];

void build(int x, int y, int k)
{
    ans1 = (x *  + y - ) *  + k;
    add(ans1, x *  + k);
    add(ans1,  *  + (y - ) *  + k);
    add(ans1,  *  *  + x *  + y);
    int block = (y - ) /  *  + x / ;
    add(ans1,  *  *  + block *  + k);

}

int main()
{

    while(~scanf("%s", str[]))
    {
        m =  *  * ;
        init();

        for(int i = ; i < ; i++)
        {
            rs(str[i]);
        }
        for(int i = ; i < ; i++)
            for(int j = ; j <= ; j++)
            {
                if(str[i][j - ] == '-')
                    for(int k = ; k <= ; k++) build(i, j, k);
                else
                    build(i, j, str[i][j - ] - ('A' - ));
            }
        dfs();
    }

    return ;
}