数据结构【查找】—平衡二叉树AVL

/*自己看了半天也没看懂代码，下次再补充说明*/

解释：

　　平衡二叉树（Self-Balancing Binary Search Tree 或Height-Balanced Binary Search Tree），是一种二叉排序树，其中每一个节点的左子树和右子树的高度差至多等于1。

实现原理：

　　平衡二叉树构建的基本思想就是在构建二又排序树的过程中，每当插入一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树。在保持二又排序树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。

右旋：

　　

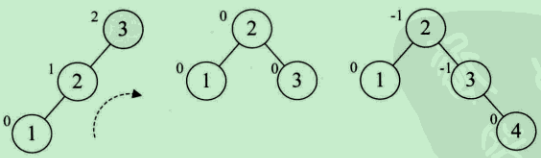
左旋：

　　

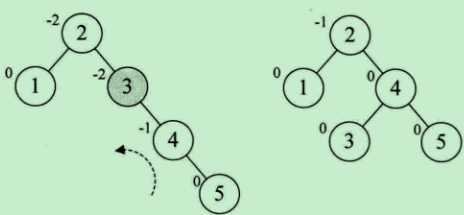
左旋、右旋：

　　

代码实现：

　　

 #include "000库函数.h"

 #define MAXSIZE 100//
 #define EH 0
 #define LH +1  //左高
 #define RH -1  //右高  

 //二叉树的结构
 struct BiTree
 {
     int data;
     int bf;//AVL的平衡因子
     BiTree *lchild, *rchild;
 };

 bool L_Rotate(BiTree* &T) {//对T的左子树作左旋平衡处理
     BiTree *R;
     R = T->rchild;
     T->rchild = R->lchild;//R的左子树挂接为T的右子树
     R->lchild = T;
     T = R;
     return true;
 }

 bool R_Rotate(BiTree* &T) {//对T做右旋处理
     BiTree *L;
     L = T->lchild;
     T->lchild = L->rchild;
     L->rchild = T;
     T = L;
     return true;
 }

 //判断再加入左子树会不会打破平衡
 bool LeftBalace(BiTree* &T) {//如今再添加进左边就应该添加后判断是否打破了平衡
     BiTree *L, *Lr;
     L = T->lchild;
     switch (L->bf)//判断左子树的平衡因子
     {
     case LH://原为左增，现再增加就打破平衡了,故需要做右旋处理
         T->bf = L->bf = EH;
         R_Rotate(T);
         break;
     case RH://原节点为右增，再增加左节点（深度+1），就打破平衡了，故作双旋处理
         Lr = L->rchild;
         switch (Lr->bf)
         {
         case LH:
             T->bf = RH;
             L->bf = EH;
             break;
         case EH:
             T->bf = L->bf = EH;
             break;
         case RH:
             T->bf = EH;
             L->bf = LH;
             break;
         default:
             break;
         }
         Lr->bf = EH;
         L_Rotate(T->lchild);//对T的左子树作左旋平衡处理
         R_Rotate(T);//对T做右旋处理
         break;
     default:
         break;
     }
     return true;
 }

 //判断再加入右子树会不会打破平衡
 bool RightBalace(BiTree* &T) {//如今再添加进右边就应该添加后判断是否打破了平衡
     BiTree *R, *Rl;
     R = T->rchild;
     switch (R->bf)//判断右子树的平衡因子
     {
     case LH://原节点为左增，再增加右节点（深度+1），就打破平衡了，故作双旋处理
         Rl = R->lchild;
         switch (Rl->bf)
         {
         case LH:
             T->bf = EH;
             R->bf = RH;
             break;
         case EH:
             T->bf = R->bf = EH;
             break;
         case RH:
             T->bf = LH;
             R->bf = EH;
             break;
         default:
             break;
         }
         Rl->bf = EH;
         R_Rotate(T->rchild);//对T的左子树作左旋平衡处理
         L_Rotate(T);//对T做右旋处理
         break;
     case RH://原为右增，现再增加就打破平衡了,故需要做左旋处理
         T->bf = R->bf = EH;
         L_Rotate(T);
         break;
     default:
         break;
     }
     return true;
 }

 //AVL创建
 /*  若在平衡的二叉排序树T中不存在和e有相同关键字的结点，则插入一个 */
 /*  数据元素为e的新结点，并返回1，否则返回0。若因插入而使二叉排序树 */
 /*  失去平衡，则作平衡旋转处理，布尔变量taller反映T长高与否。 */
 bool InsertAVL(BiTree * &T, int elem, bool &n) {
     if (T == NULL) {
         BiTree *p;
         p = new BiTree;
         p->data = elem;
         p->bf = EH;
         p->lchild = NULL;
         p->rchild = NULL;
         T = p;
         n = true;
         return true;
     }
     if (T->data == elem) {//数据已存在，不需要再添加
         n = false;
         return false;
     }
     if (elem < T->data) {
         if (!(InsertAVL(T->lchild, elem, n)))//应当继续在左子树中继续查找
             return false;//添加失败
         if (n) {//添加成功
             switch (T->bf)//检查AVL的平衡因子
             {
             case LH://原树左边高
                 LeftBalace(T);//如今再添加进左边就应该添加后判断是否打破了平衡
                 n = false;
                 break;
             case EH://原树左等高度,那就加入其左边，让其增高
                 T->bf = LH;
                 n = true;
                 break;
             case RH://原树右端高，那就加入左端，抵消有右边的高度
                 T->bf = EH;
                 n = false;
                 break;
             default:
                 break;
             }
         }
     }
     else {
         if (!(InsertAVL(T->rchild, elem, n)))//应当继续在右子树中继续查找
             return false;//添加失败
         if (n) {//添加成功
             switch (T->bf)//检查AVL的平衡因子
             {
             case LH://原树左边高
                 T->bf = EH;//加入右端，抵消有左边的高度
                 n = false;
                 break;
             case EH://原树左等高度,那就加入其右边，让其增高
                 T->bf = LH;
                 n = true;
                 break;
             case RH://原树右端高
                 RightBalace(T);//如今再添加进右边就应该添加后判断是否打破了平衡
                 n = false;
                 break;
             default:
                 break;
             }
         }
     }

 }
 //遍历AVL
 void ShowTree(BiTree *T) {
     //进行中序浏览
     if (T) {
         ShowTree(T->lchild);
         cout << T->data << "—>";
         ShowTree(T->rchild);
     }
 }

 int T033(void)
 {
     int i;
     int a[] = { ,,,,,,,,, };
     BiTree *T = new BiTree;
     T = NULL;
     bool taller;//用来判断AVL是否增加了深度
     BiTree *p;
     for (i = ; i < ; i++)    {
         InsertAVL(T, a[i], taller);
         if (i == )p = T;//记住头结点
     }
     ShowTree(T);
     cout << endl;
     return ;
 }