Solution -「POI 2013」LAB-Maze

\(\mathscr{Description}\)

  Link.

  构造一个边平行与坐标轴, 顶点是整点, 相邻边互相垂直, 且逆时针遍历顶点时转向 (向左或向右) 符合给定字符串的不自交多边形.

  顶点数 \(n\le10^5\).

\(\mathscr{Solution}\)

  设 \(L\) 为左转数, \(R\) 为右转数, 显然, 有解的必要条件是 \(L-R=4\), 不然不可能逆时针转回起点.

  接下来, 注意到相邻的一对 LR 或者 RL 一定体现为一个 "Z" 字形, 并不影响边的走向. 因此, 可以尝试通过不断去除这样的字符对来递归构造多边形.

  研究递归的过程. 递归尽头一定是 LLLL, 此时我们新建一个矩形. 在回溯过程中, 我们要做的工作就是在一条直线中插入一个 "Z", 并合理调整坐标关系. 如图:

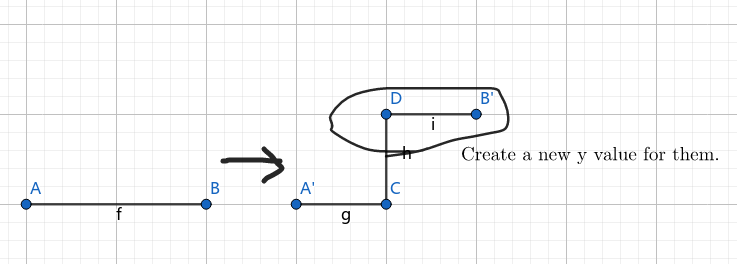
  说着很简单, 怎么实现呢?

  对于 LR 对的寻找, 可以用双向连边维护字符串上剩余字符的相邻关系, 然后把所有可能的 LR 和 RL 丢到队列里. 删掉 LR 之后再顺便检查一下新挨在一起的字符是否是 LR 或 RL.

  对于 "合理调整坐标关系", 最好的安排方式自然是把 "Z" 的一竖变得 "很短很短", 短到不可能碰到任何其他边. 当然, 因为坐标需要是整数, 这不太可能. 不过, 我们在构造过程中并不关心一个点的具体坐标, 因而, 可以用两个双向链表维护 \(x\) 轴和 \(y\) 轴, 每个点的坐标仅仅用指向链表中元素的两个指针描述. 插入坐标通过链表插入 \(\mathcal O(1)\) 实现, 由于共用一个坐标的点一定只有两个, 所以也很容易将一个坐标 "分裂" 成两个相近坐标.

  当然, 如果真的要写链表, 就需要精细地去记录当前直线的走向, 否则难以通过迭代器的关系判断左右上下. 一个懒人方法是用 Splay 维护坐标轴, 原理一样, 不过就可以直接用 rank 来描述两个坐标的相对关系啦. 取决于实现方式, 复杂度为 \(\mathcal O(n)\) 或者 \(\mathcal O(n\log n)\).

\(\mathscr{Code}\)

/*+Rainybunny+*/

#include <bits/stdc++.h>

#define rep(i, l, r) for (int i = l, rep##i = r; i <= rep##i; ++i)
#define per(i, r, l) for (int i = r, per##i = l; i >= per##i; --i)

const int MAXN = 1e5;
int n, pre[MAXN + 5], suf[MAXN + 5], xid[MAXN + 5], yid[MAXN + 5];
char tur[MAXN + 5];
bool vis[MAXN + 5];
std::queue<int> gap;

struct Splay {
    static const int MAXND = 3e5;
    int node, root, ch[MAXND][2], siz[MAXND], fa[MAXND], lab[MAXND];

    Splay() {
        newnd(), newnd(), root = fa[ch[1][1] = 2] = 1, siz[1] = 2;
    }

    inline int newnd() {
        return siz[++node] = 1, node;
    }

    inline void pushup(const int u) {
        siz[u] = siz[ch[u][0]] + siz[ch[u][1]] + 1;
    }

    inline void rotate(const int u) {
        int v = fa[u], w = fa[v], k = ch[v][1] == u;
        if ((fa[u] = w)) ch[w][ch[w][1] == v] = u;
        if ((ch[v][k] = ch[u][!k])) fa[ch[v][k]] = v;
        pushup(ch[fa[v] = u][!k] = v), pushup(u);
    }

    inline void splay(const int u, const int tar) {
        for (int v, w; (v = fa[u]) != tar; rotate(u)) {
            if ((w = fa[v]) != tar) {
                rotate((v == ch[w][0]) == (u == ch[v][0]) ? v : u);
            }
        }
        if (!tar) root = u;
    }

    inline int rank(const int u) {
        splay(u, 0);
        return siz[ch[u][0]] + 1;
    }

    inline int kth(int k) {
        int u = root;
        while (true) {
            if (k <= siz[ch[u][0]]) u = ch[u][0];
            else if (!(k -= siz[ch[u][0]] + 1)) return u;
            else u = ch[u][1];
        }
    }

    /** insert a node s.t. the rank of it is @p rk */
    inline int insertAs(const int rk) {
        assert(1 < rk && rk <= siz[root]);
        int u = kth(rk - 1), v = kth(rk);
        splay(u, 0), splay(v, u), assert(!ch[v][0]);
        fa[ch[v][0] = newnd()] = v, pushup(v), pushup(u);
        return ch[v][0];
    }

    inline void relable(const int u) {
        if (!u) return ;
        relable(ch[u][0]), lab[u] = ++lab[0], relable(ch[u][1]);
    }
} X, Y;

inline void solve() {
    if (gap.empty()) {
        std::vector<int> rest;
        rep (i, 0, n - 1) if (!vis[i]) rest.push_back(i);
        assert(rest.size() == 4); // As a rectangle.
        X.insertAs(2), X.insertAs(3);
        Y.insertAs(2), Y.insertAs(3);
        rep (i, 0, 3) {
            xid[rest[i]] = !i || i == 3 ? 3 : 4;
            yid[rest[i]] = i < 2 ? 3 : 4;
        }
        // printf("%d %d %d %d\n", rest[0], rest[1], rest[2], rest[3]);
        return ;
    }

    int p = gap.front(), q = suf[p], s = pre[p], t = suf[q];
    gap.pop();
    if (vis[p] || vis[q] || tur[p] == tur[q]) return solve();
    vis[p] = vis[q] = true, suf[s] = suf[q], pre[t] = pre[p];
    assert(!vis[s] && !vis[t]);
    if (tur[s] != tur[t]) gap.push(s);
    solve();
    // printf("%d --> %d - %d <-- %d\n", s, p, q, t);

    if (yid[s] == yid[t]) {
        int sxr = X.rank(xid[s]), txr = X.rank(xid[t]);
        xid[p] = xid[q] = X.insertAs(std::min(sxr, txr) + 1);
        yid[p] = yid[s];
        if ((tur[p] == 'L') == (sxr < txr)) {
            yid[q] = yid[t] = Y.insertAs(Y.rank(yid[p]) + 1);
        } else {
            yid[q] = yid[t] = Y.insertAs(Y.rank(yid[p]));
        }
    } else {
        int syr = Y.rank(yid[s]), tyr = Y.rank(yid[t]);
        yid[p] = yid[q] = Y.insertAs(std::min(syr, tyr) + 1);
        xid[p] = xid[s];
        if ((tur[p] == 'R') == (syr < tyr)) {
            xid[q] = xid[t] = X.insertAs(X.rank(xid[p]) + 1);
        } else {
            xid[q] = xid[t] = X.insertAs(X.rank(xid[p]));
        }
    }
}

int main() {
    // freopen("test.in", "r", stdin);
    // freopen("test.out", "w", stdout);

    scanf("%s", tur), n = strlen(tur);
    std::replace(tur, tur + n, 'P', 'R'); // No Polish :(

    int dlt = 0;
    rep (i, 0, n - 1) dlt += tur[i] == 'L' ? 1 : -1;
    if (dlt != 4) return puts("NIE"), 0;

    rep (i, 0, n - 1) {
        pre[i] = (i + n - 1) % n, suf[i] = (i + 1) % n;
        if (tur[i] != tur[(i + 1) % n]) gap.push(i);
    }

    solve();
    X.relable(X.root), Y.relable(Y.root);
    rep (i, 0, n - 1) printf("%d %d\n", X.lab[xid[i]], Y.lab[yid[i]]);
    return 0;
}

  顺便, 给出自己码的一个 SPJ.

/*+Rainybunny+*/

#include "testlib.h"
#include <bits/stdc++.h>

#define MSG_OK \
    "Congratulations~"
#define MSG_SOLUTION_EXISTS \
    "You don't find a solution, but jury does."
#define MSG_NOT_PARALLEL \
    "An edge isn't parallel to x-axis or y-axis (%d-th edge, 0-indexed)."
#define MSG_POINT_COINCIDE \
    "Two nodes coincide in your solution."
#define MSG_NOT_VERTICAL \
    "Two neighboring edges aren't vertical in your solution (%d-th edge and " \
    "%d-th edges, 0-indexed)."
#define MSG_OUTSIDE_WALK \
    "You're walking outside of your polygon."
#define MSG_WRONG_TURNING \
    "A turning direction doesn't meet the requirement."
#define MSG_SELF_INTER \
    "The polygon is self-intersecting in your solution."

#define rep(i, l, r) for (int i = l, rep##i = r; i <= rep##i; ++i)
#define per(i, r, l) for (int i = r, per##i = l; i >= per##i; --i)

typedef long long LL;
typedef std::pair<int, int> PII;
#define fi first
#define se second

const int MAXN = 1e5;
int n;
std::string tur;

struct Point {
    int x, y;
    inline Point operator - (const Point& u) const {
        return { x - u.x, y - u.y };
    }
    inline LL operator * (const Point& u) const {
        return 1ll * x * u.x + 1ll * y * u.y;
    }
    inline LL operator ^ (const Point& u) const {
        return 1ll * x * u.y - 1ll * y * u.x;
    }
    inline bool operator < (const Point& u) const {
        return x == u.x ? y < u.y : x < u.x;
    }
};

Point pnt[MAXN + 5];

inline void initCheck() {
    tur = inf.readToken(), n = int(tur.size());
    std::rotate(tur.begin(), tur.end() - 1, tur.end());

    std::string your = ouf.readToken(), jury = ans.readToken();
    if (your == "NIE" && jury != "NIE") quitf(_wa, MSG_SOLUTION_EXISTS);
    else if (your == "NIE") quitf(_ok, MSG_OK);
    std::reverse(your.begin(), your.end());
    for (char c: your) ouf.unreadChar(c);

    rep (i, 0, n - 1) {
        pnt[i].x = ouf.readInt(-1e9, 1e9);
        pnt[i].y = ouf.readInt(-1e9, 1e9);
        // fprintf(stderr, "? %d %d\n", pnt[i].x, pnt[i].y);
    }
}

int fail[MAXN + 5];
std::string act;
std::set<Point> apr;

inline void turningCheck() {
    rep (i, 0, n - 1) {
        if ((pnt[i].x != pnt[(i + 1) % n].x)
          && (pnt[i].y != pnt[(i + 1) % n].y)) quitf(_wa, MSG_NOT_PARALLEL, i);
        if (apr.count(pnt[i])) quitf(_wa, MSG_POINT_COINCIDE);
        apr.insert(pnt[i]);

        Point p(pnt[i] - pnt[(i + n - 1) % n]), q(pnt[(i + 1) % n] - pnt[i]);
        // fprintf(stderr, "(%d,%d) -> (%d,%d)\n", p.x, p.y, q.x, q.y);
        if (p * q) quitf(_wa, MSG_NOT_VERTICAL, (i + n - 1) % n, i);
        act += (p ^ q) > 0 ? 'L' : 'P';
    }

    int dlt = 0;
    for (int c: act) dlt += c == 'L' ? 1 : -1;
    if (dlt == -4) {
        // In this case, the answer should be "NIE", but the checker won't
        // refuse to check your answer, knowing you must be wrong before.
        quitf(_wa, MSG_OUTSIDE_WALK);
    }
    // std::cerr << "Your turning token: " << act << '\n';

    fail[0] = -1;
    for (int i = 1, j = -1; i < n; ++i) {
        while (~j && tur[j + 1] != tur[i]) j = fail[j];
        fail[i] = j += tur[j + 1] == tur[i];
    }

    for (int i = 0, j = -1; i < 2 * n; ++i) {
        while (~j && tur[j + 1] != act[i % n]) j = fail[j];
        if ((j += tur[j + 1] == act[i % n]) == n - 1) return ;
    }
    quitf(_wa, MSG_WRONG_TURNING);
}

int mx, dc[MAXN + 5];
std::vector<PII> evt[MAXN + 5], req[MAXN + 5];
std::set<int> cut;

inline void selfInterCheck() {
    rep (i, 0, n - 1) dc[++mx] = pnt[i].x;
    std::sort(dc + 1, dc + mx + 1);
    mx = std::unique(dc + 1, dc + mx + 1) - dc - 1;
    rep (i, 0, n - 1) {
        pnt[i].x = std::lower_bound(dc + 1, dc + mx + 1, pnt[i].x) - dc;
    }

    rep (i, 0, n - 1) {
        if (pnt[i].x == pnt[(i + 1) % n].x) {
            int ya = pnt[i].y, yb = pnt[(i + 1) % n].y;
            if (ya > yb) std::swap(ya, yb);
            req[pnt[i].x].emplace_back(ya, yb);
        } else {
            int xa = pnt[i].x, xb = pnt[(i + 1) % n].x;
            if (xa > xb) std::swap(xa, xb);
            evt[xa].emplace_back(pnt[i].y, 1);
            evt[xb].emplace_back(pnt[i].y, 0);
        }
    }

    rep (i, 1, mx) {
        for (const PII& p: evt[i]) if (!p.se) cut.erase(p.fi);
        for (const PII& p: req[i]) {
            auto&& it = cut.upper_bound(p.se);
            if (it != cut.begin() && *--it >= p.fi) quitf(_wa, MSG_SELF_INTER);
        }

        for (const PII& p: evt[i]) if (p.se) {
            if (cut.count(p.fi)) quitf(_wa, MSG_SELF_INTER);
            cut.insert(p.fi);
        }

        for (const PII& p: evt[i]) if (!p.se) cut.insert(p.fi);
        for (const PII& p: req[i]) if (p.fi + 2 <= p.se) {
            auto&& it = cut.upper_bound(p.se - 1);
            if (it != cut.begin() && *--it > p.fi) quitf(_wa, MSG_SELF_INTER);
        }

        for (const PII& p: evt[i]) if (!p.se) cut.erase(p.fi);
    }
}

int main(int argc, char** argv) {
    registerTestlibCmd(argc, argv);

    initCheck();
    turningCheck();
    selfInterCheck();

    quitf(_ok, MSG_OK);
    return 0;
}